İstatistiklerdeki önem düzeyi, alınan (öngörülen) verilerin doğruluğu ve doğruluğundaki güven derecesini yansıtan önemli bir göstergedir. Konsept çeşitli alanlarda yaygın olarak kullanılmaktadır: sosyolojik araştırma yapmaktan, bilimsel hipotezlerin istatistiksel testine kadar.

tanım
İstatistiksel anlamlılık düzeyi (veya istatistiksel olarak anlamlı sonuç), çalışılan göstergelerin yanlışlıkla ortaya çıkma ihtimalinin ne olduğunu gösterir. Fenomenin genel istatistiksel önemi, katsayı p değeri (p düzeyi) ile ifade edilir. Herhangi bir deney veya gözlemde, elde edilen verilerin örnekleme hataları nedeniyle olması muhtemeldir. Bu, özellikle sosyoloji için geçerlidir.
Diğer bir deyişle, bir kaza sonucu oluşma olasılığı son derece küçük veya aşırı uçlara eğilimli olan bir istatistik önemlidir. Bu bağlamda aşırı, istatistiklerin boş hipotezden sapma derecesi olarak kabul edilir (elde edilen örnek verilerle tutarlılık için kontrol edilen bir hipotez). Bilimsel uygulamada, anlamlılık düzeyi veri toplamadan önce seçilmiştir ve bir kural olarak, katsayısı 0.05'tir (% 5). Doğru değerlerin son derece önemli olduğu sistemler için bu gösterge% 0.01 (% 1) veya daha az olabilir.
geçmiş
Anlamlılık düzeyi kavramı, 1925'te istatistiksel hipotezleri test etmek için bir metodoloji geliştirdiğinde İngiliz istatistikçi ve genetikçi Ronald Fisher tarafından tanıtıldı. Bir süreci analiz ederken, belirli olayların belirli bir olasılık var. "Hata hatası" kavramına giren küçük (veya belli olmayan) yüzde olasılıklarla çalışırken güçlükler ortaya çıkıyor.
Doğrulamak için yeterince spesifik olmayan istatistiklerle çalışırken, bilim insanları küçük miktarlarda “müdahale eden” boş hipotez sorunuyla karşı karşıya kaldılar. Fisher bu tür sistemler için tanımlamayı önerdi olayların olasılığı Hesaplamalardaki boş hipotezi reddetmenize izin veren uygun bir seçici dilim olarak% 5 (0.05).
Sabit bir katsayının getirilmesi
1933 yılında, bilim insanları Jerzy Neumann ve Egon Pearson, çalışmalarında önceden (veri toplanmadan önce) belirli bir önem seviyesi belirlemelerini tavsiye ettiler. Seçim sırasında bu kuralların kullanımına ilişkin örnekler açıkça görülmektedir. Biri çok popüler olan ve ikincisi pek az bilinen iki aday olduğunu varsayalım. Açıkçası, ilk aday seçimi kazanıyor ve ikincinin şansı sıfıra gidiyor. Gayret ediyorlar - ama eşit değil: her zaman mücbir sebep olasılığı, sansasyonel bilgiler, öngörülen seçim sonuçlarını değiştirebilecek beklenmedik kararlar vardır.
Neumann ve Pearson, Fisher'ın önerilen anlamlılık düzeyi 0,05'in (α simgesiyle gösterilen) en uygun olduğunu kabul etti. Ancak, 1956'da Fisher kendisi bu değerin tespitine karşı çıktı. A seviyesinin belirli koşullara göre belirlenmesi gerektiğine inanıyordu. Örneğin, parçacık fiziğinde bu 0.01'dir.

p- anlamlılık düzeyi
P-değeri terimi ilk kez 1960'ta Brownley'in eserinde kullanılmıştır. P seviyesi (p değeri), sonuçların gerçeğiyle ters orantılı bir göstergedir. En yüksek katsayı p değeri, değişkenler arasındaki bağımlılık örneğinde en düşük güven düzeyine karşılık gelir.
Bu değer, sonuçların yorumuyla ilişkili hata olasılığını yansıtır. Diyelim ki p seviyesi = 0,05 (1/20). Örnekte bulunan değişkenler arasındaki ilişkinin, örneğin rastgele bir özelliği olması olasılığını yüzde beş olarak göstermektedir.Yani, eğer bu bağımlılık yoksa, o zaman tekrarlanan bu denemelerle ortalama olarak, her yirminci çalışmada, değişkenler arasında aynı veya daha fazla bağımlılık beklenebilir. Genellikle, p seviyesi hata seviyesinin “kabul edilebilir marjı” olarak kabul edilir.
Bu arada, p-değeri değişkenler arasındaki gerçek ilişkiyi yansıtmayabilir, ancak varsayımlar içinde sadece belirli bir ortalama değeri gösterir. Özellikle, verilerin nihai analizi, bu katsayının seçilen değerlerine de bağlı olacaktır. P düzeyi = 0,05 olduğunda, bazı sonuçlar ve 0,01 katsayısı olan diğerleri olacaktır.

İstatistiksel hipotezleri test etme
İstatistiksel anlamlılık düzeyi, hipotezleri test ederken özellikle önemlidir. Örneğin, iki taraflı bir test hesaplanırken, reddetme alanı numune dağılımının her iki ucunda (sıfır koordinatına göre) eşit olarak bölünür ve verinin gerçekliği hesaplanır.
Farz edelim ki, belli bir süreci (fenomen) izlerken, yeni istatistiksel bilginin önceki değerlere göre küçük değişiklikler gösterdiği ortaya çıktı. Ayrıca, sonuçlardaki farklılıklar küçük, açık değil, ancak çalışma için önemli. İkilem uzmandan önce ortaya çıkar: değişiklikler gerçekten oluyor mu veya bu örnekleme hataları (yanlış ölçümler)?
Bu durumda, boş hipotez ya kullanılır ya da reddedilir (hepsi bir hataya atfedilir ya da sistemdeki değişiklik bir kesin tamamlanma olarak kabul edilir). Sorunu çözme süreci, toplam istatistiksel anlamlılığın (p-değeri) ve anlamlılık seviyesinin (α) oranına dayanmaktadır. P seviyesi <α ise boş hipotezi reddedilir. P değeri ne kadar küçük olursa, test istatistiği o kadar anlamlı olur.
Kullanılan Değerler
Önem derecesi, analiz edilen materyale bağlıdır. Uygulamada aşağıdaki sabit değerler kullanılır:
- a = 0,1 (veya% 10);
- a = 0.05 (veya% 5);
- a = 0.01 (veya% 1);
- a = 0.001 (veya% 0.1).
Hesaplamalar ne kadar doğru olursa, α katsayısı o kadar düşük olur. Doğal olarak, fizik, kimya, ilaç, genetikle ilgili istatistiksel tahminler siyaset bilimi ve sosyolojiden daha fazla doğruluk gerektirir.

Belirli alanlarda alaka düzeyi eşikleri
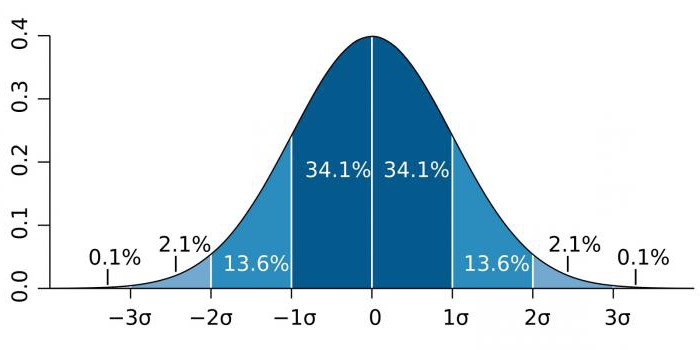
Parçacık fiziği ve üretim faaliyetleri gibi yüksek hassasiyetli alanlarda, istatistiksel önem genellikle, normal olasılık dağılımına (Gauss dağılımı) göre standart sapmanın (sigma katsayısı - σ ile gösterilir) oranı olarak ifade edilir. σ, matematiksel beklentilere göre belirli bir değerin değerlerinin dağılımını belirleyen istatistiksel bir göstergedir. Olayların olasılığını çizmek için kullanılır.
Bilgi alanına bağlı olarak σ katsayısı büyük ölçüde değişir. Örneğin, Higgs bozonunun varlığını tahmin ederken, σ parametresi beş (σ = 5), ki bu p-değeri = 1 / 3.5 milyon değerine tekabül ediyor Genom çalışmalarında, anlamlılık düzeyi 5 x 10 olabilir.-8Bu bölge için nadir değildir.
etki
Α ve p değerlerinin katsayılarının doğru özellikler olmadığını unutmayın. Çalışılan olgunun istatistiklerinde anlamlılık düzeyi ne olursa olsun, hipotezi kabul etmek için koşulsuz bir temel değildir. Örneğin, α'nın değeri ne kadar küçükse, oluşturulan hipotezin anlamlı olma olasılığı o kadar artar. Ancak, çalışmanın istatistiksel gücünü (önemini) azaltan bir hata riski vardır.
Yalnızca istatistiksel olarak anlamlı sonuçlara odaklanan araştırmacılar hatalı sonuçlar alabilir. Aynı zamanda, varsayımlarını kullandıkları için (aslında, α ve p-değeri olan) çalışmalarını iki kez kontrol etmek zordur. Bu nedenle, istatistiki anlamlılığın büyüklüğü - başka bir gösterge belirlemek için her zaman istatistiksel anlamlılığın hesaplanması ile birlikte tavsiye edilir. Bir etkinin büyüklüğü, etkinin gücünün niceliksel bir ölçüsüdür.
