Tahap penting dalam statistik adalah petunjuk penting yang mencerminkan tahap kepercayaan pada ketepatan dan kebenaran data yang diterima (ramalan). Konsep ini digunakan secara meluas dalam pelbagai bidang: dari menjalankan penyelidikan sosiologi, kepada ujian statistik hipotesis saintifik.

Definisi
Tahap kepentingan statistik (atau keputusan penting secara statistik) menunjukkan kebarangkalian kejadian tidak sengaja petunjuk yang dikaji. Kepentingan statistik umum fenomena ini dinyatakan oleh pekali p-nilai (p-level). Dalam mana-mana percubaan atau pemerhatian, kemungkinan data yang diperoleh adalah disebabkan oleh kesilapan pensampelan. Ini benar terutama untuk sosiologi.
Iaitu, statistik secara statistik adalah ketara yang kebarangkalian kejadian tidak sengaja sangat kecil atau cenderung melampau. Melampau dalam konteks ini dianggap tahap penyelewengan statistik dari hipotesis nol (hipotesis yang diperiksa untuk konsisten dengan data sampel yang diperoleh). Dalam amalan saintifik, tahap kepentingan dipilih sebelum pengumpulan data dan, sebagai peraturan, pekali adalah 0.05 (5%). Bagi sistem di mana nilai yang tepat sangat penting, penunjuk ini boleh menjadi 0.01 (1%) atau kurang.
Latar Belakang
Konsep tahap kepentingan telah diperkenalkan oleh ahli statistik dan ahli sejarah British, Ronald Fisher pada tahun 1925 ketika ia mengembangkan metodologi untuk menguji hipotesis statistik. Apabila menganalisis suatu proses, terdapat kebarangkalian fenomena tertentu. Kesukaran timbul apabila bekerja dengan kebarangkalian peratus kecil (atau tidak jelas) yang berada di bawah konsep "ralat pengukuran."
Apabila bekerja dengan statistik yang tidak cukup spesifik untuk disahkan, saintis menghadapi masalah hipotesis nol, yang "mengganggu" dengan kuantiti yang kecil. Fisher menyarankan untuk menentukan sistem tersebut kebarangkalian peristiwa 5% (0.05) sebagai kepingan selektif mudah, yang membolehkan anda menolak hipotesis nol dalam pengiraan.
Pengenalan pekali tetap
Pada tahun 1933, para saintis Jerzy Neumann dan Egon Pearson dalam karya mereka mencadangkan terlebih dahulu (sebelum pengumpulan data) untuk menubuhkan tahap tertentu. Contoh-contoh penggunaan peraturan ini jelas kelihatan semasa pemilihan. Katakan ada dua calon, salah satunya adalah sangat popular, dan yang kedua kurang diketahui. Jelas, calon pertama memenangi pilihan raya, dan peluang kedua cenderung kepada sifar. Mereka berusaha - tetapi tidak sama: selalu ada kebarangkalian force majeure, maklumat sensasi, keputusan tak terduga yang dapat mengubah hasil pemilihan yang diramalkan.
Neumann dan Pearson bersetuju bahawa tahap kepentingan yang dicadangkan oleh Fisher sebanyak 0.05 (dilambangkan oleh simbol α) adalah paling mudah. Walau bagaimanapun, Fisher sendiri pada tahun 1956 menentang penetapan nilai ini. Beliau percaya bahawa tahap α perlu diwujudkan mengikut keadaan tertentu. Sebagai contoh, dalam fizik zarah itu adalah 0.01.

P-value
Istilah nilai p-pertama kali digunakan dalam kerja Brownley pada tahun 1960. P-level (p-value) adalah penunjuk yang berlawanan dengan kebenaran hasilnya. Pekali tertinggi p-nilai sepadan dengan tahap keyakinan yang paling rendah dalam sampel pergantungan antara pembolehubah.
Nilai ini mencerminkan kebarangkalian kesilapan yang berkaitan dengan tafsiran hasilnya. Katakan p-level = 0.05 (1/20). Ia menunjukkan kebarangkalian lima peratus bahawa hubungan antara pembolehubah yang terdapat dalam sampel hanyalah ciri rawak sampel.Iaitu, jika pergantungan ini tidak hadir, maka dengan eksperimen seperti ini, secara purata, dalam setiap dua puluh kajian, seseorang boleh mengharapkan pergantungan yang sama atau lebih besar antara pembolehubah. Selalunya, tahap p dianggap sebagai "margin yang boleh diterima" dari tahap ralat.
Dengan cara ini, p-nilai mungkin tidak mencerminkan hubungan sebenar antara pembolehubah, tetapi hanya menunjukkan nilai purata tertentu dalam andaian. Khususnya, analisis akhir data juga bergantung pada nilai terpilih pekali ini. Dengan p-level = 0.05, akan ada beberapa keputusan, dan dengan pekali 0.01, yang lain.

Menguji hipotesis statistik
Tahap penting statistik amat penting apabila menguji hipotesis. Sebagai contoh, apabila mengira ujian dua sisi, kawasan penolakan dibahagi sama pada kedua-dua hujung pengedaran sampel (berbanding koordinat sifar) dan kebenaran data dikira.
Katakan, apabila memantau proses (fenomena) tertentu, ternyata bahawa maklumat statistik baru menunjukkan perubahan kecil berbanding nilai sebelumnya. Selain itu, percanggahan dalam keputusan adalah kecil, tidak jelas, tetapi penting untuk kajian ini. Dilema timbul sebelum pakar: apakah perubahan benar-benar berlaku atau kesilapan pensampelan ini (ukuran yang tidak tepat)?
Dalam kes ini, hipotesis nol sama ada digunakan atau ditolak (semua disebabkan oleh ralat, atau perubahan dalam sistem diiktiraf sebagai fait accompli). Proses penyelesaian masalah adalah berdasarkan kepada nisbah jumlah nilai statistik (p-nilai) dan tahap signifikans (α). Jika tahap p <α, maka hipotesis nol ditolak. Semakin kecil nilai p, semakin penting ialah statistik ujian.
Nilai yang digunakan
Tahap penting bergantung kepada bahan yang dianalisis. Dalam amalan, nilai tetap berikut digunakan:
- α = 0.1 (atau 10%);
- α = 0.05 (atau 5%);
- α = 0.01 (atau 1%);
- α = 0.001 (atau 0.1%).
Lebih tepat pengiraan diperlukan, semakin rendah pekali α digunakan. Secara semulajadi, ramalan statistik dalam fizik, kimia, farmaseutikal, genetik memerlukan ketepatan yang lebih besar daripada sains politik, sosiologi.

Ambang relevan dalam bidang tertentu
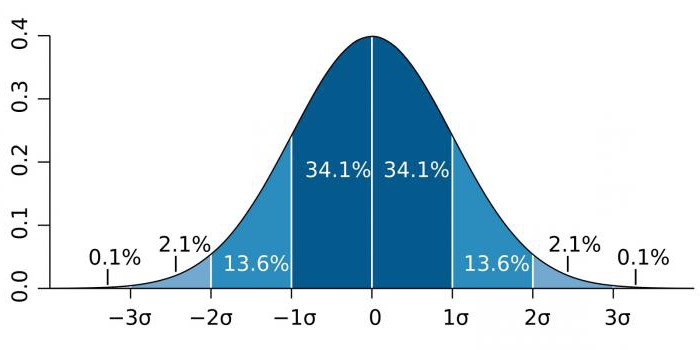
Dalam bidang ketepatan tinggi, seperti fizik zarah dan aktiviti pembuatan, kepentingan statistik sering dinyatakan sebagai nisbah sisihan piawai (dilambangkan oleh pekali sigma - σ) berbanding dengan taburan kebarangkalian normal (pengedaran Gaussian). σ adalah penunjuk statistik yang menentukan penyebaran nilai nilai tertentu berbanding harapan matematik. Digunakan untuk merancang kebarangkalian peristiwa.
Bergantung pada bidang pengetahuan, pekali σ sangat berbeza. Sebagai contoh, apabila meramal kewujudan boson Higgs, parameter σ adalah lima (σ = 5), yang sepadan dengan nilai p-value = 1 / 3.5 juta. Dalam kajian genom, tahap kepentingan boleh 5 × 10-8yang tidak biasa untuk kawasan ini.
Keberkesanan
Perlu diingat bahawa pekali α dan nilai-p tidak merupakan ciri yang tepat. Walau apa pun tahap penting dalam statistik fenomena yang dikaji, ia bukan asas tanpa syarat untuk menerima hipotesis. Sebagai contoh, semakin kecil nilai α, semakin besar kemungkinan bahawa hipotesis yang ditetapkan adalah signifikan. Walau bagaimanapun, terdapat risiko kesilapan, yang mengurangkan kuasa statistik (signifikans) kajian.
Penyelidik yang memberi tumpuan semata-mata kepada keputusan yang signifikan secara statistik boleh membuat kesimpulan yang salah. Pada masa yang sama, sukar untuk menyemak semula kerja mereka, kerana mereka menggunakan asumsi (yang, sebenarnya, adalah nilai-nilai α dan nilai p). Oleh itu, selalu disyorkan, bersama-sama dengan pengiraan kepentingan statistik, untuk menentukan satu lagi petunjuk - magnitud kesan statistik. Besarnya kesan adalah ukuran kuantitatif kekuatan kesan.
