Nozīmīguma līmenis statistikā ir svarīgs rādītājs, kas atspoguļo ticamības pakāpi saņemto (paredzamo) datu precizitātei un patiesībai. Jēdziens tiek plaši izmantots dažādās jomās: no socioloģisko pētījumu veikšanas līdz zinātnisko hipotēžu statistiskai pārbaudei.

Definīcija
Statistiskās nozīmības līmenis (vai statistiski nozīmīgais rezultāts) parāda, kāda ir pētāmo rādītāju nejaušas parādīšanās varbūtība. Fenomena vispārējo statistisko nozīmīgumu izsaka ar koeficientu p-vērtību (p-līmeni). Jebkurā eksperimentā vai novērojumā, visticamāk, iegūtie dati ir saistīti ar izlases kļūdām. Īpaši tas attiecas uz socioloģiju.
Tas ir, statistika ir statistiski nozīmīga, kuras nejaušas parādīšanās varbūtība ir ārkārtīgi maza vai tiecas uz galējībām. Ārkārtējs šajā kontekstā tiek uzskatīts par statistikas novirzes pakāpi no nulles hipotēzes (hipotēzes, kas tiek pārbaudīta, lai tā atbilstu iegūtajiem izlases datiem). Zinātniskajā praksē nozīmīguma līmeni izvēlas pirms datu vākšanas, un parasti tā koeficients ir 0,05 (5%). Sistēmās, kur precīzas vērtības ir ārkārtīgi svarīgas, šis rādītājs var būt 0,01 (1%) vai mazāks.
Pamatinformācija
Svarīguma līmeņa jēdzienu ieviesa britu statistiķis un ģenētiķis Ronalds Fišers 1925. gadā, kad viņš izstrādāja statistisko hipotēžu pārbaudes metodiku. Analizējot procesu, pastāv noteikta parādību varbūtība. Grūtības rodas, strādājot ar nelielām (vai nenozīmīgām) procentu varbūtībām, kuras ietilpst jēdzienā "mērījumu kļūda".
Strādājot ar statistiku, kas nav pietiekami specifiska, lai pārbaudītu, zinātnieki saskārās ar nulles hipotēzes problēmu, kas “traucē” maziem daudzumiem. Fišers ierosināja definēt šādas sistēmas notikumu varbūtība 5% (0,05) kā ērta selektīva šķēle, kas ļauj noraidīt nulles hipotēzi aprēķinos.
Fiksēta koeficienta ieviešana
1933. gadā zinātnieki Jerzy Neumann un Egon Pearson savos darbos jau iepriekš (pirms datu vākšanas) ieteica noteikt noteiktu nozīmīguma līmeni. Šo noteikumu izmantošanas piemēri ir skaidri redzami vēlēšanu laikā. Pieņemsim, ka ir divi kandidāti, no kuriem viens ir ļoti populārs, bet otrais ir maz zināms. Acīmredzot vēlēšanās uzvar pirmais kandidāts, un otrā izredzes mēdz būt nulles. Viņi cenšas, bet nav vienlīdzīgi: vienmēr pastāv nepārvaramas varas varbūtība, sensacionāla informācija, negaidīti lēmumi, kas var mainīt paredzamos vēlēšanu rezultātus.
Neimans un Pīrsons bija vienisprātis, ka Fišera ierosinātais nozīmīguma līmenis 0,05 (apzīmēts ar simbolu α) ir visērtākais. Tomēr pats Fišers 1956. gadā iebilda pret šīs vērtības fiksēšanu. Viņš uzskatīja, ka α līmenis jānosaka saskaņā ar īpašiem apstākļiem. Piemēram, daļiņu fizikā tas ir 0,01.

P-vērtība
Termins p-vērtība pirmo reizi tika izmantots Braunlija darbā 1960. gadā. P līmenis (p vērtība) ir rādītājs, kas ir apgriezti saistīts ar rezultātu patiesumu. Augstākā koeficienta p vērtība atbilst zemākajam ticamības līmenim mainīgo atkarības paraugā.
Šī vērtība atspoguļo kļūdu iespējamību, kas saistīta ar rezultātu interpretāciju. Pieņemsim, ka p līmenis = 0,05 (1/20). Tas parāda piecu procentu varbūtību, ka attiecības starp izlasē atrastajiem mainīgajiem ir tikai izlases nejauša pazīme.Tas ir, ja šīs atkarības nav, tad ar atkārtotiem šādiem eksperimentiem vidēji katrā divdesmitajā pētījumā var gaidīt tādu pašu vai lielāku atkarību starp mainīgajiem. Bieži vien p-līmenis tiek uzskatīts par kļūdas līmeņa “pieņemamo rezervi”.
Starp citu, p-vērtība var neatspoguļot reālās attiecības starp mainīgajiem, bet tikai parāda noteiktu vidējo vērtību pieņēmumos. Jo īpaši datu galīgā analīze būs atkarīga arī no izvēlētajām šī koeficienta vērtībām. Ar p līmeni = 0,05, daži rezultāti būs, bet ar koeficientu 0,01 - citi.

Statistisko hipotēžu pārbaude
Pārbaudot hipotēzes, statistikas nozīmīguma līmenis ir īpaši svarīgs. Piemēram, aprēķinot divpusēju pārbaudi, noraidīšanas laukumu sadala vienādi abos parauga sadalījuma galos (attiecībā pret nulles koordinātu) un aprēķina datu patiesumu.
Pieņemsim, ka, pārraugot noteiktu procesu (parādību), izrādījās, ka jaunā statistiskā informācija norāda uz nelielām izmaiņām attiecībā pret iepriekšējām vērtībām. Turklāt rezultātu neatbilstības ir nelielas, nav acīmredzamas, bet ir svarīgas pētījumam. Speciālistam rodas dilemma: vai tiešām notiek izmaiņas vai arī šīs ir paraugu ņemšanas kļūdas (neprecīzi mērījumi)?
Šajā gadījumā tiek izmantota vai noraidīta nulles hipotēze (to visu attiecina uz kļūdu, vai arī izmaiņas sistēmā tiek atzītas par faktisku izpildījumu). Problēmas risināšanas process balstās uz kopējo statistisko nozīmīgumu (p-vērtību) un nozīmīguma līmeni (α). Ja p līmenis <α, tad nulles hipotēze tiek noraidīta. Jo mazāka p-vērtība, jo nozīmīgāka ir testa statistika.
Izmantotās vērtības
Nozīmīguma līmenis ir atkarīgs no analizējamā materiāla. Praksē tiek izmantotas šādas fiksētās vērtības:
- α = 0,1 (vai 10%);
- α = 0,05 (vai 5%);
- α = 0,01 (vai 1%);
- α = 0,001 (vai 0,1%).
Jo precīzāki ir aprēķini, jo mazāks ir koeficients α. Protams, statistikas prognozes fizikā, ķīmijā, farmācijā un ģenētikā prasa lielāku precizitāti nekā politoloģijā, socioloģijā.

Atbilstības sliekšņi konkrētās jomās
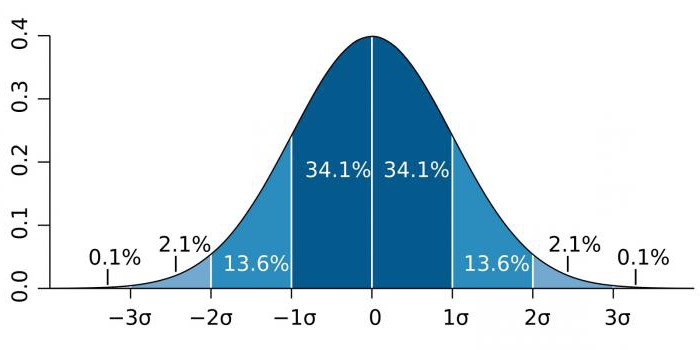
Augstas precizitātes jomās, piemēram, daļiņu fizikā un ražošanas darbībās, statistisko nozīmīgumu bieži izsaka kā standartnovirzes (apzīmētas ar sigma koeficientu - σ) attiecību pret normālo varbūtības sadalījumu (Gausa sadalījumu). σ ir statistiskais rādītājs, kas nosaka noteiktas vērtības vērtību izkliedi attiecībā pret matemātiskajām cerībām. Izmanto notikumu varbūtības attēlošanai.
Koeficients σ ir ļoti atšķirīgs atkarībā no zināšanu jomas. Piemēram, prognozējot Higsa bozona esamību, parametrs σ ir pieci (σ = 5), kas atbilst vērtībai p-vērtība = 1 / 3,5 miljoni. Genomu pētījumos nozīmīguma līmenis var būt 5 × 10-8kas šajā jomā nav nekas neparasts.
Efektivitāte
Paturiet prātā, ka koeficienti α un p vērtība nav precīzi raksturlielumi. Lai kāds būtu nozīmīguma līmenis pētāmās parādības statistikā, tas nav beznosacījuma pamats hipotēzes pieņemšanai. Piemēram, jo mazāka ir α vērtība, jo lielāka ir iespējamība, ka noteiktā hipotēze ir nozīmīga. Tomēr pastāv kļūdas risks, kas samazina pētījuma statistisko jaudu (nozīmīgumu).
Pētnieki, kuri koncentrējas tikai uz statistiski nozīmīgiem rezultātiem, var iegūt kļūdainus secinājumus. Tajā pašā laikā ir grūti vēlreiz pārbaudīt viņu darbu, jo viņi izmanto pieņēmumus (kas patiesībā ir α un p vērtības). Tāpēc vienmēr kopā ar statistiskās nozīmības aprēķināšanu ieteicams noteikt citu rādītāju - statistiskā efekta lielumu. Efekta lielums ir efekta stipruma kvantitatīvs rādītājs.
