Mức ý nghĩa trong thống kê là một chỉ số quan trọng phản ánh mức độ tin cậy về tính chính xác và sự thật của dữ liệu nhận được (dự đoán). Khái niệm này được sử dụng rộng rãi trong các lĩnh vực khác nhau: từ tiến hành nghiên cứu xã hội học, đến kiểm tra thống kê các giả thuyết khoa học.

Định nghĩa
Mức ý nghĩa thống kê (hoặc kết quả có ý nghĩa thống kê) cho thấy xác suất xảy ra ngẫu nhiên của các chỉ số được nghiên cứu là gì. Ý nghĩa thống kê chung của hiện tượng được biểu thị bằng hệ số p-value (mức p). Trong bất kỳ thử nghiệm hoặc quan sát nào, có khả năng dữ liệu thu được là do lỗi lấy mẫu. Điều này đặc biệt đúng với xã hội học.
Đó là, một thống kê có ý nghĩa thống kê mà xác suất xảy ra tình cờ là rất nhỏ hoặc có xu hướng cực đoan. Cực đoan trong bối cảnh này được coi là mức độ sai lệch của thống kê so với giả thuyết null (một giả thuyết được kiểm tra về tính nhất quán với dữ liệu mẫu thu được). Trong thực tiễn khoa học, mức ý nghĩa được chọn trước khi thu thập dữ liệu và theo quy luật, hệ số của nó là 0,05 (5%). Đối với các hệ thống có giá trị chính xác là cực kỳ quan trọng, chỉ báo này có thể là 0,01 (1%) hoặc ít hơn.
Bối cảnh
Khái niệm mức độ quan trọng đã được đưa ra bởi nhà thống kê và nhà di truyền học người Anh Ronald Fisher vào năm 1925 khi ông phát triển một phương pháp để kiểm tra các giả thuyết thống kê. Khi phân tích một quá trình, có một xác suất nhất định của các hiện tượng nhất định. Khó khăn phát sinh khi làm việc với xác suất phần trăm nhỏ (hoặc không rõ ràng) thuộc khái niệm "lỗi đo lường".
Khi làm việc với các số liệu thống kê không đủ cụ thể để xác minh, các nhà khoa học đã phải đối mặt với vấn đề giả thuyết khống, điều này đã can thiệp vào điều tra với số lượng nhỏ. Fisher đề nghị xác định cho các hệ thống như vậy xác suất của sự kiện 5% (0,05) là một lát chọn lọc thuận tiện, cho phép bạn từ chối giả thuyết khống trong các tính toán.
Giới thiệu một hệ số cố định
Năm 1933, các nhà khoa học Jerzy Neumann và Egon Pearson trong các công trình của họ đã đề xuất trước (trước khi thu thập dữ liệu) để thiết lập một mức độ quan trọng nhất định. Ví dụ về việc sử dụng các quy tắc này có thể thấy rõ trong cuộc bầu cử. Giả sử có hai ứng cử viên, một trong số đó là rất phổ biến, và thứ hai là ít được biết đến. Rõ ràng, ứng cử viên đầu tiên giành chiến thắng trong cuộc bầu cử và cơ hội của lần thứ hai có xu hướng bằng không. Họ phấn đấu - nhưng không bằng nhau: luôn có xác suất bất khả kháng, thông tin giật gân, quyết định bất ngờ có thể thay đổi kết quả bầu cử dự đoán.
Neumann và Pearson đồng ý rằng mức ý nghĩa đề xuất của Fisher là 0,05 (ký hiệu là ký hiệu α) là thuận tiện nhất. Tuy nhiên, bản thân Fisher năm 1956 đã phản đối việc ấn định giá trị này. Ông tin rằng mức độ của α nên được thiết lập phù hợp với hoàn cảnh cụ thể. Ví dụ, trong vật lý hạt là 0,01.

Giá trị P
Thuật ngữ p-value lần đầu tiên được sử dụng trong công trình của Brownley vào năm 1960. Cấp độ P (giá trị p) là một chỉ số có liên quan nghịch với sự thật của kết quả. Giá trị p hệ số cao nhất tương ứng với mức độ tin cậy thấp nhất trong mẫu phụ thuộc giữa các biến.
Giá trị này phản ánh xác suất lỗi liên quan đến việc giải thích kết quả. Giả sử mức p = 0,05 (1/20). Nó cho thấy xác suất năm phần trăm rằng mối quan hệ giữa các biến được tìm thấy trong mẫu chỉ là một tính năng ngẫu nhiên của mẫu.Đó là, nếu sự phụ thuộc này không có, thì với các thí nghiệm lặp đi lặp lại như vậy, trung bình, trong mỗi nghiên cứu thứ hai mươi, người ta có thể mong đợi sự phụ thuộc tương tự hoặc lớn hơn giữa các biến. Thông thường, cấp độ p được coi là mức chấp nhận được của mức độ cao của cấp độ lỗi.
Nhân tiện, giá trị p có thể không phản ánh mối quan hệ thực sự giữa các biến, nhưng chỉ hiển thị một giá trị trung bình nhất định trong các giả định. Đặc biệt, phân tích cuối cùng của dữ liệu cũng sẽ phụ thuộc vào các giá trị được chọn của hệ số này. Với mức p = 0,05, sẽ có một số kết quả và với hệ số 0,01, các kết quả khác.

Kiểm định các giả thuyết thống kê
Mức ý nghĩa thống kê đặc biệt quan trọng khi kiểm tra các giả thuyết. Ví dụ: khi tính toán thử nghiệm hai mặt, khu vực loại bỏ được chia đều ở cả hai đầu của phân phối mẫu (liên quan đến tọa độ 0) và tính thật của dữ liệu được tính toán.
Giả sử, khi theo dõi một quá trình (hiện tượng) nhất định, hóa ra thông tin thống kê mới chỉ ra những thay đổi nhỏ so với các giá trị trước đó. Hơn nữa, sự khác biệt trong kết quả là nhỏ, không rõ ràng, nhưng quan trọng đối với nghiên cứu. Vấn đề nan giải nảy sinh trước chuyên gia: những thay đổi có thực sự xảy ra hay là những lỗi lấy mẫu này (các phép đo không chính xác)?
Trong trường hợp này, giả thuyết null được sử dụng hoặc bị từ chối (tất cả được quy cho một lỗi, hoặc sự thay đổi trong hệ thống được công nhận là một lỗi phụ). Quá trình giải quyết vấn đề dựa trên tỷ lệ của tổng ý nghĩa thống kê (giá trị p) và mức ý nghĩa (α). Nếu mức p <α, thì giả thuyết null bị từ chối. Giá trị p càng nhỏ, thống kê kiểm tra càng có ý nghĩa.
Giá trị sử dụng
Mức ý nghĩa phụ thuộc vào vật liệu được phân tích. Trong thực tế, các giá trị cố định sau được sử dụng:
- α = 0,1 (hoặc 10%);
- α = 0,05 (hoặc 5%);
- α = 0,01 (hoặc 1%);
- α = 0,001 (hoặc 0,1%).
Các tính toán được yêu cầu càng chính xác, hệ số α được sử dụng càng thấp. Đương nhiên, dự báo thống kê trong vật lý, hóa học, dược phẩm, di truyền đòi hỏi độ chính xác cao hơn trong khoa học chính trị, xã hội học.

Ngưỡng liên quan trong các lĩnh vực cụ thể
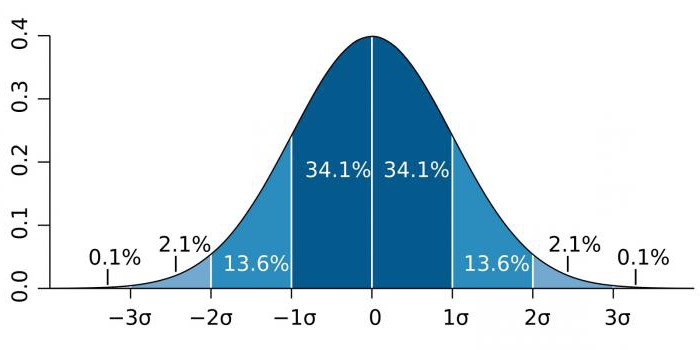
Trong các khu vực có độ chính xác cao, chẳng hạn như vật lý hạt và các hoạt động sản xuất, ý nghĩa thống kê thường được biểu thị bằng tỷ lệ độ lệch chuẩn (biểu thị bằng hệ số sigma -) so với phân phối xác suất thông thường (phân phối Gaussian). là một chỉ số thống kê xác định độ phân tán của các giá trị của một giá trị nhất định so với kỳ vọng toán học. Được sử dụng để vẽ xác suất của các sự kiện.
Tùy thuộc vào lĩnh vực kiến thức, hệ số σ thay đổi rất nhiều. Ví dụ, khi dự đoán sự tồn tại của boson Higgs, tham số σ là năm (= 5), tương ứng với giá trị p-value = 1 / 3,5 triệu. Trong các nghiên cứu về bộ gen, mức ý nghĩa có thể là 5 × 10-8đó không phải là hiếm đối với khu vực này.
Hiệu quả
Hãy nhớ rằng các hệ số α và giá trị p không phải là đặc điểm chính xác. Dù mức độ ý nghĩa trong các thống kê của hiện tượng nghiên cứu, nó không phải là một cơ sở vô điều kiện để chấp nhận giả thuyết. Ví dụ, giá trị của α càng nhỏ thì khả năng giả thuyết được thiết lập càng lớn. Tuy nhiên, có nguy cơ sai sót, làm giảm sức mạnh thống kê (ý nghĩa) của nghiên cứu.
Các nhà nghiên cứu chỉ tập trung vào kết quả có ý nghĩa thống kê có thể nhận được kết luận sai lầm. Đồng thời, rất khó để kiểm tra lại công việc của họ, vì họ sử dụng các giả định (trong thực tế, là giá trị α và p). Do đó, luôn luôn được khuyến nghị, cùng với việc tính toán ý nghĩa thống kê, để xác định một chỉ số khác - độ lớn của hiệu ứng thống kê. Độ lớn của hiệu ứng là thước đo định lượng về độ mạnh của hiệu ứng.
