Ang antas ng kabuluhan sa istatistika ay isang mahalagang tagapagpahiwatig na sumasalamin sa antas ng pagtitiwala sa kawastuhan at katotohanan ng natanggap (hinulaang) data. Ang konsepto ay malawakang ginagamit sa iba't ibang larangan: mula sa pagsasagawa ng pananaliksik sa sosyolohikal, hanggang sa istatistika na pagsusuri ng mga pang-agham na hypotheses.

Kahulugan
Ang antas ng kabuluhan ng istatistika (o makabuluhang resulta ng istatistika) ay nagpapakita kung ano ang posibilidad ng isang hindi sinasadyang nangyari ng mga pinag-aralan na tagapagpahiwatig. Ang pangkalahatang istatistikal na kabuluhan ng hindi pangkaraniwang bagay ay ipinahayag ng koepisyent na p-halaga (p-level). Sa anumang eksperimento o pagmamasid, malamang na ang datos na nakuha ay dahil sa pag-sample ng mga error. Ito ay totoo lalo na para sa sosyolohiya.
Iyon ay, ang isang istatistika ay makabuluhan sa istatistika na ang posibilidad ng hindi sinasadyang nangyari ay napakaliit o may posibilidad na malala. Ang matinding sa kontekstong ito ay itinuturing na antas ng paglihis ng mga istatistika mula sa null hypothesis (isang hypothesis na sinuri para sa pagkakapare-pareho sa nakuha na data ng sample). Sa kasanayang pang-agham, ang antas ng kabuluhan ay pinili bago ang koleksyon ng data at, bilang isang panuntunan, ang koepisyentidad ay 0,05 (5%). Para sa mga sistema kung saan ang mga tumpak na halaga ay napakahalaga, ang tagapagpahiwatig na ito ay maaaring maging 0.01 (1%) o mas kaunti.
Background
Ang konsepto ng antas ng kahalagahan ay ipinakilala ng istatistang Romano at geneticist na si Ronald Fisher noong 1925 nang siya ay bumuo ng isang pamamaraan para sa pagsubok sa mga istatistika na mga hipotesis. Kapag sinusuri ang isang proseso, mayroong isang tiyak na posibilidad ng ilang mga kababalaghan. Ang mga paghihirap ay lumitaw kapag nagtatrabaho sa maliit (o hindi halata) porsyento na mga posibilidad na nahuhulog sa ilalim ng konsepto ng "error sa pagsukat."
Kapag nagtatrabaho sa mga istatistika na hindi sapat na tiyak upang mapatunayan, ang mga siyentipiko ay naharap sa problema ng null hypothesis, na "nakakasagabal" sa maliit na dami. Iminungkahi ni Fisher ang pagtukoy para sa mga naturang sistema posibilidad ng mga kaganapan 5% (0.05) bilang isang maginhawang pili na nagpapahintulot sa iyo na tanggihan ang null hypothesis sa mga kalkulasyon.
Ang pagpapakilala ng isang nakapirming koepisyent
Noong 1933, ang mga siyentipiko na sina Jerzy Neumann at Egon Pearson sa kanilang mga gawa ay inirerekomenda nang maaga (bago ang koleksyon ng data) upang magtatag ng isang tiyak na antas ng kabuluhan. Ang mga halimbawa ng paggamit ng mga patakarang ito ay malinaw na nakikita sa halalan. Ipagpalagay na mayroong dalawang kandidato, ang isa sa mga ito ay napakapopular, at ang pangalawa ay maliit na kilala. Malinaw, ang unang kandidato ay nanalo sa halalan, at ang mga posibilidad ng pangalawa ay may posibilidad na maging zero. Nagsusumikap sila - ngunit hindi pantay: palaging may posibilidad ng lakas ng katahimikan, nakakaalam na impormasyon, hindi inaasahang desisyon na maaaring baguhin ang hinulaang mga resulta ng halalan.
Napagkasunduan nina Neumann at Pearson na ang iminungkahing antas ng kahalagahan ng Fisher na 0.05 (na tinutukoy ng simbolo α) ay pinaka-maginhawa. Gayunpaman, si Fisher mismo sa 1956 ay sumalungat sa pag-aayos ng halagang ito. Naniniwala siya na ang antas ng α ay dapat maitatag alinsunod sa mga tiyak na pangyayari. Halimbawa, sa maliit na pisika na ito ay 0.01.

P-halaga
Ang terminong p-halaga ay unang ginamit sa akda ni Brownley noong 1960. Ang antas ng P (halaga-p) ay isang tagapagpahiwatig na walang kabaligtaran na nauugnay sa katotohanan ng mga resulta. Ang pinakamataas na koepisyent na p-halaga ay tumutugma sa pinakamababang antas ng tiwala sa sample ng pag-asa sa pagitan ng mga variable.
Ang halagang ito ay sumasalamin sa posibilidad ng mga pagkakamali na nauugnay sa pagpapakahulugan ng mga resulta. Ipagpalagay na p-level = 0.05 (1/20). Ipinapakita nito ang limang porsyento na posibilidad na ang ugnayan sa pagitan ng mga variable na natagpuan sa sample ay isang random na tampok lamang ng sample.Iyon ay, kung ang pag-asa na ito ay wala, pagkatapos ay may paulit-ulit na gayong mga eksperimento, sa average, sa bawat ikadalawampu na pag-aaral, maaasahan ng isang tao ang pareho o mas malaking pag-asa sa pagitan ng mga variable. Kadalasan, ang p-level ay itinuturing na "katanggap-tanggap na margin" ng antas ng error.
Sa pamamagitan ng paraan, ang p-halaga ay maaaring hindi sumasalamin sa totoong relasyon sa pagitan ng mga variable, ngunit nagpapakita lamang ng isang tiyak na average na halaga sa loob ng mga pagpapalagay. Sa partikular, ang pangwakas na pagsusuri ng data ay depende din sa mga napiling mga halaga ng koepisyent na ito. Sa isang p-level = 0.05, magkakaroon ng ilang mga resulta, at may isang koepisyent na 0.01, iba pa.

Pagsubok ng mga istatistika na hypotheses
Ang antas ng kabuluhan ng istatistika ay lalong mahalaga kapag sumusubok sa mga hypotheses. Halimbawa, kapag kinakalkula ang isang dalawang panig na pagsubok, ang lugar ng pagtanggi ay nahahati nang pantay sa parehong mga dulo ng pamamahagi ng sample (kamag-anak sa zero coordinate) at ang katotohanan ng data ay kinakalkula.
Ipagpalagay, kapag sinusubaybayan ang isang tiyak na proseso (kababalaghan), lumiliko na ang bagong impormasyon ng istatistika ay nagpapahiwatig ng mga maliit na pagbabago na nauugnay sa mga nakaraang halaga. Bukod dito, ang mga pagkakaiba sa mga resulta ay maliit, hindi halata, ngunit mahalaga para sa pag-aaral. Ang dilema ay lumabas bago ang espesyalista: ang mga pagbabago ba ay nagaganap o ang mga sampling error na ito (hindi tumpak na mga sukat)?
Sa kasong ito, ang null hypothesis ay alinman ay ginamit o tinanggihan (lahat ay iniugnay sa isang error, o ang pagbabago sa system ay kinikilala bilang isang fait accompli). Ang proseso ng paglutas ng problema ay batay sa ratio ng kabuuang istatistikal na kahalagahan (p-halaga) at antas ng kabuluhan (α). Kung ang p-level <α, pagkatapos ay ang null hypothesis ay tinanggihan. Ang mas maliit ang p-halaga, ang mas makabuluhan ay ang istatistika ng pagsubok.
Mga Halagang Ginamit
Ang antas ng kabuluhan ay nakasalalay sa materyal na nasuri. Sa pagsasagawa, ang mga sumusunod na naayos na halaga ay ginagamit:
- α = 0.1 (o 10%);
- α = 0.05 (o 5%);
- α = 0.01 (o 1%);
- α = 0.001 (o 0.1%).
Ang mas tumpak na mga kalkulasyon ay kinakailangan, mas mababa ang koepisyent na α ay ginagamit. Naturally, ang mga istatistikong pagtataya sa pisika, kimika, parmasyutiko, genetika ay nangangailangan ng higit na katumpakan kaysa sa agham pampulitika, sosyolohiya.

Mga kapit na may kaugnayan sa mga tiyak na lugar
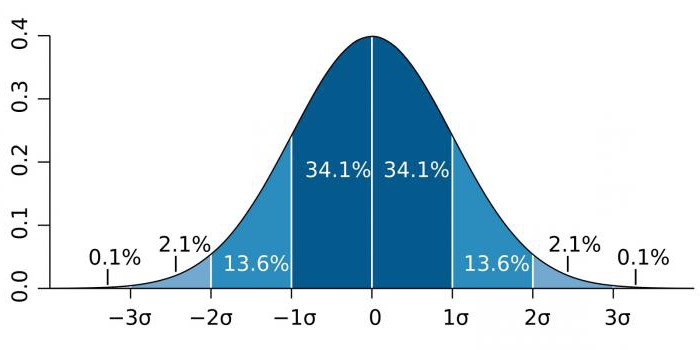
Sa mga lugar na may mataas na katumpakan, tulad ng pisika at aktibidad ng pagmamanupaktura, ang istatistikal na kahalagahan ay madalas na ipinahayag bilang ang ratio ng karaniwang paglihis (na ipinapahiwatig ng koepisyent ng sigma - σ) na nauugnay sa normal na pamamahagi ng posibilidad (pamamahagi ng Gaussian). Ang σ ay isang tagapagpahiwatig ng istatistika na tumutukoy sa pagpapakalat ng mga halaga ng isang tiyak na halaga na nauugnay sa mga inaasahan sa matematika. Ginamit upang balangkas ang posibilidad ng mga kaganapan.
Depende sa larangan ng kaalaman, ang koepisyent σ ay nag-iiba-iba. Halimbawa, kapag hinuhulaan ang pagkakaroon ng Higgs boson, ang parameter σ ay limang (σ = 5), na tumutugma sa halaga ng p-halaga = 1 / 3.5 milyon. Sa mga pag-aaral ng genom, ang antas ng kabuluhan ay maaaring 5 × 10-8hindi bihira ang lugar na ito.
Epektibo
Tandaan na ang mga koepisyenteng α at p-halaga ay hindi tumpak na mga katangian. Anuman ang antas ng kabuluhan sa mga istatistika ng pinag-aralan na hindi pangkaraniwang bagay, hindi ito isang walang pasubali na batayan para sa pagtanggap ng hypothesis. Halimbawa, mas maliit ang halaga ng α, mas malaki ang pagkakataon na ang itinatag na hypothesis ay makabuluhan. Gayunpaman, may panganib ng pagkakamali, na binabawasan ang statistical power (kabuluhan) ng pag-aaral.
Ang mga mananaliksik na nakatuon lamang sa mga makabuluhang resulta ng istatistika ay maaaring makakuha ng mga maling konklusyon. Kasabay nito, mahirap i-double-check ang kanilang trabaho, dahil gumagamit sila ng mga pagpapalagay (na, sa katunayan, ay ang mga halaga ng α at p-halaga). Samakatuwid, palaging inirerekomenda, kasama ang pagkalkula ng kabuluhan ng istatistika, upang matukoy ang isa pang tagapagpahiwatig - ang laki ng statistic na epekto. Ang laki ng isang epekto ay isang dami ng sukat ng lakas ng isang epekto.
