ระดับความสำคัญในสถิติ

ระดับนัยสำคัญในสถิติเป็นตัวบ่งชี้สำคัญที่สะท้อนถึงระดับความเชื่อมั่นในความถูกต้องและความจริงของข้อมูลที่ได้รับ (ทำนาย) แนวคิดนี้ใช้กันอย่างแพร่หลายในด้านต่าง ๆ : จากการดำเนินการวิจัยทางสังคมวิทยาไปจนถึงการทดสอบทางสถิติของสมมติฐานทางวิทยาศาสตร์

คำนิยาม

ระดับนัยสำคัญทางสถิติ (หรือผลลัพธ์ที่มีนัยสำคัญทางสถิติ) แสดงให้เห็นถึงความน่าจะเป็นของการเกิดขึ้นโดยไม่ตั้งใจของตัวชี้วัดที่ศึกษา ความสำคัญทางสถิติทั่วไปของปรากฏการณ์ถูกแสดงออกด้วยค่า p-value (p-level) ในการทดลองหรือการสังเกตใด ๆ มีแนวโน้มว่าข้อมูลที่ได้รับนั้นเกิดจากการสุ่มตัวอย่างข้อผิดพลาด นี่คือความจริงโดยเฉพาะอย่างยิ่งสำหรับสังคมวิทยา

นั่นคือสถิติมีนัยสำคัญทางสถิติที่มีความน่าจะเป็นของการเกิดอุบัติเหตุมีขนาดเล็กมากหรือมีแนวโน้มที่จะสุดขั้ว สุดขีดในบริบทนี้ถือเป็นระดับการเบี่ยงเบนของสถิติจากสมมติฐานว่าง (สมมติฐานที่ตรวจสอบความสอดคล้องกับข้อมูลตัวอย่างที่ได้รับ) ในการปฏิบัติทางวิทยาศาสตร์ระดับความสำคัญจะถูกเลือกก่อนการรวบรวมข้อมูลและตามค่าสัมประสิทธิ์ของมันคือ 0.05 (5%) สำหรับระบบที่ค่าที่ถูกต้องมีความสำคัญอย่างยิ่งตัวบ่งชี้นี้อาจเป็น 0.01 (1%) หรือน้อยกว่า

ประวัติผู้ป่วย

แนวคิดของระดับนัยสำคัญได้รับการแนะนำโดยนักสถิติชาวอังกฤษและนักพันธุศาสตร์โรนัลด์ฟิชเชอร์ในปี 2468 เมื่อเขาพัฒนาวิธีการสำหรับการทดสอบสมมติฐานทางสถิติ เมื่อวิเคราะห์กระบวนการมีความน่าจะเป็นของปรากฏการณ์บางอย่าง ความยากลำบากเกิดขึ้นเมื่อทำงานกับความน่าจะเป็นเปอร์เซ็นต์ (หรือไม่ชัดเจน) ที่ตกอยู่ภายใต้แนวคิดของ "ข้อผิดพลาดการวัด"

เมื่อทำงานกับสถิติที่ไม่เฉพาะเจาะจงเพียงพอที่จะตรวจสอบนักวิทยาศาสตร์ประสบกับปัญหาของสมมติฐานว่างซึ่ง "รบกวน" กับปริมาณน้อย ฟิชเชอร์แนะนำให้กำหนดสำหรับระบบดังกล่าว ความน่าจะเป็นของเหตุการณ์ 5% (0.05) เป็นชิ้นเลือกที่สะดวกช่วยให้คุณปฏิเสธสมมติฐานว่างในการคำนวณ

การแนะนำของสัมประสิทธิ์คงที่

ในปี 1933 นักวิทยาศาสตร์ Jerzy Neumann และ Egon Pearson ในงานของพวกเขาแนะนำล่วงหน้า (ก่อนการรวบรวมข้อมูล) เพื่อสร้างความสำคัญในระดับหนึ่ง ตัวอย่างของการใช้กฎเหล่านี้ชัดเจนในระหว่างการเลือกตั้ง สมมติว่ามีผู้สมัครสองคนคนหนึ่งซึ่งเป็นที่นิยมมากและคนที่สองไม่ค่อยมีใครรู้จัก เห็นได้ชัดว่าผู้สมัครคนแรกชนะการเลือกตั้งและโอกาสที่สองมักจะเป็นศูนย์ พวกเขามุ่งมั่น - แต่ไม่เท่ากัน: มีความน่าจะเป็นของเหตุสุดวิสัยข้อมูลที่น่าตื่นเต้นการตัดสินใจที่ไม่คาดคิดที่สามารถเปลี่ยนแปลงผลการเลือกตั้งที่คาดการณ์ไว้ได้

นอยมันน์และเพียร์สันเห็นด้วยว่าระดับนัยสำคัญของฟิชเชอร์ที่เสนอคือ 0.05 (แทนด้วยสัญลักษณ์α) สะดวกที่สุด อย่างไรก็ตามฟิชเชอร์เองในปี 1956 ไม่เห็นด้วยกับการแก้ไขค่านี้ เขาเชื่อว่าควรกำหนดระดับของαตามสถานการณ์เฉพาะ ตัวอย่างเช่นในฟิสิกส์ของอนุภาคคือ 0.01

ระดับความสำคัญของ p-

ค่า p-value ถูกใช้ครั้งแรกในงานของ Brownley ในปี 1960 P-level (p-value) เป็นตัวบ่งชี้ที่สัมพันธ์กับความจริงของผลลัพธ์ ค่า p-value สัมประสิทธิ์สูงสุดสอดคล้องกับระดับความเชื่อมั่นต่ำสุดในตัวอย่างการพึ่งพาระหว่างตัวแปร

ค่านี้สะท้อนถึงความน่าจะเป็นของข้อผิดพลาดที่เกี่ยวข้องกับการตีความผลลัพธ์ สมมติว่า p-level = 0.05 (1/20) มันแสดงให้เห็นถึงความน่าจะเป็นร้อยละห้าที่ความสัมพันธ์ระหว่างตัวแปรที่พบในกลุ่มตัวอย่างเป็นเพียงคุณลักษณะแบบสุ่มของกลุ่มตัวอย่างนั่นคือถ้าการพึ่งพานี้หายไปจากการทดลองซ้ำแล้วซ้ำอีกโดยเฉลี่ยในการศึกษาที่ยี่สิบทุกคนสามารถคาดหวังว่าการพึ่งพาอาศัยกันระหว่างตัวแปรเดียวกันหรือมากกว่านั้น บ่อยครั้งที่ระดับ p ถือเป็น "ระยะขอบที่ยอมรับได้" ของระดับข้อผิดพลาด

อย่างไรก็ตามค่า p อาจไม่สะท้อนความสัมพันธ์ที่แท้จริงระหว่างตัวแปร แต่แสดงค่าเฉลี่ยที่แน่นอนภายในสมมติฐาน โดยเฉพาะอย่างยิ่งการวิเคราะห์ขั้นสุดท้ายของข้อมูลจะขึ้นอยู่กับค่าที่เลือกของสัมประสิทธิ์นี้ ด้วย p-level = 0.05 จะมีผลลัพธ์บ้างและมีค่าสัมประสิทธิ์เท่ากับ 0.01 และอื่น ๆ

การทดสอบสมมติฐานทางสถิติ

ระดับนัยสำคัญทางสถิติมีความสำคัญอย่างยิ่งเมื่อทำการทดสอบสมมติฐาน ตัวอย่างเช่นเมื่อคำนวณการทดสอบสองด้านพื้นที่การปฏิเสธจะถูกแบ่งเท่า ๆ กันที่ปลายทั้งสองของการแจกตัวอย่าง (เทียบกับศูนย์พิกัด) และการคำนวณความจริงของข้อมูล

สมมติว่าเมื่อตรวจสอบกระบวนการ (ปรากฏการณ์) ปรากฎว่าข้อมูลสถิติใหม่บ่งชี้ว่ามีการเปลี่ยนแปลงเล็กน้อยเมื่อเทียบกับค่าก่อนหน้า ยิ่งไปกว่านั้นความแตกต่างในผลลัพธ์มีขนาดเล็กไม่ชัดเจน แต่มีความสำคัญสำหรับการศึกษา ภาวะที่กลืนไม่เข้าคายไม่ออกเกิดขึ้นก่อนผู้เชี่ยวชาญ: มีการเปลี่ยนแปลงเกิดขึ้นจริงหรือเป็นข้อผิดพลาดการสุ่มตัวอย่างเหล่านี้ (การวัดที่ไม่ถูกต้อง)?

ในกรณีนี้สมมติฐานว่างจะถูกใช้หรือปฏิเสธ (ทั้งหมดเกิดจากข้อผิดพลาดหรือการเปลี่ยนแปลงในระบบได้รับการยอมรับว่าเป็น fait สำเร็จ) กระบวนการในการแก้ปัญหานั้นขึ้นอยู่กับอัตราส่วนของนัยสำคัญทางสถิติทั้งหมด (p-value) และระดับนัยสำคัญ (α) หาก p-level <αดังนั้นสมมติฐานว่างจะถูกปฏิเสธ ยิ่งค่า p-value ยิ่งเล็กลงยิ่งมีนัยสำคัญยิ่งขึ้นคือสถิติการทดสอบ

ค่านิยมใช้

ระดับความสำคัญขึ้นอยู่กับวัสดุที่กำลังวิเคราะห์ ในทางปฏิบัติจะใช้ค่าคงที่ต่อไปนี้:

• α = 0.1 (หรือ 10%);
• α = 0.05 (หรือ 5%);
• α = 0.01 (หรือ 1%);
• α = 0.001 (หรือ 0.1%)

ยิ่งจำเป็นต้องคำนวณให้แม่นยำยิ่งขึ้นใช้ค่าสัมประสิทธิ์αที่ต่ำกว่า การคาดการณ์ทางสถิติในฟิสิกส์เคมีเภสัชศาสตร์พันธุศาสตร์นั้นต้องการความแม่นยำมากกว่าในรัฐศาสตร์สังคมวิทยา

เกณฑ์ของความเกี่ยวข้องในพื้นที่เฉพาะ

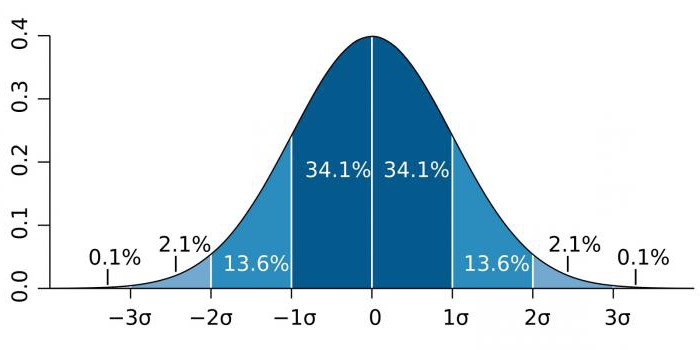
ในพื้นที่ที่มีความแม่นยำสูงเช่นฟิสิกส์ของอนุภาคและกิจกรรมการผลิตนัยสำคัญทางสถิติมักแสดงเป็นอัตราส่วนของค่าเบี่ยงเบนมาตรฐาน (แสดงโดยค่าสัมประสิทธิ์ซิกม่า - σ) ที่สัมพันธ์กับการแจกแจงความน่าจะเป็นปกติ (การแจกแจงแบบเกาส์) σเป็นตัวบ่งชี้ทางสถิติที่กำหนดการกระจายของค่าบางค่าที่สัมพันธ์กับความคาดหวังทางคณิตศาสตร์ ใช้เพื่อวางแผนความน่าจะเป็นของเหตุการณ์

สัมประสิทธิ์σแตกต่างกันอย่างมากขึ้นอยู่กับสาขาความรู้ ตัวอย่างเช่นเมื่อทำนายการมีอยู่ของ Higgs boson พารามิเตอร์σคือห้า (σ = 5) ซึ่งสอดคล้องกับค่า p-value = 1 / 3.5 ล้านในการศึกษาจีโนมระดับนัยสำคัญสามารถ 5 × 10^-8ที่ไม่ใช่เรื่องแปลกสำหรับพื้นที่นี้

ประสิทธิผล

โปรดทราบว่าค่าสัมประสิทธิ์αและ p-value นั้นไม่ถูกต้อง ไม่ว่าระดับนัยสำคัญในสถิติของปรากฏการณ์ที่ศึกษามันไม่ได้เป็นพื้นฐานที่ไม่มีเงื่อนไขสำหรับการยอมรับสมมติฐาน ยกตัวอย่างเช่นยิ่งค่าของαยิ่งน้อยโอกาสที่สมมติฐานที่ตั้งไว้จะมีความสำคัญ อย่างไรก็ตามมีความเสี่ยงที่จะเกิดข้อผิดพลาดซึ่งจะช่วยลดกำลังทางสถิติ (นัยสำคัญ) ของการศึกษา

นักวิจัยที่มุ่งเน้นผลลัพธ์ที่มีนัยสำคัญทางสถิติอาจได้ข้อสรุปที่ผิดพลาด ในเวลาเดียวกันมันเป็นเรื่องยากที่จะตรวจสอบงานของพวกเขาอีกครั้งเนื่องจากพวกเขาใช้สมมติฐาน (ซึ่งอันที่จริงแล้วเป็นค่าของαและ p-value) ดังนั้นจึงขอแนะนำเสมอพร้อมกับการคำนวณนัยสำคัญทางสถิติเพื่อกำหนดตัวบ่งชี้อื่น - ขนาดของผลกระทบทางสถิติ ขนาดของผลคือการวัดเชิงปริมาณของความแข็งแรงของผลกระทบ