"Stohastiskais" ir vārds, ko fiziķi, matemātiķi un citi zinātnieki izmanto, lai aprakstītu procesus, kuriem ir nejaušības elements. Tās izcelsme ir sengrieķu valoda. Tulkojumā tas nozīmē “spēj uzminēt”.
Vārda “stohastiskā” nozīme

"Stohastiskais" ir jēdziens, ko izmanto daudzās dažādās zinātnes jomās. Tas nozīmē kaut ko nejaušību, nejaušību, nenoteiktību. Aristoteļa ētikā (viņa skulpturālais portrets ir parādīts iepriekš) jēdziens “stohastiskais” ir definīcija, kas attiecas uz spēju uzminēt. Acīmredzot matemātiķi to izmantoja, pamatojoties uz to, ka nejaušības elements parādās tieši tad, kad nepieciešams uzminēt. Vārds "stohastisks" ir jēdziens, kas Jaunajā starptautiskajā vārdnīcā definēts kā "minējumi".
Tādējādi var atzīmēt, ka šī jēdziena tehniskā nozīme precīzi neatbilst tā vārdu krājuma (leksiskajai) nozīmei. Daži autori izteicienu "stohastiskais process" izmanto kā sinonīmu terminam "nejaušs process".
Stohastiskums matemātikā

Šī termina izmantošana matemātikā pašlaik ir plaši izplatīta. Piemēram, varbūtību teorijā ir tāds jēdziens kā stohastiskais process. Tās rezultātu nevar noteikt ar šīs sistēmas sākotnējo stāvokli.
Jēdziena "stohastiskums" izmantošana matemātikā tiek attiecināta uz Vladislava Bortskeviča darbiem. Tas bija viņš, kurš lietoja terminu nozīmē "izvirzīt hipotēzes". Matemātikā, it īpaši šādā zinātnes nodaļā kā varbūtības teorija, liela nozīme ir nejaušības principa izpētes laukam. Ir, piemēram, tāda lieta kā stohastiska matrica. Šīs matricas kolonnas vai rindas veido vienu.
Stohastiskā matemātika (finanšu)
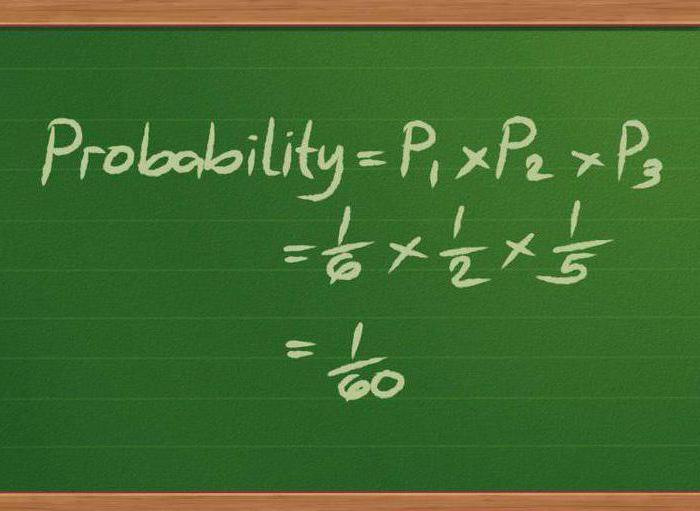
Šajā matemātikas sadaļā tiek analizētas finanšu struktūras, kas darbojas nenoteiktības apstākļos. Tas ir paredzēts, lai atrastu racionālākās finanšu aktīvu un struktūru pārvaldības metodes, ņemot vērā tādus faktorus kā stohastiskā evolūcija, risks, laiks utt.
Zinātnē ir ierasts nošķirt šādas struktūras un objektus, kas tiek izmantoti finanšu matemātikā kopumā:
- firmas (piemēram, uzņēmumi);
- indivīdi;
- starpnieku struktūras (pensiju fondi, bankas);
- finanšu tirgi.
Galvenais stohastiskās finanšu matemātikas izpētes objekts ir tieši pēdējais no tiem. Šī sadaļa ir balstīta uz tādām disciplīnām kā izlases procesu statistika, izlases procesu teorija utt.
Pašlaik pat cilvēkiem, kas ir tālu no zinātnes, no daudziem jaunumiem un publikācijām plašsaziņas līdzekļos ir labi zināms, ka tā dēvēto globālo finanšu indeksu (piemēram, Dow Jones indeksa) vērtības, akciju cenas mainās nejauši. L. Bachelier veica pirmo mēģinājumu, izmantojot matemātiku, aprakstīt akciju cenu attīstību. Viņa stohastiskās metodes pamatā ir varbūtību teorija. L. Bakalaiera disertācija, kurā aprakstīts šis mēģinājums, tika publicēta 1900. gadā. Zinātnieks ir pierādījis formulu, kas šobrīd pazīstama kā patiesās vērtības formula opciju opcijām. Tas atspoguļo stohastisko varbūtību.
Svarīgas idejas, kas vēlāk noveda pie efektīvas tirgus teorijas rašanās, tika izklāstītas M. Kendall darbā, kas publicēts 1953. gadā. Šajā rakstā apskatīts jautājums par akciju cenu dinamiku. Pētnieks to raksturo, izmantojot stohastiskos procesus.
Stohastiskums fizikā
Paldies fiziķiem E. Fermi, S. Ulam, N. Metropolis un D.Neumann tiek plaši izmantota Montekarlo metode. Tās nosaukums cēlies no kazino, kas atrodas tajā pašā pilsētas valstī, piemēram, Monako. Tieši šeit tēvocis Ulams aizņēmās naudu spēlei. Atkārtojuma un iespēju rakstura izmantošana procesu izpētei ir līdzīga tai, kas notiek kazino.

Izmantojot šo modelēšanas metodi, vispirms tiek meklēts varbūtības analogs. Pirms tam modelēšana tika veikta pretējā virzienā: tā tika izmantota, lai pārbaudītu iepriekš iegūtās deterministiskās problēmas rezultātu. Lai arī līdzīgas pieejas pastāvēja pirms Montekarlo metodes atklāšanas, tās nebija populāras un vispārīgas.
Enriko Fermi 1930. gadā izmantoja stohastiskas metodes neitrona īpašību aprēķināšanai, kuras tajā laikā bija tikko atklātas. Montekarlo metodes vēlāk tika izmantotas, strādājot pie Manhetenas projekta, lai gan tajā laikā datoru iespējas bija ievērojami ierobežotas. Šī iemesla dēļ tie kļuva plaši izplatīti tikai pēc datoru parādīšanās.
Stohastiskie signāli
Regulāriem un stohastiskiem signāliem ir dažādas viļņu formas. Ja mēs atkārtoti izmērām pēdējo, mēs iegūstam svārstības, kurām ir jauna forma, kas atšķiras no iepriekšējās, bet parāda būtisku īpašību zināmu līdzību. Stohastiskā signāla piemērs ir jūras viļņu svārstību reģistrēšana.
Kāpēc ir jārunā par šiem diezgan neparastajiem signāliem? Fakts ir tāds, ka automātisko sistēmu izpētē tās ir pat biežāk nekā prognozēts.
Stohastiskums un mākslīgais intelekts
Stohastiskās mākslīgā intelekta programmas darbojas, izmantojot varbūtības metodes. Kā piemēru var minēt tādus algoritmus kā stohastiskā optimizācija vai neironu tīkli. Tas pats attiecas uz modelētiem atkvēlināšanas un ģenētiskajiem algoritmiem. Visos šajos gadījumos stohastiskumu var ietvert problēma pati par sevi vai kaut ko plānot nenoteiktības apstākļos. Modelēšanas aģenta deterministiskā vide ir vienkāršāka nekā stohastiskā.

Tātad, kā mēs redzam, mūs interesējošais jēdziens tiek izmantots daudzās zinātnes jomās. Mēs esam uzskaitījuši un aprakstījuši tikai galvenās tā piemērošanas jomas. Visu šo procesu izpēte, jūs redzat, ir ļoti svarīga un atbilstoša. Tieši tāpēc mūs interesējošais jēdziens, iespējams, ilgu laiku tiks izmantots zinātnē.








