„Stochastinis“ yra žodis, kurį fizikai, matematikai ir kiti mokslininkai vartoja apibūdindami procesus, turinčius atsitiktinumo elementą. Jos kilmė yra senovės graikų kalba. Išvertus tai reiškia „galinti atspėti“.
Žodžio „stochastinis“ reikšmė

„Stochastinis“ yra sąvoka, kuri naudojama daugelyje skirtingų mokslo sričių. Tai reiškia atsitiktinumą, atsitiktinumą, kažko netikrumą. Aristotelio etikoje (jo skulptūrinis portretas pateiktas aukščiau) „stochastinio“ sąvoka yra apibrėžimas, nurodantis gebėjimą atspėti. Akivaizdu, kad matematikai ja pasinaudojo remdamiesi tuo, kad atsitiktinumo elementas atsiranda tik tada, kai reikia atspėti. Žodis „stochastinis“ yra sąvoka, apibrėžta Naujajame tarptautiniame žodyne kaip „spėlionė“.
Taigi galima pastebėti, kad šios sąvokos techninė prasmė tiksliai neatitinka jos leksinės (leksinės) reikšmės. Kai kurie autoriai sąvoką „stochastinis procesas“ naudoja kaip sąvokos „atsitiktinis procesas“ sinonimą.
Stochastiškumas matematikoje

Šiuo metu šis terminas vartojamas matematikoje. Pavyzdžiui, tikimybių teorijoje yra tokia sąvoka kaip stochastinis procesas. Jos rezultato negalima nustatyti pagal pradinę šios sistemos būseną.
„Stochastiškumo“ sąvokos vartojimas matematikoje priskiriamas Vladislavo Bortskevičiaus kūriniams. Būtent jis vartojo terminą reikšdamas „kelti hipotezes“. Matematikoje, ypač tokioje šio mokslo dalyje kaip tikimybių teorija, atsitiktinių tyrimų sritis vaidina svarbų vaidmenį. Pavyzdžiui, yra toks dalykas kaip stochastinė matrica. Šios matricos stulpeliai ar eilutės pridedami prie vieno.
Stochastinė matematika (finansinė)
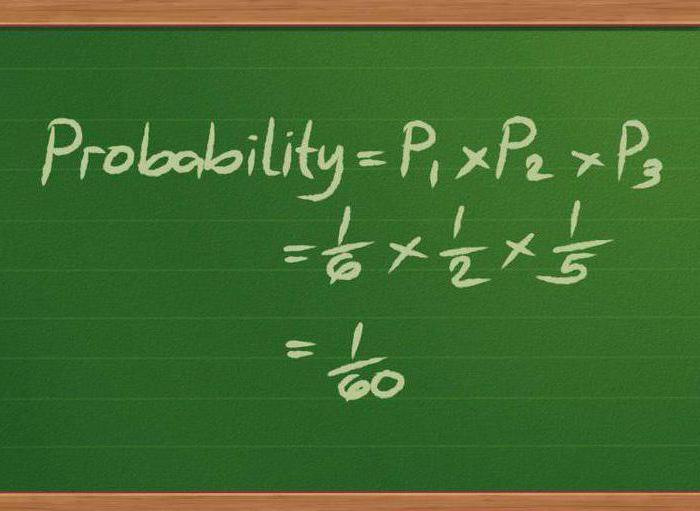
Šiame matematikos skyriuje analizuojamos finansinės struktūros, veikiančios neapibrėžtumo sąlygomis. Jis skirtas rasti racionaliausius finansinio turto ir struktūrų valdymo metodus, atsižvelgiant į tokius veiksnius kaip stochastinė raida, rizika, laikas ir kt.
Moksle įprasta atskirti šias struktūras ir objektus, kurie naudojami visoje finansinėje matematikoje:
- firmos (pavyzdžiui, įmonės);
- asmenys;
- tarpininkų struktūros (pensijų fondai, bankai);
- finansų rinkos.
Pagrindinis stochastinės finansinės matematikos studijų objektas yra būtent paskutinis iš jų. Šis skyrius remiasi tokiomis disciplinomis kaip atsitiktinių procesų statistika, atsitiktinių procesų teorija ir kt.
Šiuo metu net žmonėms, toli nuo mokslo, iš daugybės naujienų ir publikacijų žiniasklaidoje yra gerai žinoma, kad vadinamųjų pasaulinių finansinių indeksų (pvz., Dow Jones indekso) vertės, akcijų kainos keičiasi atsitiktinai. L. Bachelier pirmasis bandė naudodamas matematiką aprašyti akcijų kainų raidą. Jo stochastinis metodas remiasi tikimybių teorija. L. Bachelier disertacija, kurioje pristatomas šis bandymas, buvo paskelbta 1900 m. Mokslininkas įrodė formulę, šiuo metu žinomą kaip tikrosios vertės formulė pirkimo pasirinkimo sandoriams. Tai atspindi stochastinę tikimybę.
Svarbios idėjos, kurios vėliau paskatino veiksmingos rinkos teorijos atsiradimą, buvo pateiktos M. Kendall darbe, paskelbtame 1953 m. Šiame darbe nagrinėjama akcijų kainų dinamikos problema. Tyrėjas aprašo tai taikydamas stochastinius procesus.
Stochastika fizikoje
Ačiū fizikams E. Fermi, S. Ulam, N. Metropolis ir D.Neumannas yra plačiai naudojamas Monte Karlo metodas. Jos pavadinimas kilęs iš kazino, įsikūrusio tame pačiame šalies mieste, tokiame kaip Monakas. Būtent čia dėdė Ulamas pasiskolino pinigų žaidimui. Pasikartojimo ir atsitiktinumų pobūdžio panaudojimas studijų procesams yra panašus į kazino veiklą.

Taikant šį modeliavimo metodą, pirmiausia ieškoma tikimybinio analogo. Prieš tai modeliavimas buvo atliktas priešinga linkme: jis buvo naudojamas anksčiau gautos deterministinės problemos rezultatui patikrinti. Nors panašūs metodai egzistavo dar iki Monte Karlo metodo atradimo, jie nebuvo populiarūs ir bendri.
Enrico Fermi 1930 m. Taikė stochastinius metodus neutrono, kuris tuo metu buvo tik atrastas, savybėms apskaičiuoti. Monte Karlo metodai vėliau buvo naudojami dirbant Manheteno projekte, nors tuo metu kompiuterių galimybės buvo labai ribotos. Dėl šios priežasties jie tapo plačiai paplitę tik pasirodžius kompiuteriams.
Stochastiniai signalai
Reguliarūs ir stochastiniai signalai turi skirtingas bangų formas. Jei pakartotinai išmatuojame pastarąjį, gauname virpesius, kurie turi naują formą, kuri skiriasi nuo ankstesnės, tačiau rodo tam tikrą esminių bruožų panašumą. Stochastinio signalo pavyzdys yra jūros bangos virpesių fiksavimas.
Kodėl reikia kalbėti apie šiuos gana neįprastus signalus? Faktas yra tas, kad tiriant automatines sistemas, jie yra dar labiau paplitę nei prognozuota.
Stochastiškumas ir dirbtinis intelektas
Stochastinės dirbtinio intelekto programos veikia tikimybiniais metodais. Kaip pavyzdį galima paminėti tokius algoritmus kaip stochastinis optimizavimas arba neuroniniai tinklai. Tas pats pasakytina apie imituojamus atkaitinimo ir genetinius algoritmus. Visais šiais atvejais stochastiškumas gali būti įtrauktas į problemą arba planuojant ką nors esant neapibrėžtumui. Deterministinė modeliavimo agento aplinka yra paprastesnė nei stochastinė.

Taigi, kaip matome, susidomėjimo sąvoka vartojama daugelyje mokslo sričių. Mes išvardijome ir apibūdinome tik pagrindines jo taikymo sritis. Visų šių procesų tyrimas, kaip matote, yra labai svarbus ir tinkamas. Štai kodėl dominančios sąvokos moksle greičiausiai bus naudojamos ilgą laiką.








