Korelasyon ve regresyon analizi: örnek, görevler, uygulama. Korelasyon yöntemi ve regresyon analizi

Korelasyon Regresyon Analizi - Bu, sayısal değerler arasındaki ilişkiyi incelemek için en yaygın yöntemlerden biridir. Asıl amacı, iki parametre ile derecesi arasındaki ilişkiyi denklemin daha sonra türetilmesi ile bulmaktır. Örneğin, matematik ve İngilizce sınavını geçen öğrencilerimiz var. Bir testin başarısının başka bir konudaki sonuçları etkileyip etkilemediğini belirlemek için korelasyon kullanabiliriz. Regresyon analizi ile ilgili olarak, İngilizce sınavında puanlanan puanlara dayanarak matematik notlarını tahmin etmeye yardımcı olur ve bunun tersi de geçerlidir.

Korelasyon tablosu nedir?

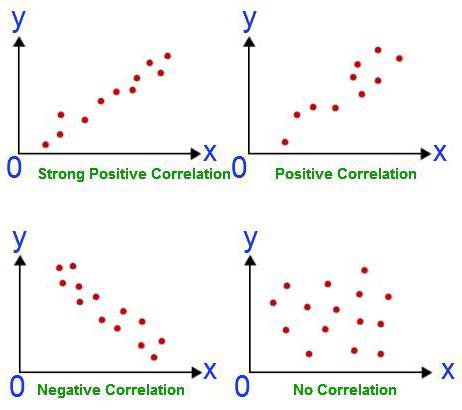
Herhangi bir analiz bilgi toplama ile başlar. Ne kadar fazla olursa, sonuçta elde edilen sonuç o kadar doğru olur. Yukarıdaki örnekte, öğrencilerin bir sınavı geçmeleri gereken iki disipline sahibiz. Başarı oranları bir tahmindir. Korelasyon-regresyon analizi, bir konunun sonucunun ikinci sınavda puanlanan puanları etkileyip etkilemediğini gösterir. Bu soruyu cevaplamak için tüm öğrencilerin derecelendirmelerini paralel olarak analiz etmek gerekir. Ama önce bağımlı değişkene karar vermelisin. Bu durumda, çok önemli değil. Bir matematik sınavının daha önce yapıldığını varsayalım. Üzerindeki noktalar bağımsız bir değişkendir (apsis boyunca ertelenirler). İngilizce daha sonra programa giriyor. Bu nedenle, buna dayanarak yapılan tahminler bağımlı bir değişkendir (koordinat boyunca çizilmiştir). Bu şekilde elde edilen grafik düz bir çizgi gibi göründüğünde, seçilen iki değer arasındaki doğrusal korelasyon daha güçlüdür. Bu, matematikteki öğrencilerin İngilizce sınavında beşinci derece daha iyi olmaları anlamına gelir.

Varsayımlar ve Basitleştirmeler

Korelasyon ve regresyon analizi yöntemi nedensel bir ilişki bulmayı içerir. Bununla birlikte, ilk aşamada, her iki miktardaki değişikliklerin, araştırmacı tarafından henüz dikkate alınmayan üçüncü bir miktardan kaynaklanabileceğini anlamanız gerekir. Değişkenler arasında doğrusal olmayan ilişkiler de olabilir, bu nedenle sıfıra eşit bir katsayı elde etmek deneyin sonu değildir.

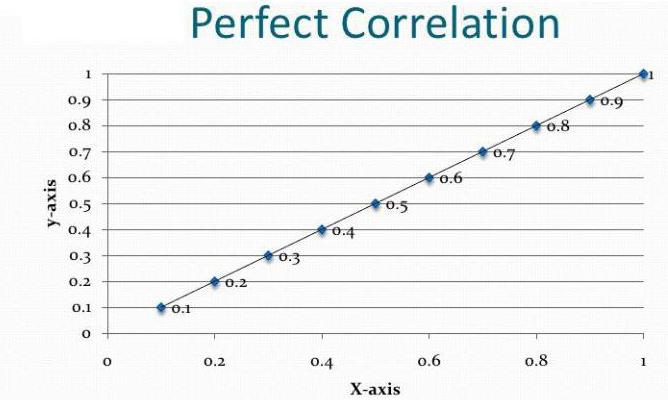
Pearson doğrusal korelasyon

Bu katsayı iki şart altında kullanılabilir. Birincisi - değişkenlerin tüm değerleri rasyonel sayılardır, ikincisi - değerlerin orantılı olarak değişmesi beklenir. Bu katsayı her zaman -1 ile 1 arasındadır. Sıfırdan büyükse, o zaman doğrudan orantılı bir bağımlılık vardır, daha az - ters, eşit - bu değerler birbirini hiçbir şekilde etkilemez. Bu göstergeyi hesaplama yeteneği, korelasyon ve regresyon analizinin temelidir. İlk kez, bu katsayı, Francis Galton fikrine dayanan Karl Pearson tarafından geliştirilmiştir.

Özellikler ve Dikkat Edilecek Noktalar

Pearson korelasyon katsayısı güçlü bir araçtır, ancak dikkatli kullanılmalıdır. Aşağıdaki uyarılar kullanımdadır:

1. Pearson katsayısı, doğrusal bir ilişkinin varlığını veya yokluğunu gösterir. Korelasyon-regresyon analizi burada bitmiyor, değişkenlerin yine de birbirine bağlı olduğu ortaya çıkıyor.
2. Kişi katsayı değerinin yorumlanmasında dikkatli olmalıdır. Bacak büyüklüğü ile IQ seviyesi arasında bir korelasyon bulunabilir.Ancak bu, bir göstergenin diğerini belirlediği anlamına gelmez.
3. Pearson katsayısı göstergeler arasındaki nedensel ilişki hakkında bir şey söylemez.

Spearman's rank korelasyon katsayısı

Bir göstergenin değerindeki bir değişiklik diğerinin değerinde bir artışa veya azalmaya yol açarsa, bu onların ilişkili olduğu anlamına gelir. Bir örneği aşağıda verilecek olan korelasyon-regresyon analizi tam olarak bu parametrelerle bağlantılıdır. Sıra katsayısı, hesaplamaları basitleştirmenize olanak sağlar.

Korelasyon ve regresyon analizi: bir örnek

On işletmenin etkinliğinin bir değerlendirmesi olduğunu varsayalım. Onlara puan veren iki yargıcımız var. Bu durumda işletmenin korelasyon ve regresyon analizi, doğrusal Pearson katsayısı temelinde yapılamaz. Hakimlerin notları arasındaki ilişkiyle ilgilenmiyoruz. İşletmelerin hakimlere göre rütbeleri önemlidir.

Bu tür bir analiz aşağıdaki avantajlara sahiptir:

• İncelenen nicelikleri arasındaki parametrik olmayan ilişki biçimi.
• Kullanım kolaylığı, çünkü rütbeler hem artan değer sırasına hem de azalan düzenine bağlanabilir.

Bu tür bir analizin tek şartı, kaynak verinin dönüştürülmesi ihtiyacıdır.

Uygulama sorunları

Korelasyon ve regresyon analizi, aşağıdaki varsayımlara dayanmaktadır:

• Gözlemler bağımsız olarak kabul edilir (“kartalın” beş katı kaybı, bir sonraki madeni para çevirme sonucunu etkilemez).
• Korelasyon analizinde her iki değişken de rastgele kabul edilir. Regresyonda - sadece bir (bağımlı).
• Bir hipotezi test ederken normal bir dağılıma dikkat edilmelidir. Bağımlı değişkendeki değişiklik, abscissadaki her değer için aynı olmalıdır.
• Korelasyon diyagramı, analizin nihai sonucu değil, sadece iki parametre dizisi arasındaki ilişki hakkındaki hipotezin ilk testidir.

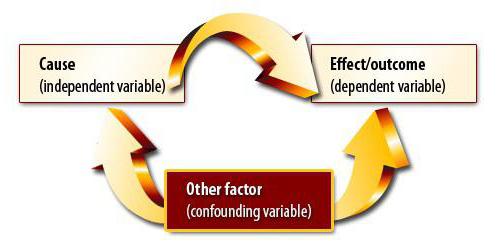
Bağımlılık ve nedensellik

Diyelim ki ihracat hacminin ve GSYH'nin korelasyon katsayısını hesapladık. Birlik modulo eşit olduğu ortaya çıktı. Sonuna kadar korelasyon ve regresyon analizi yaptık mı? Tabii ki hayır. Elde edilen sonuç, GSYİH'nın ihracat yoluyla ifade edilebileceği anlamına gelmez. Göstergeler arasında nedensel bir ilişki olduğunu henüz kanıtlamadık. Korelasyon-regresyon analizi - bir değişkene ait değerleri diğerine göre tahmin etmek. Ancak, çoğu zaman parametreyi etkileyen birçok faktörün olduğunu anlamanız gerekir. İhracat GSYİH'yı belirler, ancak sadece onu değil. Başka faktörler var. Burada, gayri safi yurtiçi hasıladaki diğer bileşenler için düzeltilmiş olmasına rağmen, bir korelasyon ve nedensel bir ilişki vardır.

Başka bir durum çok daha tehlikelidir. İngiltere'de ebeveynleri sigara içen çocukların daha sık suçlu olduğunu gösteren bir anket yapıldı. Bu sonuç, gösterge ile güçlü bir korelasyona dayanmaktadır. Ama o doğru mu? İlk olarak, bağımlılık ters olabilir. Ebeveynler, çocuklarının sürekli değişime uğramaları ve kanunları çiğnemeleri nedeniyle sigaraya başlayabilirler. İkincisi, her iki parametre de üçüncü sebep olabilir. Bu tür aileler, her iki problemle de karakterize edilen düşük sosyal sınıflara aittir. Bu nedenle, korelasyona dayanarak nedensel bir ilişki olduğu sonucuna varılamaz.

Neden regresyon analizi kullanılmalı?

Korelasyon bağımlılığı, miktarlar arasında ilişki bulmayı içerir. Bu davadaki nedensel ilişki perde arkasında kalmaktadır. Korelasyon ve regresyon analizi görevleri sadece iki büyüklüğün değerleri arasındaki ilişkinin varlığını teyit etmek açısından çakışmaktadır. Ancak, başlangıçta araştırmacı nedensel bir ilişki olasılığına dikkat etmez. Regresyon analizi her zaman biri bağımlı olan iki değişkene sahiptir. Birkaç aşamada gerçekleşir:

1. En küçük kareler yöntemini kullanarak doğru modeli seçme.
2. Bağımsız bir değişkende bir değişimin diğerine etkisini açıklayan bir denklemin çıkarılması.

Örneğin, yaşın insan büyümesi üzerindeki etkisini incelersek, regresyon analizi yıllar içindeki değişimleri tahmin etmenize yardımcı olabilir.

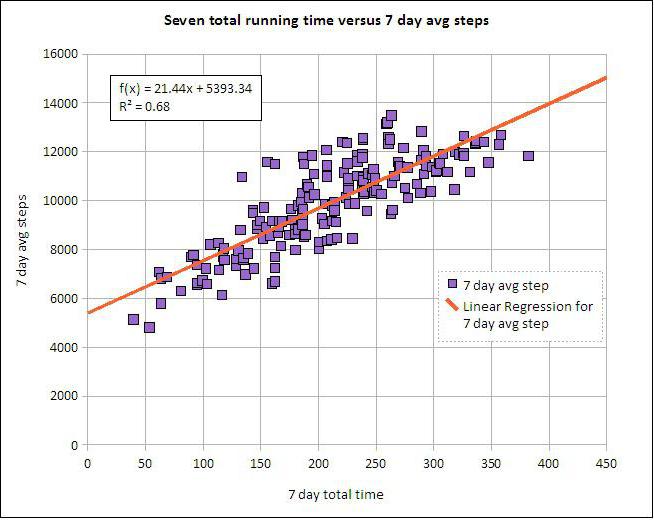
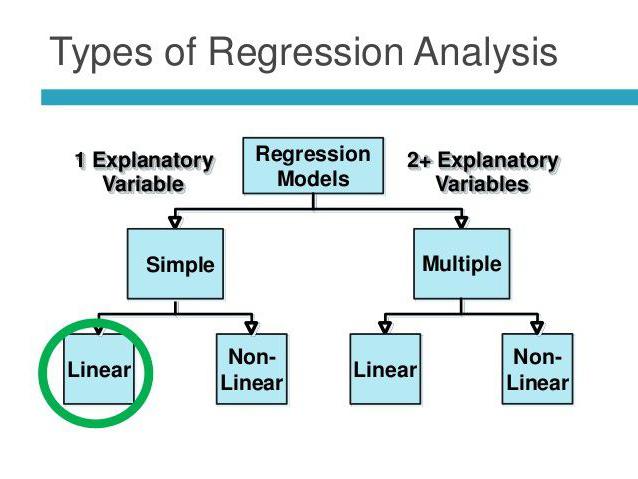
Doğrusal ve çoklu regresyon

X ve Y'nin iki ilişkili değişken olduğunu varsayalım. Regresyon analizi, birisinin diğerinin değerlerine göre büyüklüğünü tahmin etmemize olanak sağlar. Örneğin, olgunluk ve yaş bağımlı belirtilerdir. Aralarındaki ilişki doğrusal regresyon kullanılarak yansıtılır. Aslında, X'i Y ile ya da tam tersi olarak ifade edebilirsiniz. Ancak çoğu zaman regresyon çizgilerinin sadece biri doğrudur. Analizin başarısı büyük ölçüde bağımsız değişkenin doğru belirlenmesine bağlıdır. Örneğin, iki göstergemiz var: verim ve yağış. Günlük deneyimlerden, ilkinin ikinciye bağlı olduğu ve bunun tersi olmadığı açıkça anlaşılmaktadır.

Çoklu regresyon, üç veya daha fazla değişkenin değerlerine dayanarak bilinmeyen bir değer hesaplamanıza izin verir. Örneğin, arazi başına pirinç verimi tane kalitesine, toprak verimliliğine, gübrelere, sıcaklığa ve yağışa bağlıdır. Bu parametrelerin tümü genel sonucu etkiler. Modeli basitleştirmek için aşağıdaki varsayımlar kullanılır:

• Bağımsız ve etkileyici özellikler arasındaki ilişki doğrusaldır.
• Çok hücreli olma hariçtir. Bu, bağımlı değişkenlerin birbirine bağlı olmadığı anlamına gelir.
• Homoskedasticity ve sayı dizilerinin normalliği.

Korelasyon kullanımı ve regresyon analizi

Bu yöntemi kullanmanın üç ana durumu vardır:

1. Miktarlar arasındaki gündelik ilişkilerin test edilmesi. Bu durumda, araştırmacı değişkenin değerlerini belirler ve bağımlı değişkendeki değişikliği etkileyip etkilemediğini bulur. Örneğin, insanlara farklı dozlarda alkol verebilir ve kan basıncını ölçebilirsiniz. Bu durumda araştırmacı, birincinin ikincisinin nedeni olduğundan emin olup, bunun tersi de değildir. Korelasyon-regresyon analizi, bu iki değişken arasında doğrudan orantılı bir doğrusal ilişki saptamanıza ve onu tanımlayan bir formül elde etmenize olanak sağlar. Bu durumda, tamamen farklı ölçüm birimlerinde ifade edilen değerler karşılaştırılabilir.
2. Nedensel bir ilişkiyi genişletmeden iki değişken arasında bir ilişki bulma. Bu durumda, araştırmacının hangi boyutta bağımlı olduğu konusunda bir fark yoktur. Üstelik, gerçekte, her ikisinin de üçüncü değişkenden etkilendiği ve bu nedenle orantılı olarak değiştiği ortaya çıkabilir.
3. Birinden diğerine dayanan değerlerin hesaplanması. Bilinen sayıların ikame edildiği bir denklem üzerine kuruludur.

Dolayısıyla, korelasyon analizi değişkenler arasında bir bağlantı bulmayı (nedensel değil) içerir ve regresyon analizi genellikle matematiksel bir fonksiyon kullanarak açıklar.