"Stochastic" เป็นคำที่นักฟิสิกส์นักคณิตศาสตร์และนักวิทยาศาสตร์คนอื่น ๆ ใช้เพื่ออธิบายกระบวนการที่มีองค์ประกอบของโอกาส ต้นกำเนิดของมันคือกรีกโบราณ แปลแล้วแปลว่า "สามารถเดาได้"
ความหมายของคำว่า "สุ่ม"

"Stochastic" เป็นแนวคิดที่ใช้ในสาขาวิทยาศาสตร์ที่แตกต่างกัน มันหมายถึงความสุ่มความสุ่มความไม่แน่นอนของบางสิ่งบางอย่าง ในจริยธรรมของอริสโตเติล (ภาพประติมากรรมของเขาถูกนำเสนอด้านบน) แนวคิดของ "สุ่ม" เป็นคำจำกัดความที่หมายถึงความสามารถในการเดา เห็นได้ชัดว่านักคณิตศาสตร์ใช้มันบนพื้นฐานที่องค์ประกอบของโอกาสปรากฏขึ้นเมื่อจำเป็นต้องคาดเดา คำว่า "สุ่ม" เป็นแนวคิดที่กำหนดไว้ในพจนานุกรมนานาชาติฉบับใหม่ว่า "การคาดเดา"
ดังนั้นจึงสามารถสังเกตได้ว่าความหมายทางเทคนิคของแนวคิดนี้ไม่ตรงกับความหมายคำศัพท์ (ศัพท์) ของมัน ผู้เขียนบางคนใช้นิพจน์ "กระบวนการสุ่ม" เป็นคำพ้องสำหรับคำว่า "กระบวนการสุ่ม"
สุ่มในคณิตศาสตร์

การใช้คำศัพท์นี้ในวิชาคณิตศาสตร์แพร่หลายขึ้นในปัจจุบัน ตัวอย่างเช่นมีแนวคิดในทฤษฎีความน่าจะเป็นเช่นกระบวนการสุ่ม ไม่สามารถระบุผลลัพธ์ได้โดยสถานะเริ่มต้นของระบบนี้
การใช้งานในคณิตศาสตร์ของแนวคิดของ "ความสุ่ม" นั้นมาจากผลงานของ Vladislav Bortskevich เขาเป็นคนที่ใช้คำในความหมายของ "หยิบยกสมมติฐาน" ในคณิตศาสตร์โดยเฉพาะอย่างยิ่งในส่วนของวิทยาศาสตร์นี้เป็นทฤษฎีความน่าจะเป็นสาขาการวิจัยแบบสุ่มมีบทบาทสำคัญ ยกตัวอย่างเช่นมีตัวอย่างเช่นเมทริกซ์สุ่ม คอลัมน์หรือแถวของเมทริกซ์นี้รวมกันเป็นหนึ่ง
คณิตศาสตร์ Stochastic (การเงิน)
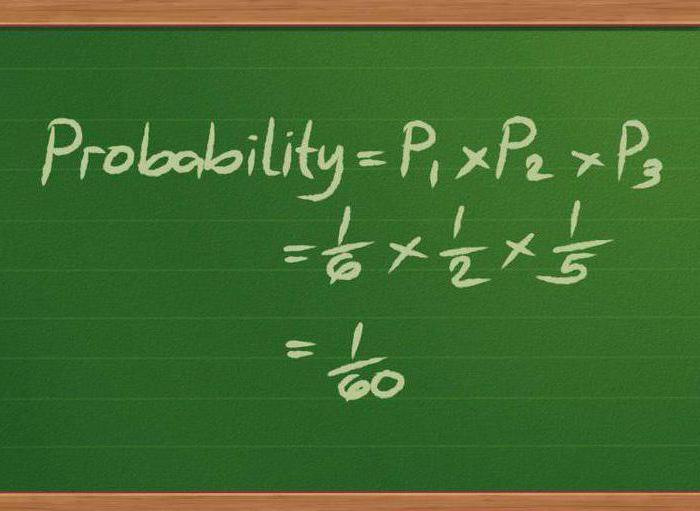
ส่วนนี้ของคณิตศาสตร์วิเคราะห์โครงสร้างทางการเงินที่ดำเนินงานในเงื่อนไขของความไม่แน่นอน มันถูกออกแบบมาเพื่อค้นหาวิธีการที่มีเหตุผลมากที่สุดในการจัดการสินทรัพย์และโครงสร้างทางการเงินโดยคำนึงถึงปัจจัยบัญชีเช่นวิวัฒนาการสุ่มความเสี่ยงเวลา ฯลฯ
ในวิทยาศาสตร์มันเป็นประเพณีที่จะแยกแยะโครงสร้างและวัตถุต่าง ๆ ต่อไปนี้ที่ใช้ในคณิตศาสตร์การเงินโดยรวม:
- บริษัท (ตัวอย่างเช่น บริษัท );
- บุคคล;
- โครงสร้างตัวกลาง (กองทุนบำเหน็จบำนาญ, ธนาคาร);
- ตลาดการเงิน
จุดประสงค์หลักของการศึกษาคณิตศาสตร์ทางการเงินเชิงสุ่มคือจุดสุดท้ายของคณิตศาสตร์ ส่วนนี้จะขึ้นอยู่กับสาขาวิชาเช่นสถิติของกระบวนการสุ่มทฤษฎีของกระบวนการสุ่ม ฯลฯ
ในปัจจุบันแม้กระทั่งคนที่อยู่ห่างไกลจากวิทยาศาสตร์ก็เป็นที่รู้จักกันดีจากข่าวและสิ่งพิมพ์จำนวนมากในสื่อว่าค่าของดัชนีทางการเงินทั่วโลก (ตัวอย่างเช่นดัชนี Dow Jones) ราคาหุ้นเปลี่ยนแปลงแบบสุ่ม L. Bachelier พยายามครั้งแรกเพื่ออธิบายโดยใช้คณิตศาสตร์วิวัฒนาการของราคาหุ้น วิธีสุ่มของเขาขึ้นอยู่กับทฤษฎีความน่าจะเป็น วิทยานิพนธ์ของ L. Bachelier ซึ่งนำเสนอความพยายามนี้ถูกตีพิมพ์ในปี 1900 นักวิทยาศาสตร์ได้พิสูจน์สูตรปัจจุบันที่เรียกว่าสูตรมูลค่ายุติธรรมสำหรับตัวเลือกการโทร มันสะท้อนความน่าจะเป็นแบบสุ่ม
แนวคิดที่สำคัญที่นำไปสู่การเกิดขึ้นของทฤษฎีการตลาดที่มีประสิทธิภาพถูกนำเสนอในงานของ M. Kendall ตีพิมพ์ในปี 1953 บทความนี้กล่าวถึงการเปลี่ยนแปลงของราคาหุ้น ผู้วิจัยอธิบายโดยใช้กระบวนการสโทแคสติก
Stochasticity ในสาขาฟิสิกส์
ขอบคุณนักฟิสิกส์ E. Fermi, S. Ulam, N. Metropolis และ D.นอยมันน์ถูกใช้อย่างกว้างขวางวิธีการมอนติคาร์โล ชื่อของมันมาจากคาสิโนที่ตั้งอยู่ในเมืองเดียวกันในประเทศเช่นโมนาโก มันอยู่ที่นี่ที่ลุง Ulam ยืมเงินสำหรับเกม การใช้ลักษณะของการทำซ้ำและโอกาสในการศึกษากระบวนการคล้ายกับสิ่งที่เกิดขึ้นในคาสิโน

เมื่อใช้วิธีการสร้างแบบจำลองนี้ระบบจะค้นหาอะนาล็อกความน่าจะเป็นครั้งแรก ก่อนหน้านี้การสร้างแบบจำลองได้ดำเนินการในทิศทางตรงกันข้าม: มันถูกใช้เพื่อตรวจสอบผลของปัญหาที่กำหนดขึ้นก่อนหน้านี้ แม้ว่าจะมีวิธีการคล้ายกันก่อนการค้นพบวิธีมอนติคาร์โล แต่ก็ไม่ได้รับความนิยมและทั่วไป
Enrico Fermi ในปี 1930 ได้ใช้เทคนิคสโทแคสติกในการคำนวณคุณสมบัติของนิวตรอนซึ่งเพิ่งถูกค้นพบในเวลานั้น วิธีการ Monte Carlo ถูกนำมาใช้ในภายหลังเมื่อทำงานในโครงการแมนฮัตตันแม้ว่าในเวลานั้นความสามารถของคอมพิวเตอร์มี จำกัด อย่างมีนัยสำคัญ ด้วยเหตุนี้จึงแพร่หลายขึ้นหลังจากคอมพิวเตอร์ปรากฏ
สุ่มสัญญาณ
สัญญาณปกติและสุ่มมีสัญญาณรูปแบบต่างกัน หากเราวัดหลังใหม่เราจะได้รับการแกว่งซึ่งมีรูปร่างใหม่ที่แตกต่างจากก่อนหน้านี้ แต่แสดงความคล้ายคลึงกันบางอย่างในคุณสมบัติที่สำคัญ ตัวอย่างของสัญญาณสุ่มคือการบันทึกการแกว่งของคลื่นทะเล
ทำไมจึงจำเป็นต้องพูดถึงสัญญาณที่ค่อนข้างแปลกประหลาดเหล่านี้? ความจริงก็คือในการศึกษาระบบอัตโนมัติพวกเขาเป็นเรื่องธรรมดามากกว่าที่คาดการณ์ไว้
สุ่มและปัญญาประดิษฐ์
โปรแกรมปัญญาประดิษฐ์ Stochastic ทำงานโดยใช้วิธีความน่าจะเป็น อัลกอริทึมเช่นการเพิ่มประสิทธิภาพสุ่มหรือเครือข่ายประสาทเทียมสามารถอ้างถึงเป็นตัวอย่าง เช่นเดียวกับขั้นตอนวิธีการอบจำลองและพันธุกรรม ในทุกกรณีเหล่านี้ความไม่แน่นอนอาจอยู่ในปัญหาเช่นนี้หรือในการวางแผนบางสิ่งภายใต้สภาพความไม่แน่นอน สภาพแวดล้อมที่กำหนดขึ้นสำหรับเอเจนต์การสร้างแบบจำลองนั้นง่ายกว่าสุ่ม

ดังนั้นตามที่เราเห็นแนวคิดที่น่าสนใจสำหรับเราถูกนำไปใช้ในหลายสาขาวิทยาศาสตร์ เราได้แสดงและกำหนดลักษณะเฉพาะของการใช้งานหลัก การศึกษากระบวนการทั้งหมดนี้เป็นสิ่งสำคัญและมีความเกี่ยวข้อง นั่นคือเหตุผลที่แนวคิดที่น่าสนใจสำหรับเรามีแนวโน้มที่จะถูกนำมาใช้เป็นเวลานานในวิทยาศาสตร์








