การวิเคราะห์ความสัมพันธ์และการถดถอย: ตัวอย่างงานแอปพลิเคชัน วิธีการวิเคราะห์สหสัมพันธ์และการถดถอย

การวิเคราะห์การถดถอยสหสัมพันธ์ - นี่เป็นหนึ่งในวิธีการทั่วไปในการศึกษาความสัมพันธ์ระหว่างค่าตัวเลข เป้าหมายหลักของมันคือการหาความสัมพันธ์ระหว่างพารามิเตอร์ทั้งสองกับระดับของมันพร้อมกับการหาสมการที่ตามมา ตัวอย่างเช่นเรามีนักเรียนที่ผ่านการสอบคณิตศาสตร์และภาษาอังกฤษ เราสามารถใช้สหสัมพันธ์เพื่อกำหนดว่าความสำเร็จของการทดสอบหนึ่งครั้งมีผลต่อผลลัพธ์ในวิชาอื่นหรือไม่ เกี่ยวกับการวิเคราะห์การถดถอยมันช่วยในการทำนายเกรดคณิตศาสตร์ตามคะแนนที่ได้จากการสอบภาษาอังกฤษและในทางกลับกัน

แผนภูมิสหสัมพันธ์คืออะไร

การวิเคราะห์ใด ๆ ที่เริ่มต้นด้วยการรวบรวมข้อมูล ยิ่งได้ผลลัพธ์ที่แม่นยำยิ่งขึ้นในที่สุด ในตัวอย่างข้างต้นเรามีสองสาขาวิชาที่นักเรียนต้องผ่านการสอบ อัตราความสำเร็จของพวกเขาคือการประมาณ การวิเคราะห์ความสัมพันธ์ - ถดถอยแสดงว่าผลของวิชาหนึ่งมีผลต่อคะแนนที่ได้จากการสอบครั้งที่สองหรือไม่ เพื่อที่จะตอบคำถามนี้มันเป็นสิ่งจำเป็นในการวิเคราะห์การให้คะแนนของนักเรียนทุกคนในแบบคู่ขนาน แต่ก่อนอื่นคุณต้องตัดสินใจเลือกตัวแปรตาม ในกรณีนี้มันไม่สำคัญ สมมติว่าการสอบวิชาคณิตศาสตร์เกิดขึ้นก่อนหน้านี้ คะแนนมันเป็นตัวแปรอิสระ (พวกเขาถูกเลื่อนออกไปตาม abscissa) ภาษาอังกฤษเป็นไปตามกำหนดการในภายหลัง ดังนั้นการประมาณการตามมันจึงเป็นตัวแปรตาม ยิ่งกราฟมีลักษณะเป็นเส้นตรงมากเท่าใดยิ่งมีความสัมพันธ์เชิงเส้นตรงมากขึ้นระหว่างค่าที่เลือกทั้งสอง ซึ่งหมายความว่านักเรียนในวิชาคณิตศาสตร์มีแนวโน้มที่จะได้รับห้าในการสอบภาษาอังกฤษ

สมมติฐานและการทำให้เข้าใจง่าย

วิธีการสหสัมพันธ์และการวิเคราะห์การถดถอยเกี่ยวข้องกับการค้นหาความสัมพันธ์เชิงสาเหตุ อย่างไรก็ตามในระยะแรกคุณต้องเข้าใจว่าการเปลี่ยนแปลงในปริมาณทั้งสองอาจเกิดจากบางส่วนที่สามซึ่งนักวิจัยยังไม่ได้คำนึงถึง อาจมีความสัมพันธ์แบบไม่เป็นเส้นตรงระหว่างตัวแปรดังนั้นการได้ค่าสัมประสิทธิ์เท่ากับศูนย์ไม่ได้เป็นจุดสิ้นสุดของการทดสอบ

ความสัมพันธ์เชิงเส้นเพียร์สัน

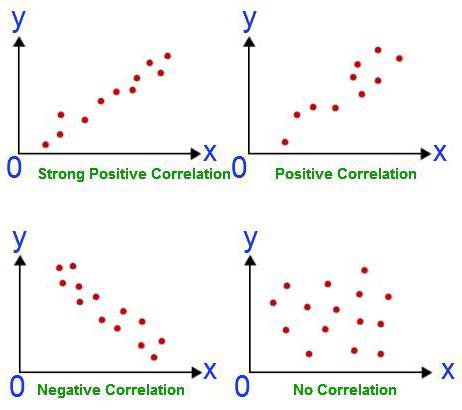
สัมประสิทธิ์นี้สามารถใช้ได้ภายใต้เงื่อนไขสองประการ แรก - ค่าทั้งหมดของตัวแปรเป็นจำนวนตรรกยะที่สอง - คาดว่าค่าจะเปลี่ยนตามสัดส่วน สัมประสิทธิ์นี้อยู่ระหว่าง -1 ถึง 1 เสมอหากมากกว่าศูนย์แสดงว่ามีการพึ่งพาสัดส่วนโดยตรงน้อยกว่า - ผกผันกันเท่ากันค่าเหล่านี้จะไม่ส่งผลกระทบต่อกัน ความสามารถในการคำนวณตัวบ่งชี้นี้เป็นพื้นฐานของการวิเคราะห์สหสัมพันธ์และการถดถอย เป็นครั้งแรกที่ค่าสัมประสิทธิ์นี้พัฒนาโดย Karl Pearson ตามแนวคิดของ Francis Galton

คุณสมบัติและข้อควรระวัง

สัมประสิทธิ์สหสัมพันธ์ของเพียร์สันเป็นเครื่องมือที่ทรงพลัง แต่ก็ควรใช้ด้วยความระมัดระวัง คำเตือนต่อไปนี้ใช้งานอยู่:

1. สัมประสิทธิ์เพียร์สันแสดงว่ามีหรือไม่มีความสัมพันธ์เชิงเส้น การวิเคราะห์ความสัมพันธ์ - การถดถอยไม่ได้จบแค่นั้นมันอาจกลายเป็นว่าตัวแปรนั้นเชื่อมโยงกันอย่างไรก็ตาม
2. จะต้องระมัดระวังในการตีความค่าสัมประสิทธิ์ ความสัมพันธ์สามารถพบได้ระหว่างขนาดขาและระดับ IQแต่นี่ไม่ได้หมายความว่าตัวบ่งชี้ตัวหนึ่งเป็นตัวกำหนดตัวอื่น
3. สัมประสิทธิ์เพียร์สันไม่ได้พูดอะไรเกี่ยวกับความสัมพันธ์เชิงสาเหตุระหว่างตัวบ่งชี้

สัมประสิทธิ์สหสัมพันธ์ของสเปียร์แมน

หากการเปลี่ยนแปลงค่าของตัวบ่งชี้หนึ่งนำไปสู่การเพิ่มหรือลดค่าของตัวบ่งชี้อื่นนั่นหมายความว่าพวกมันเกี่ยวข้องกัน การวิเคราะห์ความสัมพันธ์ - ถดถอยซึ่งเป็นตัวอย่างที่จะได้รับด้านล่างเชื่อมต่อกับพารามิเตอร์ดังกล่าวอย่างแม่นยำ ค่าสัมประสิทธิ์อันดับช่วยให้คุณทำการคำนวณได้ง่ายขึ้น

การวิเคราะห์ความสัมพันธ์และการถดถอย: ตัวอย่าง

สมมติว่ามีการประเมินผลการปฏิบัติงานขององค์กรสิบแห่ง เรามีผู้พิพากษาสองคนที่ให้คะแนนกับพวกเขา การวิเคราะห์สหสัมพันธ์และการถดถอยขององค์กรในกรณีนี้ไม่สามารถทำได้บนพื้นฐานของสัมประสิทธิ์เชิงเส้นเพียร์สัน เราไม่สนใจความสัมพันธ์ระหว่างการจัดอันดับของผู้พิพากษา การจัดอันดับองค์กรตามผู้พิพากษามีความสำคัญ

การวิเคราะห์ประเภทนี้มีข้อดีดังต่อไปนี้:

• รูปแบบความสัมพันธ์แบบไม่มีพารามิเตอร์ระหว่างปริมาณที่ศึกษา
• ความง่ายในการใช้งานเนื่องจากอันดับสามารถนำมาประกอบได้ทั้งในลำดับของมูลค่าและจากมากไปหาน้อย

ความต้องการเพียงอย่างเดียวของการวิเคราะห์ประเภทนี้คือต้องแปลงข้อมูลต้นฉบับ

ปัญหาการใช้งาน

การวิเคราะห์ความสัมพันธ์และการถดถอยจะขึ้นอยู่กับสมมติฐานดังต่อไปนี้:

• การสังเกตถือว่าเป็นอิสระ (สูญเสียห้าเท่าของ "อินทรี" ไม่ส่งผลต่อผลของการโยนเหรียญครั้งต่อไป)
• ในการวิเคราะห์สหสัมพันธ์ตัวแปรทั้งสองนั้นถือเป็นการสุ่ม ในการถดถอย - เพียงหนึ่ง (ขึ้นอยู่กับ)
• เมื่อทดสอบสมมติฐานต้องมีการแจกแจงแบบปกติ การเปลี่ยนแปลงในตัวแปรตามควรจะเหมือนกันสำหรับแต่ละค่าใน abscissa
• แผนภาพความสัมพันธ์เป็นเพียงการทดสอบครั้งแรกของสมมติฐานเกี่ยวกับความสัมพันธ์ระหว่างพารามิเตอร์สองชุดและไม่ใช่ผลสุดท้ายของการวิเคราะห์

การพึ่งพาและสาเหตุ

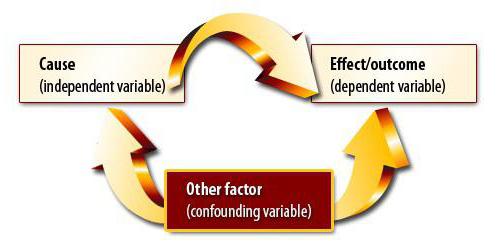
สมมติว่าเราได้คำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของปริมาณการส่งออกและจีดีพี มันกลับกลายเป็นเท่ากับโมดูโลแบบเอกภาพ เราได้ทำการวิเคราะห์สหสัมพันธ์และการถดถอยแล้วหรือยัง? ไม่แน่นอน ผลลัพธ์ที่ได้ไม่ได้หมายความว่าจีดีพีสามารถแสดงผ่านการส่งออกได้ เรายังไม่ได้พิสูจน์ความสัมพันธ์เชิงสาเหตุระหว่างตัวชี้วัด การวิเคราะห์ความสัมพันธ์ - การถดถอย - การคาดการณ์ค่าของตัวแปรหนึ่งตัวตามอีกตัวแปรหนึ่ง อย่างไรก็ตามคุณต้องเข้าใจว่าบ่อยครั้งที่ปัจจัยจำนวนมากมีผลต่อพารามิเตอร์ การส่งออกเป็นตัวกำหนดจีดีพี แต่ไม่เพียงเท่านั้น มีปัจจัยอื่น ๆ ที่นี่มีความสัมพันธ์และความสัมพันธ์เชิงสาเหตุแม้ว่าจะปรับสำหรับส่วนประกอบอื่น ๆ ของผลิตภัณฑ์มวลรวมภายในประเทศ

สถานการณ์อื่นเป็นอันตรายมากขึ้น ในสหราชอาณาจักรมีการสำรวจพบว่าเด็กที่พ่อแม่สูบบุหรี่เป็นผู้กระทำความผิด ข้อสรุปนี้ขึ้นอยู่กับความสัมพันธ์ที่แข็งแกร่งระหว่างตัวบ่งชี้ แต่เขาถูกต้องหรือไม่ ประการแรกการพึ่งพาอาศัยกันอาจเป็นสิ่งที่ตรงกันข้าม ผู้ปกครองสามารถเริ่มสูบบุหรี่เนื่องจากความเครียดจากข้อเท็จจริงที่ว่าลูก ๆ ของพวกเขาได้รับการเปลี่ยนแปลงอย่างต่อเนื่องและผิดกฎหมาย ประการที่สองพารามิเตอร์ทั้งสองอาจเกิดจากการที่สาม ครอบครัวดังกล่าวอยู่ในกลุ่มชนชั้นทางสังคมต่ำซึ่งมีปัญหาทั้งสองประการ ดังนั้นจากความสัมพันธ์จึงไม่สามารถสรุปได้ว่ามีความสัมพันธ์เชิงสาเหตุ

ทำไมต้องใช้การวิเคราะห์การถดถอย

การพึ่งพาความสัมพันธ์เกี่ยวข้องกับการค้นหาความสัมพันธ์ระหว่างปริมาณ ความสัมพันธ์เชิงสาเหตุในกรณีนี้ยังคงอยู่เบื้องหลัง งานของความสัมพันธ์และการวิเคราะห์การถดถอยเกิดขึ้นเฉพาะในแง่ของการยืนยันการดำรงอยู่ของความสัมพันธ์ระหว่างค่าของสองปริมาณ อย่างไรก็ตามในขั้นต้นนักวิจัยไม่สนใจความเป็นไปได้ของความสัมพันธ์เชิงสาเหตุ การวิเคราะห์การถดถอยมีตัวแปรสองตัวเสมอหนึ่งในนั้นขึ้นอยู่กับ มันเกิดขึ้นในหลายขั้นตอน:

1. การเลือกแบบจำลองที่เหมาะสมโดยใช้วิธีกำลังสองน้อยที่สุด
2. การได้มาของสมการที่อธิบายถึงผลกระทบของการเปลี่ยนแปลงในตัวแปรอิสระต่ออีกตัวแปรหนึ่ง

ตัวอย่างเช่นหากเราศึกษาผลกระทบของอายุที่มีต่อการเติบโตของมนุษย์การวิเคราะห์การถดถอยสามารถช่วยทำนายการเปลี่ยนแปลงในช่วงหลายปีที่ผ่านมา

การถดถอยเชิงเส้นและหลาย

สมมติว่า X และ Y เป็นสองตัวแปรที่เกี่ยวข้อง การวิเคราะห์การถดถอยช่วยให้เราสามารถทำนายขนาดของหนึ่งในนั้นขึ้นอยู่กับค่าของอื่น ๆ ตัวอย่างเช่นวุฒิภาวะและอายุขึ้นอยู่กับอาการ ความสัมพันธ์ระหว่างพวกเขาสะท้อนโดยใช้การถดถอยเชิงเส้น ในความเป็นจริงคุณสามารถแสดง X ผ่าน Y หรือในทางกลับกัน แต่บ่อยครั้งเพียงหนึ่งบรรทัดการถดถอยที่ถูกต้อง ความสำเร็จของการวิเคราะห์ส่วนใหญ่ขึ้นอยู่กับการตัดสินใจที่ถูกต้องของตัวแปรอิสระ ตัวอย่างเช่นเรามีสองตัวบ่งชี้: ผลผลิตและการเร่งรัด จากประสบการณ์ในชีวิตประจำวันมันชัดเจนว่าคนแรกขึ้นอยู่กับคนที่สองไม่ใช่ในทางกลับกัน

การถดถอยหลายครั้งทำให้คุณสามารถคำนวณค่าที่ไม่รู้จักตามค่าของตัวแปรตั้งแต่สามตัวแปรขึ้นไป ตัวอย่างเช่นผลผลิตข้าวต่อเอเคอร์ขึ้นอยู่กับคุณภาพของเมล็ดความอุดมสมบูรณ์ของดินปุ๋ยอุณหภูมิและปริมาณน้ำฝน พารามิเตอร์เหล่านี้ทั้งหมดมีผลต่อผลลัพธ์โดยรวม เพื่อทำให้โมเดลง่ายขึ้นมีการใช้สมมติฐานต่อไปนี้:

• ความสัมพันธ์ระหว่างลักษณะอิสระและอิทธิพลที่มีอิทธิพลนั้นเป็นเส้นตรง
• Multicollinearity ไม่รวมอยู่ ซึ่งหมายความว่าตัวแปรตามไม่ได้เชื่อมต่อถึงกัน
• Homoskedasticity และความปกติของชุดตัวเลข

การใช้สหสัมพันธ์และการวิเคราะห์การถดถอย

มีสามกรณีหลักของการใช้วิธีนี้:

1. การทดสอบความสัมพันธ์แบบไม่เป็นทางการระหว่างปริมาณ ในกรณีนี้ผู้วิจัยกำหนดค่าของตัวแปรและค้นหาว่ามีผลต่อการเปลี่ยนแปลงในตัวแปรตามหรือไม่ ตัวอย่างเช่นคุณสามารถให้ปริมาณแอลกอฮอล์ที่แตกต่างกันและวัดความดันโลหิต ในกรณีนี้ผู้วิจัยรู้ว่าสิ่งแรกคือสาเหตุที่สองไม่ใช่ในทางกลับกัน การวิเคราะห์ความสัมพันธ์ - การถดถอยช่วยให้คุณสามารถตรวจสอบความสัมพันธ์เชิงเส้นที่มีสัดส่วนโดยตรงระหว่างตัวแปรทั้งสองนี้และหาสูตรที่อธิบายได้ ในกรณีนี้สามารถเปรียบเทียบค่าที่แสดงในหน่วยการวัดที่แตกต่างกันอย่างสิ้นเชิง
2. การค้นหาความสัมพันธ์ระหว่างสองตัวแปรโดยไม่ขยายความสัมพันธ์เชิงสาเหตุให้กับพวกเขา ในกรณีนี้ไม่มีความแตกต่างขนาดที่นักวิจัยเรียกขึ้นอยู่กับ ยิ่งกว่านั้นในความเป็นจริงมันอาจกลายเป็นว่าทั้งคู่ได้รับผลกระทบจากตัวแปรที่สามดังนั้นพวกเขาจึงเปลี่ยนตามสัดส่วน
3. การคำนวณค่าของปริมาณหนึ่งขึ้นอยู่กับปริมาณอื่น มันขึ้นอยู่กับสมการที่ตัวเลขที่รู้จักกันจะถูกแทนที่

ดังนั้นการวิเคราะห์ความสัมพันธ์เกี่ยวข้องกับการค้นหาการเชื่อมต่อ (ไม่ใช่สาเหตุ) ระหว่างตัวแปรและการวิเคราะห์การถดถอยอธิบายมันมักจะใช้ฟังก์ชั่นทางคณิตศาสตร์