Корелациона и регресијска анализа: пример, задаци, примена. Метода корелационе и регресијске анализе

Корелациона регресијска анализа - Ово је једна од најчешћих метода за проучавање односа бројчаних вредности. Његов главни циљ је проналажење односа двају параметара и његовог степена са накнадном изведбом једначине. На пример, имамо студенте који су положили испит из математике и енглеског језика. Помоћу корелације можемо утврдити да ли успех једног теста утиче на резултате у другом предмету. Што се тиче регресијске анализе, помаже вам да предвидите оцене из математике на основу поена постигнутих на испиту из енглеског језика и обрнуто.

Шта је корелациона карта?

Свака анализа започиње прикупљањем информација. Што је више, на крају је тачније резултат добијен. У горњем примеру имамо две дисциплине у којима студенти треба да положе испит. Њихова стопа успеха је процена. Корелационо-регресијска анализа показује да ли резултат једног предмета утиче на бодове постигнуте на другом испиту. Да би се одговорило на ово питање, потребно је паралелно анализирати оцене свих ученика. Али прво морате да одлучите о зависној варијабли. У овом случају није толико важно. Претпоставимо да се испит из математике одржао раније. Точке на њему су независна варијабла (одлажу се дуж апсцес). Енглески језик је на распореду касније. Стога су процјене засноване на њему зависна варијабла (цртане су дуж ординате). Што више овако добијени граф изгледа као равна линија, то је јача линеарна корелација између две изабране вредности. То значи да ће студенти математике вјероватно добити петице на испиту из енглеског језика.

Претпоставке и поједностављења

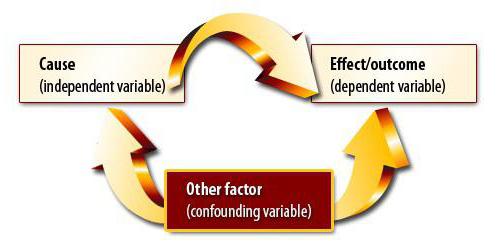
Метода корелацијске и регресијске анализе укључује проналажење узрочно-посљедичне везе. Међутим, на првој фази треба да схватите да промене у обе количине могу бити последица неке трећине, које истраживач још није узео у обзир. Такође може да постоји нелинеарна веза између променљивих, па добијање коефицијента једнаког нули није крај експеримента.

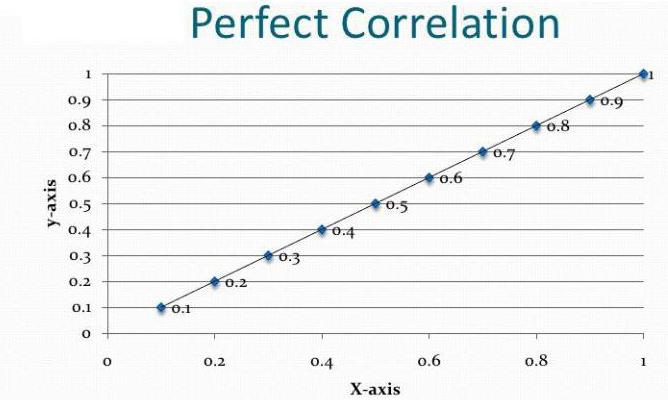
Пеарсонова линеарна корелација

Овај коефицијент се може користити под два услова. Прво - све вредности променљивих су рационални бројеви, друго - очекује се да се вредности пропорционално мењају. Овај коефицијент је увек између -1 и 1. Ако је већи од нуле, тада постоји директно пропорционална зависност, мање - обрнуто, једнака - ове вредности ни на који начин не утичу једна на другу. Способност израчунавања овог показатеља је основа корелационе и регресијске анализе. По први пут је овај коефицијент развио Карл Пеарсон на основу идеје Францисца Галтона.

Својства и мере опреза

Пеарсонов коефицијент корелације моћан је алат, али треба га користити и с опрезом. Следећа упозорења су у његовој употреби:

1. Пеарсонов коефицијент означава присуство или одсуство линеарног односа. Ту се не завршава корелацијско-регресијска анализа, може се испоставити да су променљиве међусобно повезане.
2. Морате бити опрезни у тумачењу вредности коефицијента. Може се пронаћи корелација између величине ноге и нивоа ИК.Али то не значи да један показатељ одређује други.
3. Пеарсонов коефицијент не говори ништа о узрочно-последичној вези између показатеља.

Спеарманов коефицијент корелације рангирања

Ако промена вредности једног показатеља доводи до повећања или смањења вредности другог, то значи да су оне повезане. Корелацијско-регресијска анализа, чији ће пример бити дат у даљем тексту, управо је повезана са таквим параметрима. Коефицијент рангирања омогућава вам да поједноставите израчуне.

Корелациона и регресијска анализа: пример

Претпоставимо да постоји процена ефикасности десет предузећа. Имамо два судије који им дају бодове. Корелациона и регресијска анализа предузећа у овом случају се не може извршити на основу линеарног Пеарсоновог коефицијента. Не занима нас однос оцењивања судија. Према речима судија, редови предузећа су важни.

Ова врста анализе има следеће предности:

• Непараметрични облик односа између испитиваних величина.
• Једноставност употребе, јер се редови могу приписати узлазном редоследу и опадајућем редоследу.

Једини захтев ове врсте анализе је потреба за претварањем изворних података.

Проблеми са апликацијом

Корелациона и регресијска анализа заснива се на следећим претпоставкама:

• Посматрања се сматрају независним (петоструки губитак „орла“ не утиче на резултат следећег пребацивања кованице).
• У корелацијској анализи обе варијабле се сматрају случајним. У регресији - само једна (зависна).
• Приликом испитивања хипотезе, мора се посматрати нормална дистрибуција. Промјена зависне варијабле треба бити иста за сваку вриједност на апсциси.
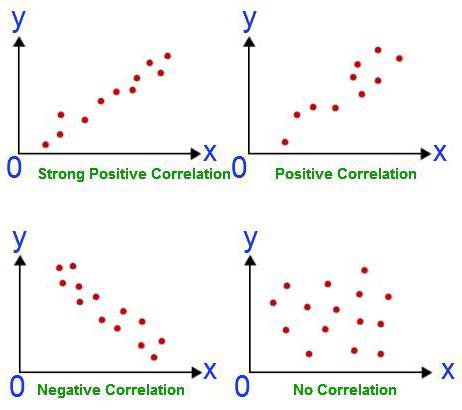
• Корелациони дијаграм само је први тест хипотезе о односу између два низа параметара, а не и коначни резултат анализе.

Зависност и узрочност

Претпоставимо да смо израчунали коефицијент корелације обима извоза и БДП-а. Показало се да је једнак модулу јединства. Да ли смо урадили корелацијску и регресијску анализу до краја? Наравно да не. Добивени резултат уопће не значи да се БДП може изразити извозом. Још нисмо доказали узрочно-посљедичну везу између показатеља. Корелацијско-регресијска анализа - предвиђање вредности једне променљиве на основу друге. Међутим, морате да схватите да често пуно фактора утиче на параметар. Извоз одређује БДП, али не само он. Постоје и други фактори. Овде постоји корелација и узрочно-посљедична веза, иако прилагођена другим компонентама бруто домаћег производа.

Друга ситуација је много опаснија. У Великој Британији је обављено истраживање које је показало да деца чији су родитељи пушили чешће буду починитељи кривичних дела. Овај закључак заснован је на снажној корелацији између показатеља. Али да ли је он тачан? Прво, зависност може бити обрнута. Родитељи би могли да пуше због стреса због чињенице да им се деца непрестано мијењају и крше закон. Друго, оба параметра могу бити последица трећег. Такве породице припадају ниским социјалним класама, које карактеришу оба проблема. Стога се на основу повезаности не може закључити да постоји узрочно-посљедична веза.

Зашто користити регресијску анализу?

Корелациона зависност укључује проналажење односа између количина. Каузални однос у овом случају остаје иза сцене. Задаци корелационе и регресијске анализе подударају се само у смислу потврђивања постојања односа између вредности две величине. Међутим, у почетку истраживач не обраћа пажњу на могућност узрочно-посљедичне везе. Регресијска анализа увек има две променљиве, од којих једна зависи. Одвија се у неколико фаза:

1. Одабир правог модела коришћењем методе најмање квадрата.
2. Извођење једначине која описује ефекат промене независне променљиве на другу.

На пример, ако проучавамо утицај старости на раст човека, тада регресијска анализа може да помогне у предвиђању промена током година.

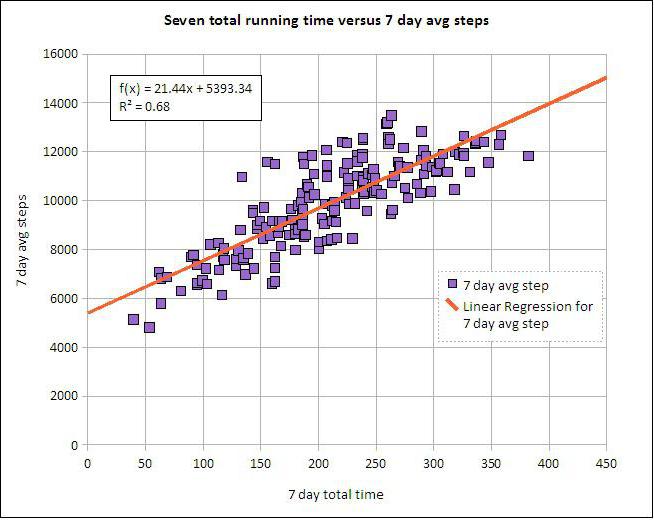
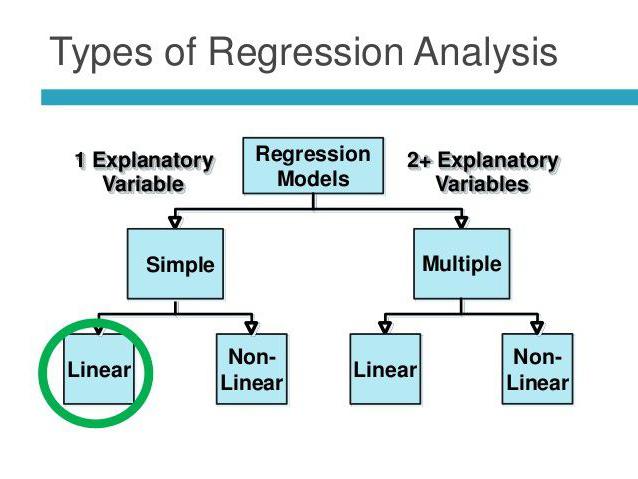
Линеарна и вишеструка регресија

Претпоставимо да су Кс и И две сродне променљиве. Регресијска анализа омогућава нам да предвидимо величину једног од њих на основу вредности другог. На пример, зрелост и старост су зависни симптоми. Однос међу њима одражава се линеарном регресијом. У ствари, Кс можете изразити И или обрнуто. Али често је само једна од регресијских линија тачна. Успех анализе у великој мери зависи од исправног одређивања независне променљиве. На пример, имамо два показатеља: принос и падавине. Из свакодневног искуства постаје јасно да прво зависи од другог, а не обрнуто.

Вишеструка регресија омогућава вам израчунавање непознате вредности на основу вредности три или више променљивих. На пример, принос пиринча по јутру земље зависи од квалитета зрна, плодности тла, ђубрива, температуре и падавина. Сви ови параметри утичу на укупни резултат. Да би се поједноставио модел, користе се следеће претпоставке:

• Веза између независних и утицајних карактеристика је линеарна.
• Мултиколинеарност је искључена. То значи да зависне променљиве нису међусобно повезане.
• Хомоскедастичност и нормалност низа бројева.

Употреба корелационе и регресијске анализе

Постоје три главна случаја употребе ове методе:

1. Испитивање повремених односа између количина. У овом случају, истраживач одређује вредности променљиве и открива да ли утичу на промену зависне променљиве. На пример, можете људима давати различите дозе алкохола и мерити њихов крвни притисак. У овом случају, истраживач сигурно зна да је прво узрок другог, а не обрнуто. Корелацијско-регресијска анализа омогућава вам да откријете директно пропорционални линеарни однос између ове две варијабле и добијете формулу која је описује. У овом случају, вредности изражене у потпуно различитим мерним јединицама могу се упоредити.
2. Проналажење односа између две варијабле без ширења узрочне везе на њих. У овом случају, нема разлике коју величину истраживач назива зависном. Штавише, у стварности се може испасти да на њих обоје утиче трећа променљива, па се сразмерно мењају.
3. Прорачун вредности једне количине на основу друге. Заснива се на једначини у којој су познати бројеви супституисани.

Дакле, корелациона анализа укључује проналажење везе (а не узрочно) између варијабли, а регресијска анализа објашњава то, често користећи математичку функцију.