Analisis korelasi dan regresi: contoh, tugas, permohonan. Kaedah analisis korelasi dan regresi

Analisis Regresi Korelasi - Ini adalah salah satu kaedah yang paling biasa untuk mengkaji hubungan antara nilai berangka. Matlamat utamanya ialah untuk mencari hubungan antara kedua-dua parameter dan darjahnya dengan derivasi seterusnya persamaan. Sebagai contoh, kami mempunyai pelajar yang telah lulus peperiksaan matematik dan Bahasa Inggeris. Kita boleh menggunakan korelasi untuk menentukan sama ada kejayaan satu ujian mempengaruhi hasil dalam subjek lain. Mengenai analisis regresi, ia membantu untuk meramalkan gred matematik berdasarkan mata yang dicetak dalam peperiksaan Bahasa Inggeris, dan sebaliknya.

Apakah carta korelasi?

Apa-apa analisis bermula dengan pengumpulan maklumat. Lebih-lebih lagi, lebih tepat hasil diperoleh pada akhirnya. Dalam contoh di atas, kami mempunyai dua disiplin di mana pelajar perlu lulus peperiksaan. Kadar kejayaan mereka adalah anggaran. Analisis regresi korelasi menunjukkan sama ada keputusan satu mata pelajaran mempengaruhi mata yang dicetak dalam peperiksaan kedua. Untuk menjawab soalan ini, adalah perlu untuk menganalisis penarafan semua pelajar selari. Tetapi pertama-tama anda perlu membuat keputusan tentang pemboleh ubah bergantung. Dalam kes ini, ia tidak begitu penting. Katakan ujian matematik berlaku lebih awal. Mata di atasnya adalah pembolehubah bebas (mereka ditunda sepanjang abscissa). Bahasa Inggeris berada di jadual kemudian. Oleh itu, anggaran berdasarkannya adalah pemboleh ubah bergantung (diperincikan di sepanjang ordinat). Semakin graf yang diperolehi kelihatan seperti garis lurus, semakin kuat korelasi linear antara dua nilai yang dipilih. Ini bermakna bahawa pelajar dalam matematik lebih cenderung mendapat keputusan peperiksaan Bahasa Inggeris.

Andaian dan Penyederhanaan

Kaedah analisis korelasi dan regresi melibatkan mencari hubungan kausal. Walau bagaimanapun, pada peringkat pertama, anda perlu memahami bahawa perubahan kedua-dua kuantiti boleh disebabkan oleh beberapa pertiga, yang belum diperhitungkan oleh penyelidik. Terdapat juga hubungan non-linear antara pemboleh ubah, oleh kerana itu, memperoleh koefisien sama dengan sifar bukanlah akhir eksperimen.

Korelasi linear Pearson

Pekali ini boleh digunakan tertakluk kepada dua syarat. Nilai pertama - semua pembolehubah adalah nombor rasional, kedua - dijangka bahawa nilai berubah secara proporsional. Pekali ini sentiasa di antara -1 dan 1. Jika ia lebih besar dari sifar, maka terdapat kebergantungan secara langsung proporsional, kurang - terbalik, sama - nilai ini tidak mempengaruhi satu sama lain dengan cara apapun. Keupayaan untuk mengira penunjuk ini adalah asas analisis korelasi dan regresi. Untuk pertama kalinya, pekali ini dikembangkan oleh Karl Pearson berdasarkan idea Francis Galton.

Hartanah dan Peringatan

Koefisien korelasi Pearson adalah alat yang berkuasa, tetapi ia juga harus digunakan dengan berhati-hati. Amaran berikut adalah dalam penggunaannya:

1. Koefisien Pearson menunjukkan kehadiran atau ketiadaan hubungan linear. Analisis regresi-korelasi tidak berakhir di sana, ia boleh berubah bahawa pembolehubah masih saling berkaitan.
2. Orang mesti berhati-hati dalam menafsirkan nilai pekali. Satu korelasi boleh didapati di antara saiz kaki dan tahap IQ.Tetapi ini tidak bermakna bahawa satu penunjuk menentukan yang lain.
3. Peksel Pearson tidak mengatakan apa-apa mengenai hubungan kausal antara penunjuk.

Pekali korelasi pangkat Spearman

Sekiranya perubahan dalam satu indikator membawa kepada peningkatan atau penurunan nilai yang lain, maka ini bermakna bahawa ia berkaitan. Analisis regresi korelasi, contohnya yang akan diberikan di bawah, adalah berkaitan dengan parameter sedemikian. Pekali kedudukan membolehkan anda memudahkan pengiraan.

Analisis korelasi dan regresi: satu contoh

Katakan bahawa terdapat penilaian terhadap keberkesanan sepuluh perusahaan. Kami mempunyai dua hakim yang memberi mereka mata. Analisis korelasi dan regresi syarikat dalam hal ini tidak dapat dilakukan berdasarkan pekali Pearson linear. Kami tidak berminat dalam hubungan antara penilaian hakim. Peringkat perusahaan mengikut hakim adalah penting.

Jenis analisis ini mempunyai kelebihan berikut:

• Bentuk hubungan nonparametrik antara kuantiti yang dikaji.
• Kemudahan penggunaan, kerana pangkat boleh dikaitkan baik dalam urutan menaik nilai dan urutan menurun.

Satu-satunya keperluan analisis jenis ini adalah keperluan untuk menukar data sumber.

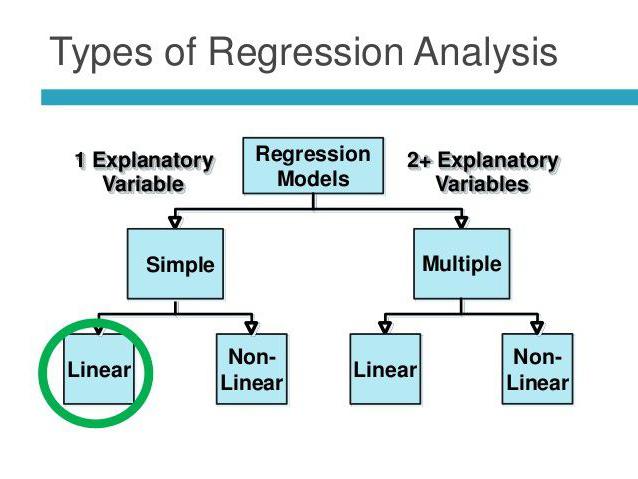
Masalah aplikasi

Analisis korelasi dan regresi berdasarkan andaian berikut:

• Pemerhatian dianggap bebas (kerugian lima kali ganda daripada "helang" tidak menjejaskan hasil flip duit syiling yang akan datang).
• Dalam analisis korelasi, kedua-dua pembolehubah dianggap rawak. Dalam regresi - hanya satu (bergantung).
• Apabila menguji hipotesis, pengedaran normal mesti diperhatikan. Perubahan dalam pemboleh ubah bergantung harus sama untuk setiap nilai pada abscissa.
• Gambar rajah korelasi adalah ujian pertama hipotesis tentang hubungan antara kedua-dua siri parameter, dan bukan hasil akhir analisis.

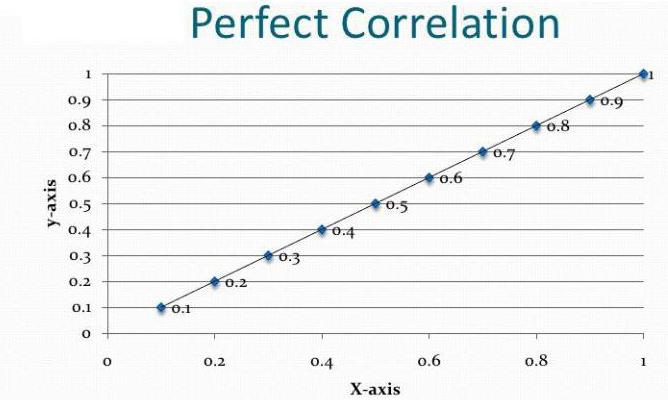
Ketergantungan dan penyebabnya

Katakan kita telah mengira pekali korelasi volum eksport dan KDNK. Ternyata sama dengan modulo perpaduan. Adakah kita telah melakukan analisis korelasi dan regresi sehingga akhir? Sudah tentu tidak. Hasil yang diperoleh tidak bermakna sama sekali bahawa KDNK boleh dinyatakan melalui eksport. Kami belum lagi membuktikan hubungan kausal antara petunjuk. Analisis regresi korelasi - meramalkan nilai-nilai satu pemboleh ubah berdasarkan yang lain. Walau bagaimanapun, anda perlu memahami bahawa sering banyak faktor mempengaruhi parameter. Eksport menentukan KDNK, tetapi bukan sahaja ia. Ada faktor lain. Di sini terdapat korelasi, dan hubungan kausal, walaupun diselaraskan untuk komponen lain dalam produk domestik kasar.

Keadaan lain adalah lebih berbahaya. Di UK, satu tinjauan dijalankan yang menunjukkan bahawa kanak-kanak yang merokok ibu bapa lebih sering pesalah. Kesimpulan ini adalah berdasarkan korelasi yang kuat antara penunjuk tersebut. Tetapi adakah dia betul? Pertama, pergantungan boleh berbalik. Ibu bapa boleh mula merokok kerana tekanan dari fakta bahawa anak-anak mereka sentiasa berubah dan melanggar undang-undang. Kedua, kedua-dua parameter mungkin disebabkan oleh yang ketiga. Keluarga sedemikian tergolong dalam kelas sosial yang rendah, yang dicirikan oleh kedua-dua masalah. Oleh itu, berdasarkan korelasi, tidak dapat disimpulkan bahawa terdapat hubungan kausal.

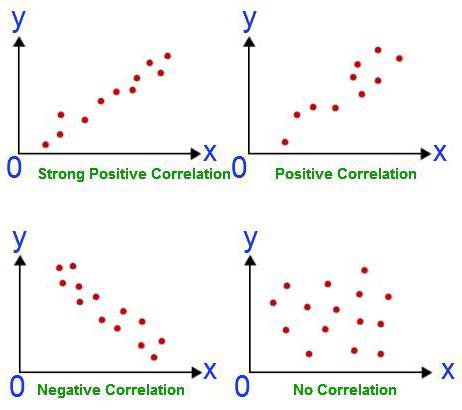
Mengapa menggunakan analisis regresi?

Ketergantungan korelasi melibatkan mencari hubungan antara kuantiti. Hubungan kausal dalam kes ini kekal di belakang tabir. Tugas analisis korelasi dan regresi bertepatan hanya dari segi mengesahkan kewujudan hubungan antara nilai dua kuantiti. Walau bagaimanapun, pada mulanya penyelidik tidak memberi perhatian kepada kemungkinan hubungan kausal. Analisis regresi sentiasa mempunyai dua pembolehubah, salah satunya adalah bergantung. Ia berlaku dalam beberapa peringkat:

1. Memilih model yang betul menggunakan kaedah kuasa sekurang-kurangnya.
2. Derivasi persamaan yang menerangkan kesan perubahan dalam pembolehubah bebas yang lain.

Sebagai contoh, jika kita mengkaji kesan usia ke atas pertumbuhan manusia, maka analisis regresi boleh membantu meramal perubahan selama bertahun-tahun.

Regresi linear dan berganda

Katakan X dan Y adalah dua pembolehubah yang berkaitan. Analisis regresi membolehkan kita untuk meramalkan magnitud salah satu daripada mereka berdasarkan nilai-nilai yang lain. Sebagai contoh, kematangan dan usia adalah gejala yang bergantung. Hubungan antara mereka digambarkan menggunakan regresi linear. Malah, anda boleh meluahkan X melalui Y atau sebaliknya. Tetapi selalunya hanya satu daripada garis regresi yang betul. Kejayaan analisis sebahagian besarnya bergantung kepada penentuan pembolehubah bebas yang betul. Sebagai contoh, kita mempunyai dua petunjuk: hasil dan pemendakan. Dari pengalaman sehari-hari, menjadi jelas bahawa yang pertama bergantung kepada yang kedua, dan bukan sebaliknya.

Regresi berganda membolehkan anda mengira nilai tidak diketahui berdasarkan nilai tiga atau lebih pembolehubah. Sebagai contoh, hasil beras per hektar tanah bergantung kepada kualiti bijirin, kesuburan tanah, baja, suhu, dan hujan. Semua parameter ini menjejaskan keseluruhan keputusan. Untuk mempermudah model, andaian berikut digunakan:

• Hubungan antara ciri-ciri bebas dan mempengaruhi adalah linear.
• Multicollinearity dikecualikan. Ini bermakna pembolehubah bergantung tidak saling berkaitan.
• Homosekediti dan normalisasi siri nombor.

Penggunaan analisis korelasi dan regresi

Terdapat tiga kes utama menggunakan kaedah ini:

1. Menguji hubungan santai antara kuantiti. Dalam kes ini, penyelidik menentukan nilai-nilai pemboleh ubah dan mendapati sama ada ia mempengaruhi perubahan dalam pembolehubah bergantung. Contohnya, anda boleh memberi orang alkohol yang berbeza dan mengukur tekanan darah mereka. Dalam kes ini, penyelidik tahu pasti bahawa yang pertama adalah punca kedua, dan bukan sebaliknya. Analisis regresi korelasi membolehkan anda untuk mengesan hubungan linear lurus secara proporsional antara kedua-dua pembolehubah tersebut dan memperoleh formula yang menggambarkannya. Dalam kes ini, nilai yang dinyatakan dalam unit pengukuran yang sama sekali berbeza boleh dibandingkan.
2. Mencari hubungan antara dua pembolehubah tanpa memanjangkan hubungan kausal dengan mereka. Dalam kes ini, tidak ada perbezaan saiz yang bergantung kepada penyelidik. Lebih-lebih lagi, pada hakikatnya, ia mungkin berubah bahawa kedua-dua mereka dipengaruhi oleh pembolehubah ketiga, oleh itu mereka berubah secara proporsional.
3. Pengiraan nilai satu kuantiti berdasarkan kepada yang lain. Ia didasarkan pada persamaan di mana bilangan diketahui digantikan.

Oleh itu, analisis korelasi melibatkan mencari sambungan (bukan kausal) antara pembolehubah, dan analisis regresi menerangkannya, sering menggunakan fungsi matematik.