Korelācijas un regresijas analīze: piemērs, uzdevumi, pielietojums. Korelācijas un regresijas analīzes metode

Korelācijas regresijas analīze - Šī ir viena no visizplatītākajām metodēm, lai izpētītu sakarību starp skaitliskajām vērtībām. Tās galvenais mērķis ir atrast saistību starp diviem parametriem un tā pakāpi ar sekojošu vienādojuma atvasināšanu. Piemēram, mums ir studenti, kuri ir nokārtojuši matemātikas un angļu valodas eksāmenu. Mēs varam izmantot korelāciju, lai noteiktu, vai viena testa panākumi ietekmē cita subjekta rezultātus. Attiecībā uz regresijas analīzi tas palīdz paredzēt matemātikas atzīmes, pamatojoties uz angļu valodas eksāmenā iegūtajiem punktiem, un otrādi.

Kas ir korelācijas diagramma?

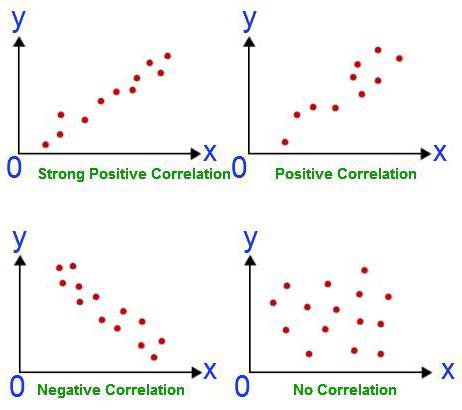
Jebkura analīze sākas ar informācijas vākšanu. Jo vairāk tas ir, jo precīzāk tiek iegūts rezultāts beigās. Iepriekš minētajā piemērā mums ir divas disciplīnas, kurās studentiem jānokārto eksāmens. Viņu panākumu līmenis ir aptuvens. Korelācijas-regresijas analīze parāda, vai viena subjekta rezultāts ietekmē otrajā eksāmenā iegūtos punktus. Lai atbildētu uz šo jautājumu, paralēli jāanalizē visu studentu vērtējumi. Bet vispirms jums jāizlemj par atkarīgo mainīgo. Šajā gadījumā tas nav tik svarīgi. Pieņemsim, ka matemātikas eksāmens notika agrāk. Punkti uz tā ir neatkarīgs mainīgais (tie tiek atlikti gar abscisu). Angļu valoda ir iekļauta grafikā vēlāk. Tāpēc aprēķini, kas balstīti uz to, ir atkarīgs mainīgais lielums (tiek attēloti gar ordinātu). Jo vairāk šādi iegūtais grafiks izskatās kā taisna līnija, jo spēcīgāka ir abu izvēlēto vērtību lineārā korelācija. Tas nozīmē, ka matemātikas studenti angļu valodas eksāmenā biežāk saņem piecus.

Pieņēmumi un vienkāršojumi

Korelācijas un regresijas analīzes metode ietver cēloņsakarības atrašanu. Tomēr pirmajā posmā jums ir jāsaprot, ka izmaiņas abos daudzumos var notikt kāda trešā dēļ, ko pētnieks vēl nav ņēmis vērā. Starp mainīgajiem var būt arī nelineāras attiecības, tāpēc koeficienta iegūšana, kas ir vienāda ar nulli, nav eksperimenta beigas.

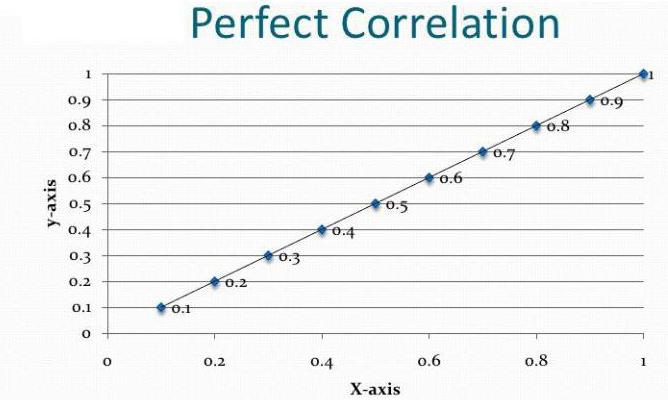
Pīrsona lineārā korelācija

Šo koeficientu var izmantot, ievērojot divus nosacījumus. Pirmais - visas mainīgo vērtības ir racionāli skaitļi, otrais - ir paredzams, ka vērtības mainās proporcionāli. Šis koeficients vienmēr ir no -1 līdz 1. Ja tas ir lielāks par nulli, tad pastāv tieši proporcionāla atkarība, mazāka - apgriezti vienāda - šīs vērtības nekādā veidā neietekmē viena otru. Spēja aprēķināt šo rādītāju ir korelācijas un regresijas analīzes pamatā. Pirmo reizi šo koeficientu izstrādāja Kārlis Pīrsons, pamatojoties uz Fransisa Galtona ideju.

Īpašības un brīdinājumi

Pīrsona korelācijas koeficients ir spēcīgs instruments, taču tas arī jālieto piesardzīgi. Tiek izmantoti šādi brīdinājumi:

1. Pīrsona koeficients norāda uz lineāras attiecības esamību vai neesamību. Korelācijas-regresijas analīze ar to nebeidzas, var izrādīties, ka mainīgie tomēr ir savstarpēji saistīti.
2. Interpretējot koeficienta vērtību, jābūt uzmanīgam. Var atrast korelāciju starp kājas izmēru un IQ līmeni.Bet tas nenozīmē, ka viens rādītājs nosaka citu.
3. Pīrsona koeficients neko nesaka par cēloņsakarību starp rādītājiem.

Spīrmena pakāpes korelācijas koeficients

Ja viena rādītāja vērtības izmaiņas izraisa cita vērtības palielināšanos vai samazināšanos, tas nozīmē, ka tās ir saistītas. Ar šādiem parametriem ir precīzi saistīta korelācijas-regresijas analīze, kuras piemērs tiks sniegts turpmāk. Ranga koeficients ļauj vienkāršot aprēķinus.

Korelācijas un regresijas analīze: piemērs

Pieņemsim, ka ir novērtēts desmit uzņēmumu efektivitāte. Mums ir divi tiesneši, kuri viņiem piešķir punktus. Uzņēmuma korelācijas un regresijas analīzi šajā gadījumā nevar veikt, pamatojoties uz lineāro Pīrsona koeficientu. Mūs neinteresē tiesnešu vērtējumu attiecības. Uzņēmumu svari, pēc tiesnešu uzskatiem, ir svarīgi.

Šim analīzes veidam ir šādas priekšrocības:

• Neparametriskā attiecību forma starp pētītajiem lielumiem.
• Lietošanas ērtums, jo rindas var attiecināt gan vērtības augošā secībā, gan dilstošā secībā.

Vienīgā šāda veida analīzes prasība ir nepieciešamība konvertēt avota datus.

Lietošanas problēmas

Korelācijas un regresijas analīzes pamatā ir šādi pieņēmumi:

• Novērojumi tiek uzskatīti par neatkarīgiem (piecas reizes lielāks “ērgļa” zaudējums neietekmē nākamās monētas uzsitiena rezultātu).
• Korelācijas analīzē abi mainīgie tiek uzskatīti par nejaušiem. Regresijā - tikai viens (atkarīgs).
• Pārbaudot hipotēzi, jāievēro normāls sadalījums. Atkarīgā mainīgā izmaiņām jābūt vienādām katrai abscisa vērtībai.
• Korelācijas diagramma ir tikai pirmais hipotēzes par saistību starp abām parametru sērijām pārbaude, nevis analīzes galīgais rezultāts.

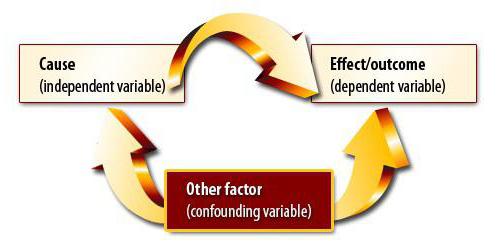
Atkarība un cēloņsakarība

Pieņemsim, ka mēs esam aprēķinājuši eksporta apjoma un IKP korelācijas koeficientu. Tas izrādījās vienāds ar vienotības modulo. Vai mēs esam izdarījuši korelācijas un regresijas analīzi līdz galam? Protams, ka nē. Iegūtais rezultāts nenozīmē, ka IKP var izteikt ar eksporta palīdzību. Mēs vēl neesam pierādījuši cēloņsakarību starp rādītājiem. Korelācijas-regresijas analīze - viena mainīgā vērtību prognozēšana, pamatojoties uz citu. Tomēr jums jāsaprot, ka parametru bieži ietekmē ļoti daudz faktoru. Eksports nosaka IKP, bet ne tikai to. Ir arī citi faktori. Šeit pastāv korelācija un cēloņsakarība, kaut arī koriģēta attiecībā uz citām iekšzemes kopprodukta sastāvdaļām.

Cita situācija ir daudz bīstamāka. Lielbritānijā tika veikta aptauja, kas parādīja, ka bērni, kuru vecāki smēķēja, biežāk bija likumpārkāpēji. Šā secinājuma pamatā ir cieša korelācija starp rādītāju. Bet vai viņš ir pareizs? Pirmkārt, atkarība varētu būt apgriezta. Vecāki varēja sākt smēķēt stresa dēļ no tā, ka viņu bērni pastāvīgi nonāk pārmaiņas un pārkāpj likumu. Otrkārt, abi parametri var būt saistīti ar trešo. Šādas ģimenes pieder zemām sociālajām klasēm, kurām raksturīgas abas problēmas. Tāpēc, pamatojoties uz korelāciju, nevar secināt, ka pastāv cēloņsakarība.

Kāpēc izmantot regresijas analīzi?

Korelācijas atkarība ietver attiecību atrašanu starp daudzumiem. Cēloņsakarība šajā gadījumā paliek aizkulisēs. Korelācijas un regresijas analīzes uzdevumi sakrīt tikai ar nosacījumu, ka tiek apstiprināta saistība starp divu lielumu vērtībām. Tomēr sākotnēji pētnieks nepievērš uzmanību cēloņsakarības iespējamībai. Regresijas analīzē vienmēr ir divi mainīgie, no kuriem viens ir atkarīgs. Tas notiek vairākos posmos:

1. Pareizā modeļa izvēle, izmantojot vismazāko kvadrātu metodi.
2. Vienādojuma atvasināšana, kas apraksta neatkarīga mainīgā izmaiņu ietekmi uz citu.

Piemēram, ja mēs pētām vecuma ietekmi uz cilvēka augšanu, tad regresijas analīze var palīdzēt prognozēt izmaiņas gadu gaitā.

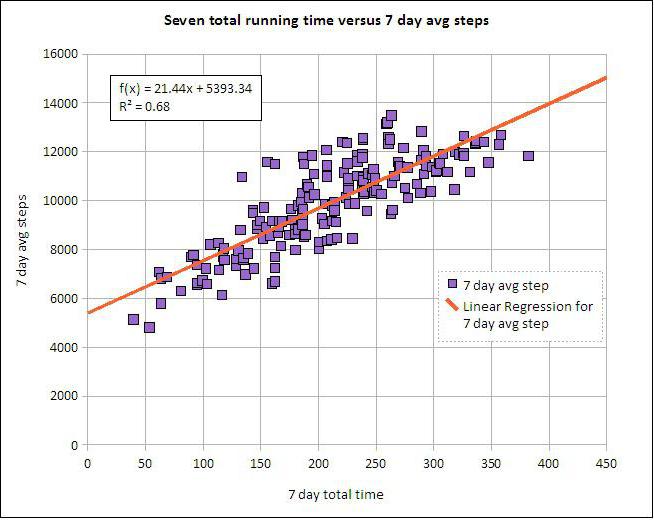
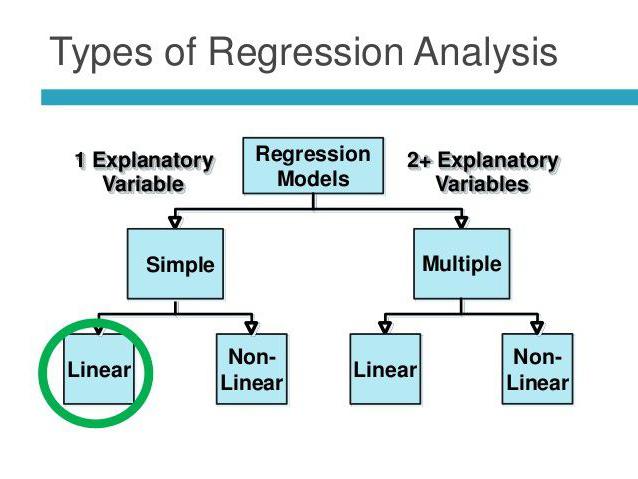
Lineārā un daudzkārtīgā regresija

Pieņemsim, ka X un Y ir divi saistīti mainīgie. Regresijas analīze ļauj prognozēt viena no tām lielumu, pamatojoties uz otra vērtību. Piemēram, briedums un vecums ir atkarīgi simptomi. Attiecības starp tām tiek atspoguļotas, izmantojot lineāru regresiju. Faktiski jūs varat izteikt X caur Y vai otrādi. Bet bieži vien viena no regresijas līnijām ir pareiza. Analīzes panākumi lielā mērā ir atkarīgi no pareiza neatkarīgā mainīgā noteikšanas. Piemēram, mums ir divi rādītāji: raža un nokrišņi. No ikdienas pieredzes kļūst skaidrs, ka pirmais ir atkarīgs no otrā, nevis otrādi.

Vairākkārtēja regresija ļauj aprēķināt nezināmu vērtību, pamatojoties uz trīs vai vairāku mainīgo lielumiem. Piemēram, rīsu raža uz vienu zemes hektāru ir atkarīga no graudu kvalitātes, augsnes auglības, mēslošanas līdzekļiem, temperatūras un nokrišņiem. Visi šie parametri ietekmē kopējo rezultātu. Modeļa vienkāršošanai tiek izmantoti šādi pieņēmumi:

• Saistība starp neatkarīgajām un ietekmējošajām īpašībām ir lineāra.
• Daudzkoloģiskums ir izslēgts. Tas nozīmē, ka atkarīgie mainīgie nav savstarpēji saistīti.
• Skaitļu virkņu homoskedasticitāte un normalitāte.

Korelācijas un regresijas analīzes izmantošana

Šīs metodes izmantošanai ir trīs galvenie gadījumi:

1. Gadījumu attiecību pārbaude starp daudzumiem. Šajā gadījumā pētnieks nosaka mainīgā lielumus un noskaidro, vai tie ietekmē mainīgā lielumu mainīgajā. Piemēram, jūs varat dot cilvēkiem dažādas alkohola devas un izmērīt asinsspiedienu. Šajā gadījumā pētnieks droši zina, ka pirmais ir otrā cēlonis, nevis otrādi. Korelācijas-regresijas analīze ļauj noteikt tieši proporcionālu lineāru saikni starp šiem diviem mainīgajiem un iegūt formulu, kas to raksturo. Šajā gadījumā var salīdzināt vērtības, kas izteiktas pilnīgi dažādās mērvienībās.
2. Attiecību atrašana starp diviem mainīgajiem, nepaplašinot cēloņsakarību ar tiem. Šajā gadījumā nav atšķirības, kādu izmēru pētnieks sauc par atkarīgu. Turklāt patiesībā var izrādīties, ka trešais mainīgais ietekmē tos abus, tāpēc tie mainās proporcionāli.
3. Viena daudzuma vērtību aprēķināšana, pamatojoties uz citu. Tā pamatā ir vienādojums, kurā zināmie skaitļi tiek aizstāti.

Tādējādi korelācijas analīze ietver saiknes (nevis cēloņsakarības) atrašanu starp mainīgajiem, un regresijas analīze to izskaidro, bieži izmantojot matemātisko funkciju.