Betydningsniveauet i statistikker er en vigtig indikator, der afspejler graden af tillid til nøjagtigheden og sandheden af de modtagne (forudsagte) data. Konceptet er meget udbredt inden for forskellige områder: fra udførelse af sociologisk forskning til statistisk test af videnskabelige hypoteser.

definition
Niveauet for statistisk signifikans (eller statistisk signifikant resultat) viser, hvad der er sandsynligheden for en tilfældig forekomst af de studerede indikatorer. Fænomenets generelle statistiske betydning udtrykkes ved koefficienten p-værdi (p-niveau). I ethvert eksperiment eller observation er det sandsynligt, at de opnåede data skyldes prøveudtagningsfejl. Dette gælder især for sociologi.
Det vil sige, en statistik er statistisk signifikant, hvis sandsynlighed for utilsigtet forekomst er ekstremt lille eller har en tendens til ekstremer. Ekstrem betragtes i denne sammenhæng graden af afvigelse af statistik fra nullhypotesen (en hypotese, der kontrolleres for overensstemmelse med de opnåede eksempeldata). I videnskabelig praksis vælges signifikansniveauet inden dataindsamling, og som regel er dens koefficient 0,05 (5%). For systemer, hvor nøjagtige værdier er ekstremt vigtige, kan denne indikator være 0,01 (1%) eller mindre.
sygehistorie
Begrebet betydningsniveau blev introduceret af den britiske statistiker og genetiker Ronald Fisher i 1925, da han udviklede en metode til test af statistiske hypoteser. Når man analyserer en proces, er der en vis sandsynlighed for visse fænomener. Vanskeligheder opstår, når man arbejder med små (eller ikke indlysende) procentvise sandsynligheder, der falder ind under begrebet "målefejl."
Når de arbejdede med statistikker, der ikke er specifikke nok til at verificere, stod forskere over for problemet med nulhypotesen, som "forstyrrer" med små mængder. Fisher foreslog at definere for sådanne systemer sandsynlighed for begivenheder 5% (0,05) som en praktisk selektiv skive, så du kan afvise nulhypotesen i beregningerne.
Indførelsen af en fast koefficient
I 1933 anbefalede forskere Jerzy Neumann og Egon Pearson i deres værker på forhånd (før dataindsamling) for at etablere et vist niveau af betydning. Eksempler på brugen af disse regler er tydeligt synlige under valget. Antag, at der er to kandidater, hvoraf den ene er meget populær, og den anden er lidt kendt. Det er klart, at den første kandidat vinder valget, og chancerne for den anden tendens til at være nul. De stræber efter - men ikke lige: der er altid sandsynligheden for force majeure, sensationel information, uventede beslutninger, der kan ændre de forudsagte valgresultater.
Neumann og Pearson var enige om, at Fishers foreslåede signifikansniveau på 0,05 (betegnet med symbolet α) er mest praktisk. Imidlertid modsatte Fisher sig selv i 1956 fastlæggelsen af denne værdi. Han mente, at niveauet af a skulle fastlægges i overensstemmelse med specifikke omstændigheder. For eksempel er det i partikelfysik 0,01.

Signifikansniveau på p
Udtrykket p-værdi blev først brugt i Brownleys arbejde i 1960. P-niveau (p-værdi) er en indikator, der er omvendt relateret til sandheden i resultaterne. Den højeste koefficient p-værdi svarer til det laveste niveau af tillid til prøven af afhængighed mellem variablerne.
Denne værdi afspejler sandsynligheden for fejl, der er forbundet med fortolkningen af resultaterne. Antag, at p-niveau = 0,05 (1/20). Det viser sandsynligheden for fem procent, at forholdet mellem de variabler, der findes i prøven, kun er et tilfældigt træk ved prøven.Det vil sige, hvis denne afhængighed er fraværende, kan man med gentagne sådanne eksperimenter i gennemsnit i hver tyvende undersøgelse forvente den samme eller større afhængighed mellem variablerne. Ofte betragtes p-niveauet som "acceptabel margen" for fejlniveauet.
For øvrigt afspejler p-værdi muligvis ikke det reelle forhold mellem variablerne, men viser kun en vis gennemsnitlig værdi inden for antagelserne. Især afhænger den endelige analyse af dataene af de valgte værdier for denne koefficient. Med et p-niveau = 0,05 vil der være nogle resultater og med en koefficient på 0,01 andre.

Test af statistiske hypoteser
Niveauet for den statistiske betydning er især vigtigt, når man tester hypoteser. For eksempel, når man beregner en tosidet test, er afvisningsområdet opdelt ligeligt i begge ender af prøvefordelingen (i forhold til nulkoordinaten), og sandheden i dataene beregnes.
Antag, at det ved overvågning af en bestemt proces (fænomen) viste sig, at den nye statistiske information indikerer små ændringer i forhold til tidligere værdier. Desuden er forskellene i resultaterne små, ikke indlysende, men vigtige for undersøgelsen. Dilemmaet opstår inden specialisten: finder de virkelig ændringer sted, eller er disse prøveudtagningsfejl (unøjagtige målinger)?
I dette tilfælde bruges eller afvises nulhypotesen (alt tilskrives en fejl, eller ændringen i systemet genkendes som en fait accompli). Processen med at løse problemet er baseret på forholdet mellem total statistisk signifikans (p-værdi) og signifikansniveau (α). Hvis p-niveauet <α, afvises nulhypotesen. Jo mindre p-værdi, desto mere signifikant er teststatistikken.
Brugte værdier
Betydningsniveauet afhænger af det materiale, der analyseres. I praksis bruges følgende faste værdier:
- a = 0,1 (eller 10%);
- a = 0,05 (eller 5%);
- a = 0,01 (eller 1%);
- a = 0,001 (eller 0,1%).
Jo mere nøjagtige beregningerne kræves, jo lavere bruges koefficienten α. Naturligvis kræver statistiske prognoser inden for fysik, kemi, medicinalvarer, genetik større nøjagtighed end inden statsvidenskab, sociologi.

Tærskler af relevans i specifikke områder
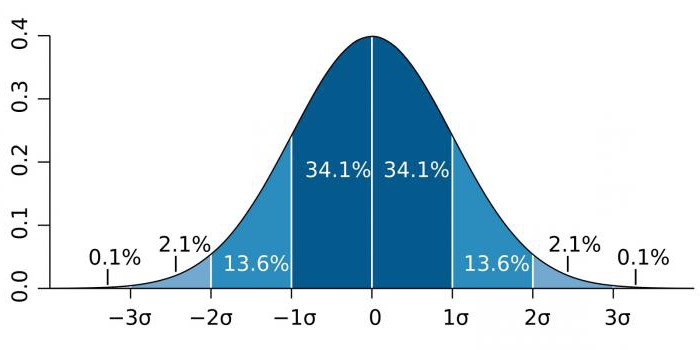
I områder med høj præcision, såsom partikelfysik og fremstillingsaktiviteter, udtrykkes statistisk betydning ofte som forholdet mellem standardafvigelsen (betegnet med sigma-koefficienten - σ) i forhold til den normale sandsynlighedsfordeling (Gaussisk distribution). σ er en statistisk indikator, der bestemmer spredningen af værdier for en bestemt værdi i forhold til matematiske forventninger. Bruges til at kortlægge sandsynligheden for begivenheder.
Afhængig af vidensområdet varierer koefficienten σ meget. For eksempel, når man forudsiger eksistensen af Higgs boson, er parameteren σ fem (σ = 5), hvilket svarer til værdien p-værdi = 1 / 3,5 millioner. I studier af genomer kan signifikansniveauet være 5 × 10-8der ikke er usædvanligt for dette område.
effektivitet
Husk, at koefficienterne a og p-værdien ikke er nøjagtige egenskaber. Uanset betydningsniveauet i statistikken over det studerede fænomen er det ikke et ubetinget grundlag for at acceptere hypotesen. Jo mindre værdien af α er, jo større er chancen for, at den etablerede hypotese er betydelig. Der er dog en risiko for fejl, hvilket reducerer undersøgelsens statistiske magt (betydning).
Forskere, der udelukkende fokuserer på statistisk signifikante resultater, kan få fejlagtige konklusioner. Samtidig er det vanskeligt at dobbeltkontrol deres arbejde, da de bruger antagelser (som faktisk er α og p-værdi). Derfor anbefales det altid sammen med beregningen af statistisk signifikans at bestemme en anden indikator - størrelsen af den statistiske effekt. Størrelsen af en effekt er et kvantitativt mål for effektens styrke.
