"Stokastisk" er et ord, som fysikere, matematikere og andre forskere bruger til at beskrive processer, der har et element af chance. Dets oprindelse er gammelgræsk. Oversat betyder det "i stand til at gætte."
Betydning af ordet "stokastisk"

"Stokastisk" er et koncept, der bruges inden for mange forskellige videnskabelige områder. Det betyder tilfældighed, tilfældighed, usikkerhed omkring noget. I Aristoteles etik (hans skulpturelle portræt er præsenteret ovenfor) er begrebet "stokastisk" en definition, der henviser til evnen til at gætte. Naturligvis brugte matematikere det på det grundlag, at tilfældet indtræffer lige når det er nødvendigt at gætte. Ordet "stokastisk" er et begreb, der i den nye internationale ordbog defineres som "formodet."
Det kan således bemærkes, at den tekniske betydning af dette koncept ikke nøjagtigt svarer til dets ordforråd (leksikale) betydning. Nogle forfattere bruger udtrykket "stokastisk proces" som et synonym for udtrykket "tilfældig proces".
Stokastisitet i matematik

Brugen af dette udtryk i matematik er i øjeblikket udbredt. For eksempel er der et sådant begreb i sandsynlighedsteori som den stokastiske proces. Dets resultat kan ikke bestemmes af den indledende tilstand af dette system.
Brugen i matematik af begrebet "stokastisitet" tilskrives værkerne fra Vladislav Bortskevich. Det var han, der brugte udtrykket i betydningen "fremsatte hypoteser." I matematik, især i et sådant afsnit af denne videnskab som sandsynlighedsteori, spiller området tilfældig forskning en vigtig rolle. Der er for eksempel sådan en ting som en stokastisk matrix. Kolonnerne eller rækkerne i denne matrix føjer op til en.
Stokastisk matematik (finansiel)
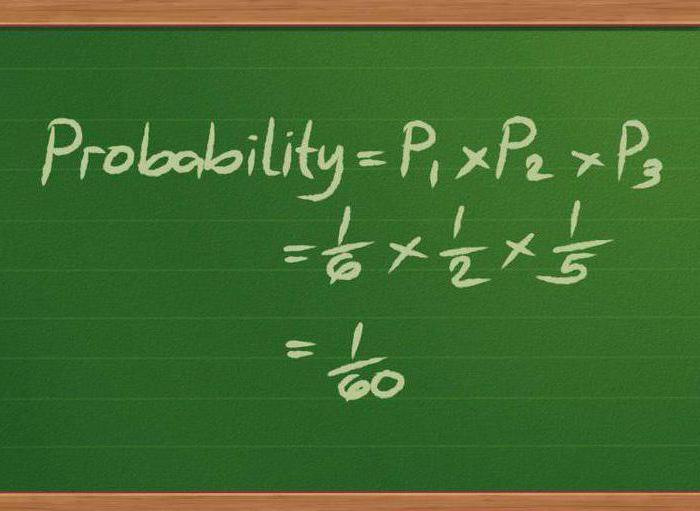
Dette afsnit af matematik analyserer økonomiske strukturer, der fungerer under usikkerhedsforhold. Det er designet til at finde de mest rationelle metoder til styring af finansielle aktiver og strukturer under hensyntagen til faktorer som stokastisk udvikling, risiko, tid osv.
I videnskab er det sædvanligt at skelne mellem følgende strukturer og objekter, der bruges i finansiel matematik som helhed:
- virksomheder (for eksempel virksomheder);
- enkeltpersoner;
- formidlende strukturer (pensionskasser, banker);
- finansielle markeder.
Hovedformålet med studiet af stokastisk økonomisk matematik er netop det sidste af dem. Dette afsnit er baseret på sådanne discipliner som statistik over tilfældige processer, teori om tilfældige processer osv.
På nuværende tidspunkt, selv folk langt fra videnskab, er det velkendt fra adskillige nyheder og publikationer i medierne, at værdierne på de såkaldte globale finansielle indekser (for eksempel Dow Jones-indekset), aktiekurserne ændrer sig tilfældigt. L. Bachelier gjorde det første forsøg på at beskrive ved hjælp af matematik udviklingen i aktiekurserne. Hans stokastiske metode er baseret på sandsynlighedsteori. L. Bacheliers afhandling, der præsenterer dette forsøg, blev offentliggjort i 1900. Forskeren har bevist den formel, der i øjeblikket er kendt som dagsværdiformlen for opkaldsmuligheder. Det afspejler den stokastiske sandsynlighed.
Vigtige ideer, der efterfølgende førte til fremkomsten af en effektiv markedsteori blev præsenteret i arbejdet med M. Kendall, der blev offentliggjort i 1953. Dette papir behandler spørgsmålet om aktiekursdynamik. Forskeren beskriver det ved hjælp af stokastiske processer.
Stokastisitet i fysik
Tak til fysikere E. Fermi, S. Ulam, N. Metropolis og D.Neumann er vidt anvendt Monte Carlo-metode. Navnet kommer fra et kasino beliggende i den samme by i et land som Monaco. Det var her, onkel Ulam lånte penge til spillet. At bruge arten af gentagelse og chance for at studere processer ligner det, der sker i et kasino.

Ved anvendelse af denne modelleringsmetode søges først en probabilistisk analog. Før dette blev modellering udført i den modsatte retning: den blev brugt til at verificere resultatet af det tidligere deterministiske problem. Selvom der eksisterede lignende tilgange før opdagelsen af Monte Carlo-metoden, var de ikke populære og generelle.
Enrico Fermi i 1930 anvendte stokastiske teknikker til at beregne egenskaberne for neutronen, som netop var blevet opdaget på det tidspunkt. Monte Carlo-metoder blev senere brugt, da man arbejdede på Manhattan-projektet, selvom computere på det tidspunkt var betydeligt begrænsede. Af denne grund blev de kun udbredt efter computere dukkede op.
Stokastiske signaler
Regelmæssige og stokastiske signaler har forskellige bølgeformer. Hvis vi måler sidstnævnte, får vi svingninger, der har en ny form, som er anderledes end den foregående, men viser en vis lighed i væsentlige funktioner. Et eksempel på et stokastisk signal er optagelsen af havbølgesvingninger.
Hvorfor er det nødvendigt at tale om disse temmelig usædvanlige signaler? Faktum er, at de i studiet af automatiske systemer er endnu mere almindelige end forudsagt.
Stokastisitet og kunstig intelligens
Stokastiske kunstige intelligensprogrammer arbejder ved hjælp af probabilistiske metoder. Algoritmer såsom stokastisk optimering eller neurale netværk kan nævnes som et eksempel. Det samme gælder for simuleret annealing og genetiske algoritmer. I alle disse tilfælde kan stokastisitet være indeholdt i problemet som sådan eller ved at planlægge noget under betingelse af usikkerhed. Det deterministiske miljø for et modelleringsmiddel er enklere end stokastisk.

Så som vi ser, bruges begrebet interesse for os inden for mange videnskabelige områder. Vi har kun opført og karakteriseret de vigtigste områder for dens anvendelse. Undersøgelsen af alle disse processer, ser du, er meget vigtig og relevant. Det er grunden til, at begrebet interesse for os sandsynligvis vil blive brugt i lang tid i videnskaben.








