Từ ghép "ngoại suy" bao gồm hai từ đơn giản. Đầu tiên trong tiếng Latin có nghĩa là thêm và có nghĩa là "bên ngoài", "cho", "bên ngoài". Thứ hai trong cùng một tiếng Latin có vẻ lịch sự và có nghĩa là "thay đổi", "duỗi thẳng", "trơn tru". Nói chung, phép ngoại suy có thể được định nghĩa là một giá trị bên ngoài hai điểm đã cho. Nó được coi là một đánh giá về những gì được trích xuất từ các sự kiện đã biết mở rộng dữ liệu trong một khu vực không xác định để đi đến kết quả dự định. Khái niệm này cũng có thể được quy cho dự đoán về hình ảnh của tương lai, giả định sự thật của xu hướng hiện tại và quá khứ.
Phương pháp ngoại suy giả định rằng dữ liệu hoặc quan sát trong tương lai sẽ tiếp tục tương tự. Do đó, kết quả trong tương lai có thể được dự đoán. Nó có thể được coi là một giả thuyết toán học. Phép ngoại suy sử dụng dữ liệu và sự kiện của một tình huống cụ thể và đưa ra dự đoán về những gì có thể xảy ra cuối cùng.
Lịch sử ngoại suy

Phương pháp này thường được gọi là phép ngoại suy Richardson hoặc phương pháp Romberg. Nhưng điều này không hoàn toàn chính xác, vì trong nhiều thế kỷ đã có những phương pháp số tương tự để giải quyết những vấn đề như vậy. Do đó, Richardson h2 nổi tiếng (ngoại suy cho một giải pháp số) không phải là lần đầu tiên. Một phương pháp tương tự đã được áp dụng trong tính toán của Huygens vào đầu năm 1654. Bản thân thuật ngữ "ngoại suy" lần đầu tiên được Thomas D. Clareson đặt ra vào năm 1959 trong một cuốn sách về khoa học và viễn tưởng.
Các phương pháp ngoại suy có thể được hiểu là sự mở rộng của dữ liệu hoặc quy trình, cho thấy rằng một quy trình tương tự sẽ được áp dụng bên ngoài chúng. Phép ngoại suy là một khái niệm quan trọng được sử dụng không chỉ trong toán học, mà còn trong các lĩnh vực khác, như xã hội học, tâm lý học, dự báo. Ví dụ, một người lái xe thường ngoại suy các điều kiện lái xe ngoài tầm nhìn của anh ta. Phép ngoại suy có thể được quy cho một phương thức trong đó các giá trị dữ liệu được coi là các điểm x1, x2 ..., xn và sau đó giá trị đạt đến giới hạn của một phạm vi các điểm nhất định.
Lợi ích của việc sử dụng:
- Một phương pháp dự báo đơn giản.
- Không có nhiều dữ liệu được yêu cầu.
- Phân tích nhanh và rẻ.
Phương pháp tồn tại trong thống kê. Nếu bất kỳ giá trị nào được định kỳ loại bỏ, câu trả lời sẽ tiếp cận điểm dữ liệu tiếp theo. Một ví dụ về phương pháp ngoại suy là dự báo thời tiết, kiểm tra nền tảng của dữ liệu và ngoại suy mô hình dự đoán của tương lai. Một ví dụ đơn giản hơn nữa, nếu bạn có thông tin về Chủ nhật, Thứ Hai và Thứ Ba, bạn có thể ngoại suy vào Thứ Tư hoặc Thứ Năm.
Nhược điểm của việc sử dụng phép ngoại suy:
- Không đáng tin cậy, nếu có biến động đáng kể trong dữ liệu lịch sử.
- Giả định rằng xu hướng trong quá khứ sẽ tiếp tục trong tương lai khó có thể xảy ra trong nhiều môi trường kinh doanh cạnh tranh.
- Bỏ qua các yếu tố chất lượng, chẳng hạn như thay đổi thị hiếu và thời trang.
Gia tốc trình tự
Phương pháp ngoại suy là tạo ra một đường tiếp tuyến ở cuối dữ liệu đã biết và mở rộng nó ra ngoài khu vực này. Giống như phép nội suy, phép ngoại suy sử dụng nhiều phương pháp đòi hỏi kiến thức trước về quy trình tạo ra các điểm dữ liệu hiện có. Phương pháp này bao gồm phép ngoại suy tuyến tính và đa thức, hình nón và phép ngoại suy đường cong Pháp.
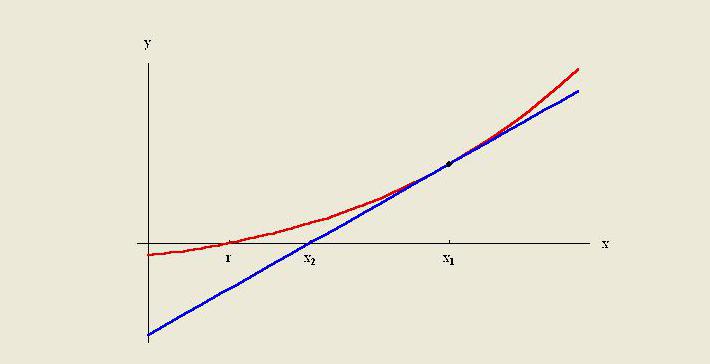
Theo quy định, chất lượng của một phương thức cụ thể bị giới hạn bởi các giả định về chức năng. Trong phân tích số, phép ngoại suy của Richardson là một phương pháp gia tốc trình tự được sử dụng để cải thiện tốc độ hội tụ.Nó được đặt theo tên của Lewis Fry Richardson. Ông đã giới thiệu kỹ thuật tính toán vào đầu thế kỷ 20, tính hữu ích của việc tính toán thực tế khó có thể được đánh giá quá cao.
Các ứng dụng thực tế của phép ngoại suy Richardson bao gồm tích hợp Romberg, áp dụng nó cho quy tắc hình thang và thuật toán Bulliers-Stoehr để giải các phương trình vi phân thông thường.
Phương pháp tuyến tính
Phương pháp ngoại suy tuyến tính rất hữu ích khi một hàm tuyến tính được chỉ định. Điều này được thực hiện bằng cách vẽ một đường tiếp tuyến ở điểm cuối của đồ thị đã cho và mở rộng nó ra xa hơn. Phương pháp ngoại suy này trong dự báo cho kết quả tốt khi điểm được dự đoán không quá xa dữ liệu. Nội suy tuyến tính rất hữu ích trong việc tìm giá trị giữa các điểm đã cho. Nó có thể được coi là "điền vào các khoảng trống" của bảng dữ liệu.
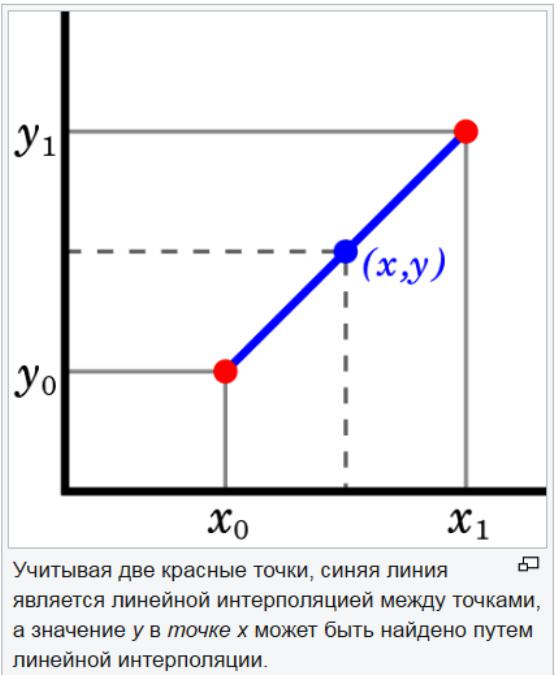
Chiến lược nội suy tuyến tính là sử dụng một đường thẳng để kết nối các điểm đã biết của các giá trị ở hai bên của ẩn số. Nội suy tuyến tính không chính xác cho các tham số phi tuyến tính. Nếu các điểm trong tập dữ liệu thay đổi một lượng lớn, phép nội suy tuyến tính có thể đưa ra ước tính không chính xác.
Phép ngoại suy tuyến tính có thể giúp ước tính các giá trị cao hơn hoặc thấp hơn các giá trị trong tập dữ liệu. Chiến lược của nó là sử dụng một tập hợp con dữ liệu thay vì toàn bộ tập hợp. Đối với loại giá trị này, sẽ hữu ích khi áp dụng phương pháp ngoại suy trong dự báo bằng cách sử dụng hai hoặc ba điểm cuối cùng để ước tính giá trị vượt quá phạm vi dữ liệu.
Phép ngoại suy đa thức và hình nón
Được biết, ba điểm cho một đa thức duy nhất. Một đường cong đa thức có thể được tiếp tục sau khi kết thúc dữ liệu đó. Nó thường được thực hiện bằng phương pháp Newton với sự khác biệt hữu hạn hoặc sử dụng công thức nội suy Lagrange. Một đa thức bậc cao hơn nên được ngoại suy một cách cẩn thận, bởi vì có khả năng xảy ra lỗi với phép ngoại suy đa thức. Nếu điều này xảy ra, ước tính lỗi sẽ tăng theo cấp số nhân với mức độ của đa thức.
Trong toán học, phép ngoại suy đa thức tối thiểu là một phép biến đổi trình tự được sử dụng để tăng tốc độ hội tụ. Mặc dù phương pháp của Aitken được biết đến nhiều nhất, nhưng nó thường thất bại, đặc biệt là đối với các chuỗi vectơ. Trong trường hợp này, một phép lặp được thực hiện để xây dựng ma trận. Cột của nó là sự khác biệt.

Ví dụ, một phương pháp ngoại suy cho một phần hình nón có thể được thực hiện bằng cách sử dụng 5 điểm được chỉ ra ở gần cuối dữ liệu. Trong trường hợp phần hình nón là hình tròn hoặc hình elip, thì nó sẽ lặp lại và tái hợp với chính nó. Parabola hoặc hyperbola không bao giờ giao nhau. Nhưng chúng có thể được uốn cong về trục X. Phép ngoại suy của hình nón có thể được thực hiện trên giấy với một phần hình nón hoặc sử dụng máy tính.
Phương pháp đánh giá toán học
Trong phương pháp ngoại suy này, giá trị cho giai đoạn cơ sở được dự đoán. Các hành động được mô tả dưới đây được hệ thống tự động thực hiện và người dùng không nhìn thấy. Mô tả nhằm tinh chỉnh thuật toán, hiển thị các giá trị dự kiến từ số lượng được lưu trữ trong hệ thống và dự đoán kết quả của phép đo mét.
Phép ngoại suy sử dụng định nghĩa về lượng thủ tục được thực hiện bằng hàm: Yt = f (yi, t, aj).
Để làm cơ sở cho phép ngoại suy, dữ liệu làm tròn của thời kỳ cơ sở điển hình được lưu trữ trong kết quả đọc được thêm vào. Hệ thống xác định trọng số Yt của dữ liệu chuỗi thời gian theo t (thời gian của giai đoạn dự báo) để có được giải pháp chính xác bằng phép ngoại suy. Trong đó tại điểm tham chiếu được lấy yi - cấp của chuỗi và aj - tham số của phương trình xu hướng.
Dự đoán tính năng
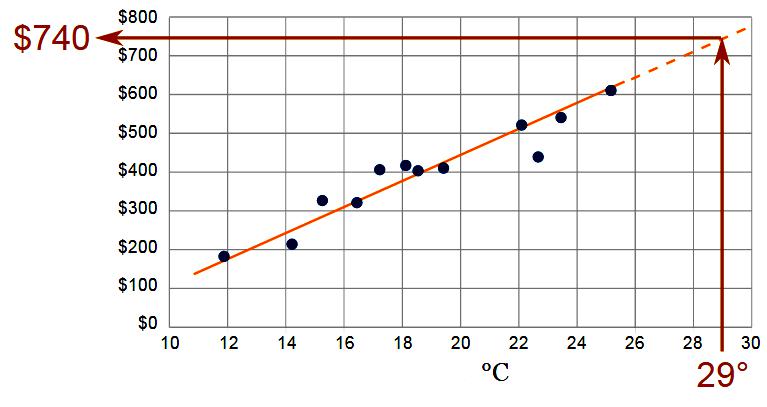
Phương pháp sửa đường cong thống kê được áp dụng để dự đoán chức năng.Các thủ tục thống kê tương ứng với dữ liệu quá khứ của một hoặc nhiều hàm toán học, chẳng hạn như tuyến tính, logarit, Fourier hoặc hàm mũ. Tốt nhất được lựa chọn bởi một bài kiểm tra thống kê. Sau đó, dự báo này được ngoại suy từ kết nối toán học này bằng phương pháp ngoại suy toán học. Một trong những cách dễ nhất để có được ước tính sơ bộ về các điều kiện trong tương lai (hoặc quá khứ) là ngoại suy dữ liệu thay đổi theo thời gian.
Ví dụ, nếu bạn cần đánh giá sơ bộ về mức độ ô nhiễm trong nước uống trong tương lai trước 20 năm, bạn có thể ngoại suy xu hướng này từ 20 năm qua. Điều tương tự cũng được quan sát nếu bạn cần ước tính tỷ lệ hút thuốc hoặc ung thư phổi trong nền trong tương lai. Một dự báo có thể được thực hiện bằng cách tính toán xu hướng trong những năm gần đây. Phép ngoại suy của loại này có thể được thực hiện bằng các phương pháp ít phức tạp hơn. Trong nhiều trường hợp (đặc biệt là trong lĩnh vực tiếp thị và quản lý kinh doanh), phương pháp ngoại suy được sử dụng theo truyền thống, ví dụ, bằng cách xem dữ liệu mới nhất và đánh giá trực quan những gì có nghĩa trong tương lai.
Các phương pháp dựa trên quy tắc cũng có thể được sử dụng bằng cách áp dụng một tập hợp các nguyên tắc hoặc kỳ vọng được xác định trước dựa trên hiểu biết sơ bộ về hệ thống và tính đến dữ liệu mới nhất để diễn giải các sự kiện trong tương lai.
Với bất kỳ phương pháp ngoại suy nào, sự thận trọng rất quan trọng do sự hiện diện của nhiều sự không chắc chắn. Bất kỳ thủ tục ngoại suy nào đều dựa trên giả định rằng thông tin đáng tin cậy có sẵn trong dữ liệu và kiến thức trong quá khứ. Do đó, tương lai được xác định bởi các yếu tố tương tự đã hành động trước đó.
Lỗi dự báo
Sai lầm của phép ngoại suy (chính xác hơn là sai lầm của phép ngoại suy không chính đáng) xảy ra khi hiện tượng chịu trách nhiệm cho một số hiệu ứng cục bộ tầm thường được đọc là hiện tượng toàn cầu lớn. Một lý do khác cho lỗi là đôi khi các quy tắc tổng quát được suy luận từ quá ít sự kiện. Do đó, thuyết tiến hóa của Darwin, là một ví dụ tuyệt vời về việc áp dụng phương pháp ngoại suy, trong đó các cơ chế thay đổi ngẫu nhiên và chọn lọc tự nhiên được công bố có tính đến sự phát triển của các cấu trúc phức tạp như tầm nhìn của động vật có vú hoặc hệ thống miễn dịch của các sinh vật sống.
Khi cố gắng giải thích kết quả nghiên cứu, nhà khoa học nên tránh ngoại suy ngoài phạm vi dữ liệu và nhận thức được các giả định cơ bản để tránh chấp nhận kết luận không hợp lệ. Nói chung, ngoại suy là một công cụ khoa học hợp pháp. Có hai khía cạnh giúp phân biệt giữa phép ngoại suy hợp lệ và sai. Xác suất ngoại suy sai là cao hơn khi các điểm cho dữ liệu không đủ được lấy để xây dựng nó.
Công cụ thống kê Excel
Để tìm mối tương quan giữa năm và kết quả (ví dụ: trong một doanh nghiệp), bạn có thể sử dụng Excel.
Đối với các tác vụ này, các công cụ thống kê để lập mô hình ngoại suy được sử dụng được tích hợp trong tất cả các phiên bản Excel, bắt đầu bằng 97. Quy trình:
- Nhập các giá trị đã biết, ví dụ: tổng doanh số cho năm 2016-2017, nếu bạn cần xác định chúng cho năm 2018 và 2020.
- Phân tích cài đặt, một tính năng yêu cầu sử dụng bổ trợ.
- Để cài đặt nó, hãy trích xuất từ menu "Công cụ", "Tiện ích bổ sung".
- Kiểm tra cửa sổ tiện ích phân tích và xác nhận với.
- Đo lường mối tương quan giữa hai loạt.
- Phép ngoại suy cần được thực hiện chỉ có ý nghĩa nếu có một xu hướng rõ ràng (tương quan) giữa hai bộ số (năm và doanh số) bằng phương pháp ngoại suy.
- Để đo lường mối tương quan này, hãy sử dụng menu "Công cụ", "Tiện ích phân tích".
- Trong danh sách Các công cụ phân tích trong danh sách của bạn
- Trong trường Phạm vi đầu vào, nhập phạm vi được phân tích, ví dụ: A6: B18, Excel sẽ thêm ký hiệu "$".
- Trong khu vực "Tùy chọn đầu ra", kiểm tra phạm vi đầu ra và nhập nó vào trường liền kề.
- Xác nhận với OK.
- Excel tạo một mảng gồm hai hàng trong hai cột. Tìm giá trị tính toán (ví dụ: 0,981). Vì giá trị này gần bằng 1, điều này có nghĩa là có mối tương quan chặt chẽ giữa số năm và số liệu bán hàng. Nếu người dùng nhận được giá trị gần bằng 0, điều này có nghĩa là xu hướng không xảy ra. Trong trường hợp này, phép ngoại suy không có ý nghĩa.
- Một đánh giá các giá trị trong tương lai bắt đầu.
- Chọn phạm vi yêu cầu và nhấp vào nút "Trình hướng dẫn biểu đồ".
- Chọn một biểu đồ (ví dụ: các đám mây điểm) và nhấp vào Kết thúc.
Việc sử dụng trung bình di chuyển
Hai phương pháp ngoại suy này liên quan đến việc sử dụng rộng rãi dữ liệu bán hàng để dự đoán tương lai. Giá trị trung bình di chuyển sẽ lấy một loạt dữ liệu và xóa tan những biến động của họ trong đó. Mục tiêu là để trích xuất dữ liệu cực kỳ theo từng giai đoạn. Đường trung bình thường được tính hàng quý hoặc hàng tuần. Để dự đoán các giá trị trong tương lai, phép ngoại suy liên quan đến việc sử dụng các xu hướng được thiết lập bởi dữ liệu lịch sử. Giả định chính của phép ngoại suy là mẫu sẽ tiếp tục trong tương lai, trừ khi bằng chứng thực tế chỉ ra điều khác. Để hiểu các phương pháp này chi tiết hơn, bạn có thể xem xét một biểu đồ hiển thị doanh số của các tiện ích cho các doanh nghiệp lớn từ năm 2012 đến 2015.
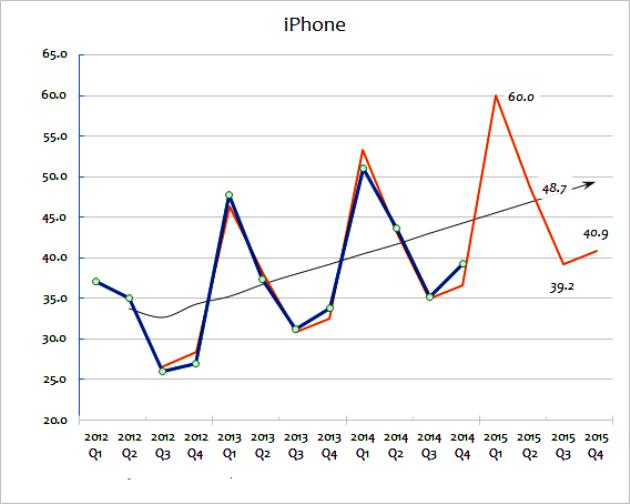
Phương pháp ngoại suy tính toán này cho thấy con số bán hàng thực tế. Như bạn có thể thấy, tổng số lượng bán hàng thay đổi theo từng năm, mặc dù bạn có thể đoán (nhìn vào dữ liệu) rằng có một xu hướng chung cho tăng trưởng doanh số. Đường màu đen hiển thị đường trung bình. Điều này được tính bằng cách thêm các năm bán hàng cuối cùng (ví dụ: Q1 + Q2 + Q3 + Q4) và sau đó chia cho bốn.
Phương pháp này làm trơn tru những thay đổi hàng năm và đưa ra một ý tưởng tốt về xu hướng chung trong doanh số hàng năm. Đường trung bình giúp biểu thị xu hướng tăng trưởng, được biểu thị bằng phần trăm. Chính phép ngoại suy này sẽ được sử dụng đầu tiên để dự đoán con đường bán hàng trong tương lai. Điều này có thể được thực hiện bằng toán học bằng cách sử dụng một bảng tính. Ngoài ra, một xu hướng ngoại suy đơn giản có thể được vẽ trên biểu đồ dưới dạng ước tính sơ bộ.
Tương quan xu hướng
Luôn luôn một công nghệ là tiền thân của người khác. Điều này xảy ra khi những tiến bộ trong công nghệ tiền thân có thể được áp dụng bởi công nghệ theo dõi. Khi các mối quan hệ như vậy tồn tại, kiến thức về những thay đổi trong công nghệ của người tiền nhiệm có thể được sử dụng để dự đoán sự tiến bộ của những người theo dõi công nghệ trong tương lai. Ngoài ra, phép ngoại suy của tiền thân cho phép dự đoán sự tiếp tục của việc theo sau vượt quá thời gian trễ.
Trong trường hợp này, phương pháp ngoại suy các xu hướng được sử dụng, trong đó, ví dụ, các xu hướng về tốc độ của máy bay quân sự và máy bay vận tải được so sánh. Một ví dụ khác về dự báo tương quan xu hướng là dự đoán kích thước và sức mạnh của các máy tính trong tương lai dựa trên những tiến bộ trong công nghệ vi điện tử. Đôi khi công nghệ của những người theo dõi phụ thuộc vào một số công nghệ của tiền thân, nhưng không phụ thuộc vào một người tiền nhiệm.
Các kết hợp cố định của các tiền thân có thể ảnh hưởng đến sự thay đổi trong chuỗi, nhưng thường thì các kết hợp không cố định và các đầu vào của các tiền thân khác nhau về cả kết hợp và cường độ. Ví dụ, sự gia tăng tốc độ máy bay có thể xảy ra do sự cải tiến của động cơ, vật liệu, điều khiển, nhiên liệu, khí động học và sự kết hợp khác nhau của các yếu tố này.
VÍ DỤ tương quan dự báo xu hướng thu được bằng cách ngoại suy: dặm hành khách nói chung, dặm và khả năng hạ cánh trung bình địa lý nói chung.Phép ngoại suy của các xu hướng được xác định theo thống kê cho phép một cách tiếp cận khách quan để dự báo. Tuy nhiên, cách tiếp cận này có những hạn chế và cạm bẫy nghiêm trọng. Bất kỳ lỗi hoặc lựa chọn không chính xác được thực hiện trong việc xác định dữ liệu lịch sử sẽ được phản ánh trong dự báo, làm giảm giá trị của nó.
Ứng dụng, thuộc tính và giới hạn
Phương pháp ngoại suy thuộc về lĩnh vực dự báo. Ông gợi ý rằng các mẫu tồn tại trong quá khứ sẽ tiếp tục trong tương lai và các mẫu này là thường xuyên và có thể đo lường được. Nói cách khác, quá khứ là một chỉ báo tốt về tương lai. Các ứng dụng rất hữu ích để phát triển dữ liệu cơ bản.
Các thuộc tính và giới hạn là các công cụ tính toán đơn giản và rẻ tiền, cũng như các mô hình lý thuyết phức tạp.
- Dữ liệu quá trình - đồ thị và quan sát.
- Điều quan trọng là có một cơ sở dữ liệu tốt và hiểu cấu trúc bên trong nó.
- Kỹ thuật là phù hợp nhất, tỷ lệ và như vậy.
Các thủ tục thống kê tiêu chuẩn tạm thời không dẫn đến lựa chọn chính xác các xu hướng mà người dự báo có thể ngoại suy một cách thoải mái, thực hiện dự báo bằng cách ngoại suy. Trong những trường hợp như vậy, người dự báo có thể điều chỉnh các kết quả thống kê bằng cách sử dụng phán đoán. Nó cũng có thể hoàn toàn bỏ qua số liệu thống kê và ngoại suy toàn bộ xu hướng dựa trên sự đánh giá.
Dự báo được tạo theo cách này ít chính xác hơn dự báo thống kê, nhưng không nhất thiết là không đạt yêu cầu. Một ví dụ về ngoại suy xu hướng chất lượng như vậy là dự đoán độ phức tạp của máy bay. Nỗ lực định lượng xu hướng này đã không thành công. Nhưng tỷ lệ phần trăm có thể di chuyển hoặc điều chỉnh của máy bay đã được ngoại suy với tần suất mà các yếu tố như vậy đã được giới thiệu trong quá khứ. Những dự đoán này khá chính xác.
Thay đổi kỹ thuật cụ thể không thể được dự đoán theo cách này, nhưng mức độ thay đổi có thể. Điều này cung cấp các tài liệu lập kế hoạch hữu ích, chỉ ra một xu hướng trong hành vi trong quá khứ.
