"Stochastic" là một từ mà các nhà vật lý, nhà toán học và các nhà khoa học khác sử dụng để mô tả các quá trình có yếu tố may rủi. Nguồn gốc của nó là Hy Lạp cổ đại. Dịch, nó có nghĩa là "có thể đoán."
Ý nghĩa của từ

"Stochastic" là một khái niệm được sử dụng trong nhiều lĩnh vực khoa học khác nhau. Nó có nghĩa là ngẫu nhiên, ngẫu nhiên, không chắc chắn của một cái gì đó. Trong đạo đức của Aristotle (bức chân dung điêu khắc của ông được trình bày ở trên), khái niệm về stochastic đâm là một định nghĩa đề cập đến khả năng đoán. Rõ ràng, các nhà toán học đã sử dụng nó trên cơ sở rằng yếu tố cơ hội xuất hiện chỉ khi cần thiết để đoán. Từ "stochastic" là một khái niệm được định nghĩa trong Từ điển quốc tế mới là "phỏng đoán".
Vì vậy, có thể lưu ý rằng ý nghĩa kỹ thuật của khái niệm này không chính xác tương ứng với ý nghĩa từ vựng (từ vựng) của nó. Một số tác giả sử dụng biểu thức "quá trình ngẫu nhiên" như một từ đồng nghĩa với thuật ngữ "quá trình ngẫu nhiên".
Tính ngẫu nhiên trong toán học

Việc sử dụng thuật ngữ này trong toán học hiện đang phổ biến. Ví dụ, có một khái niệm như vậy trong lý thuyết xác suất là quá trình ngẫu nhiên. Kết quả của nó không thể được xác định bởi trạng thái ban đầu của hệ thống này.
Việc sử dụng trong toán học của khái niệm "stochasticity" được quy cho các tác phẩm của Vladislav Bortskevich. Chính ông là người đã sử dụng thuật ngữ này với ý nghĩa "đưa ra các giả thuyết." Trong toán học, đặc biệt là trong một phần của khoa học này như lý thuyết xác suất, lĩnh vực nghiên cứu ngẫu nhiên đóng một vai trò quan trọng. Chẳng hạn, có một thứ như ma trận ngẫu nhiên. Các cột hoặc hàng của ma trận này cộng lại thành một.
Toán học ngẫu nhiên (Tài chính)
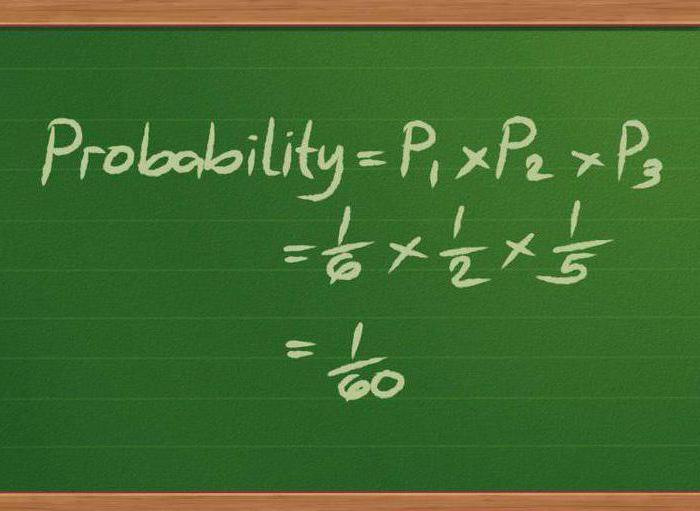
Phần toán học này phân tích các cấu trúc tài chính hoạt động trong điều kiện không chắc chắn. Nó được thiết kế để tìm ra các phương pháp hợp lý nhất để quản lý tài sản và cấu trúc tài chính, có tính đến các yếu tố như tiến hóa ngẫu nhiên, rủi ro, thời gian, v.v.
Trong khoa học, người ta thường phân biệt các cấu trúc và đối tượng sau đây được sử dụng trong toán học tài chính nói chung:
- các công ty (ví dụ, các công ty);
- cá nhân;
- cơ cấu trung gian (quỹ hưu trí, ngân hàng);
- thị trường tài chính.
Đối tượng chính của nghiên cứu toán học tài chính ngẫu nhiên chính xác là cuối cùng của chúng. Phần này dựa trên các chuyên ngành như thống kê các quy trình ngẫu nhiên, lý thuyết về các quy trình ngẫu nhiên, v.v.
Hiện tại, ngay cả những người ở xa khoa học, được biết đến từ nhiều tin tức và ấn phẩm trên các phương tiện truyền thông rằng các giá trị của cái gọi là chỉ số tài chính toàn cầu (ví dụ: chỉ số Dow Jones), giá cổ phiếu đang thay đổi ngẫu nhiên. L. Bachelier đã thực hiện nỗ lực đầu tiên để mô tả bằng toán học sự tiến hóa của giá cổ phiếu. Phương pháp ngẫu nhiên của ông dựa trên lý thuyết xác suất. Luận án của L. Bachelier, trình bày nỗ lực này, đã được xuất bản năm 1900. Các nhà khoa học đã chứng minh công thức hiện được gọi là công thức giá trị hợp lý cho các tùy chọn cuộc gọi. Nó phản ánh xác suất ngẫu nhiên.
Những ý tưởng quan trọng mà sau đó đã dẫn đến sự xuất hiện của một lý thuyết thị trường hiệu quả đã được trình bày trong tác phẩm của M. Kendall, được xuất bản năm 1953. Bài viết này đề cập đến vấn đề động lực giá cổ phiếu. Các nhà nghiên cứu mô tả nó bằng cách sử dụng các quá trình ngẫu nhiên.
Sự ngẫu nhiên trong Vật lý
Cảm ơn các nhà vật lý E. Fermi, S. Ulam, N. Metropolis và D.Neumann được sử dụng rộng rãi phương pháp Monte Carlo. Tên của nó xuất phát từ một sòng bạc nằm trong cùng một thành phố ở một quốc gia như Monaco. Chính tại đây, chú Ulam đã vay tiền cho trò chơi. Sử dụng bản chất của sự lặp lại và cơ hội để nghiên cứu các quy trình tương tự như những gì xảy ra trong một sòng bạc.

Khi áp dụng phương pháp mô hình hóa này, một chất tương tự xác suất được tìm kiếm đầu tiên. Trước đó, mô hình hóa được thực hiện theo hướng ngược lại: nó được sử dụng để xác minh kết quả của vấn đề xác định thu được trước đó. Mặc dù các cách tiếp cận tương tự đã tồn tại trước khi phát hiện ra phương pháp Monte Carlo, nhưng chúng không phổ biến và chung chung.
Enrico Fermi năm 1930 đã áp dụng các kỹ thuật ngẫu nhiên để tính toán các tính chất của neutron, mới được phát hiện vào thời điểm đó. Các phương pháp Monte Carlo sau đó đã được sử dụng khi làm việc trong dự án Manhattan, mặc dù tại thời điểm đó khả năng của máy tính bị hạn chế đáng kể. Vì lý do này, chúng trở nên phổ biến chỉ sau khi máy tính xuất hiện.
Tín hiệu ngẫu nhiên
Tín hiệu thường xuyên và ngẫu nhiên có dạng sóng khác nhau. Nếu chúng ta đo lại cái sau, chúng ta sẽ có các dao động có hình dạng mới, khác với hình trước, nhưng cho thấy sự tương đồng nhất định trong các tính năng thiết yếu. Một ví dụ về tín hiệu ngẫu nhiên là ghi lại dao động sóng biển.
Tại sao cần phải nói về những tín hiệu khá bất thường này? Thực tế là trong nghiên cứu về các hệ thống tự động, chúng thậm chí còn phổ biến hơn dự đoán.
Stochasticity và Artificial Intelligence
Các chương trình trí tuệ nhân tạo ngẫu nhiên làm việc bằng cách sử dụng các phương pháp xác suất. Các thuật toán như tối ưu hóa ngẫu nhiên hoặc mạng thần kinh có thể được trích dẫn làm ví dụ. Điều tương tự cũng áp dụng cho các thuật toán ủ và di truyền mô phỏng. Trong tất cả các trường hợp này, tính ngẫu nhiên có thể được chứa trong vấn đề như vậy hoặc trong kế hoạch một cái gì đó trong điều kiện không chắc chắn. Môi trường xác định cho một tác nhân mô hình hóa đơn giản hơn stochastic.

Vì vậy, như chúng ta thấy, khái niệm quan tâm đến chúng ta được sử dụng trong nhiều lĩnh vực khoa học. Chúng tôi đã liệt kê và chỉ đặc trưng các lĩnh vực chính của ứng dụng của nó. Nghiên cứu của tất cả các quá trình này, bạn thấy, là rất quan trọng và có liên quan. Đó là lý do tại sao khái niệm quan tâm đến chúng ta có thể sẽ được sử dụng trong một thời gian dài trong khoa học.








