Phân tích hồi quy tương quan - Đây là một trong những phương pháp phổ biến nhất để nghiên cứu mối quan hệ giữa các giá trị số. Mục tiêu chính của nó là tìm mối quan hệ giữa hai tham số và mức độ của nó với đạo hàm tiếp theo của phương trình. Ví dụ, chúng tôi có những học sinh đã vượt qua kỳ thi toán và tiếng Anh. Chúng ta có thể sử dụng mối tương quan để xác định xem sự thành công của một thử nghiệm có ảnh hưởng đến kết quả ở một môn học khác hay không. Về phân tích hồi quy, nó giúp dự đoán điểm toán dựa trên số điểm đạt được trong một bài kiểm tra tiếng Anh và ngược lại.

Biểu đồ tương quan là gì?
Bất kỳ phân tích bắt đầu với việc thu thập thông tin. Càng nhiều, kết quả thu được càng chính xác. Trong ví dụ trên, chúng tôi có hai ngành học mà học sinh cần phải vượt qua một kỳ thi. Tỷ lệ thành công của họ là một ước tính. Phân tích tương quan-hồi quy cho thấy liệu kết quả của một môn học có ảnh hưởng đến điểm số trong kỳ thi thứ hai hay không. Để trả lời câu hỏi này, cần phải phân tích xếp hạng của tất cả các sinh viên song song. Nhưng trước tiên bạn cần quyết định biến phụ thuộc. Trong trường hợp này, nó không quá quan trọng. Giả sử một bài kiểm tra toán đã diễn ra trước đó. Điểm trên đó là một biến độc lập (chúng bị hoãn dọc theo abscissa). Tiếng Anh có trong lịch trình sau này. Do đó, ước tính dựa trên nó là một biến phụ thuộc (được vẽ dọc theo tọa độ). Do đó, đồ thị thu được trông giống như một đường thẳng, mối tương quan tuyến tính giữa hai giá trị được chọn càng mạnh. Điều này có nghĩa là học sinh trong toán học có nhiều khả năng có được sự chú ý trong kỳ thi tiếng Anh.
Giả định và đơn giản hóa
Phương pháp phân tích tương quan và hồi quy liên quan đến việc tìm kiếm mối quan hệ nhân quả. Tuy nhiên, ở giai đoạn đầu tiên, bạn cần hiểu rằng những thay đổi ở cả hai đại lượng có thể là do một số thứ ba, chưa được nhà nghiên cứu tính đến. Cũng có thể có mối quan hệ phi tuyến tính giữa các biến, do đó, có được hệ số bằng 0 không phải là kết thúc của thí nghiệm.
Tương quan tuyến tính Pearson
Hệ số này có thể được sử dụng theo hai điều kiện. Giá trị thứ nhất - tất cả các giá trị của các biến là số hữu tỷ, thứ hai - dự kiến các giá trị thay đổi theo tỷ lệ. Hệ số này luôn nằm trong khoảng -1 đến 1. Nếu lớn hơn 0, thì có sự phụ thuộc tỷ lệ thuận trực tiếp, ít hơn - ngược lại, bằng nhau - các giá trị này không ảnh hưởng đến nhau theo bất kỳ cách nào. Khả năng tính toán chỉ số này là cơ sở của phân tích tương quan và hồi quy. Lần đầu tiên, hệ số này được phát triển bởi Karl Pearson dựa trên ý tưởng của Francis Galton.
Thuộc tính và cảnh báo
Hệ số tương quan của Pearson là một công cụ mạnh mẽ, nhưng nó cũng nên được sử dụng một cách thận trọng. Các cảnh báo sau đây được sử dụng:
- Hệ số Pearson chỉ ra sự hiện diện hay vắng mặt của mối quan hệ tuyến tính. Phân tích tương quan-hồi quy không kết thúc ở đó, nó có thể chỉ ra rằng các biến vẫn được liên kết với nhau.
- Người ta phải cẩn thận trong việc giải thích giá trị hệ số. Một mối tương quan có thể được tìm thấy giữa kích thước chân và mức IQ.Nhưng điều này không có nghĩa là một chỉ số xác định cái khác.
- Hệ số Pearson không nói gì về mối quan hệ nhân quả giữa các chỉ số.

Hệ số tương quan xếp hạng của Spearman
Nếu thay đổi giá trị của một chỉ báo dẫn đến tăng hoặc giảm giá trị của một chỉ báo khác, thì điều này có nghĩa là chúng có liên quan. Phân tích hồi quy tương quan, một ví dụ sẽ được đưa ra dưới đây, được kết nối chính xác với các tham số như vậy. Hệ số xếp hạng cho phép bạn đơn giản hóa các tính toán.
Phân tích tương quan và hồi quy: một ví dụ
Giả sử có một đánh giá về hiệu suất của mười doanh nghiệp. Chúng tôi có hai thẩm phán cho họ điểm. Phân tích tương quan và hồi quy của doanh nghiệp trong trường hợp này không thể được thực hiện trên cơ sở hệ số Pearson tuyến tính. Chúng tôi không quan tâm đến mối quan hệ giữa xếp hạng của các thẩm phán. Các cấp bậc của các doanh nghiệp theo thẩm phán là quan trọng.
Loại phân tích này có những ưu điểm sau:
- Hình thức không đối xứng giữa các đại lượng nghiên cứu.
- Dễ sử dụng, bởi vì các cấp bậc có thể được quy cho cả thứ tự tăng dần của giá trị và thứ tự giảm dần.
Yêu cầu duy nhất của loại phân tích này là cần phải chuyển đổi dữ liệu nguồn.
Sự cố ứng dụng
Phân tích tương quan và hồi quy dựa trên các giả định sau:
- Các quan sát được coi là độc lập (một lần mất năm lần của con đại bàng hung không ảnh hưởng đến kết quả của lần lật đồng xu tiếp theo).
- Trong phân tích tương quan, cả hai biến được coi là ngẫu nhiên. Trong hồi quy - chỉ có một (phụ thuộc).
- Khi kiểm tra một giả thuyết, một phân phối bình thường phải được quan sát. Sự thay đổi trong biến phụ thuộc phải giống nhau cho từng giá trị trên abscissa.
- Sơ đồ tương quan chỉ là thử nghiệm đầu tiên của giả thuyết về mối quan hệ giữa hai chuỗi tham số, và không phải là kết quả cuối cùng của phân tích.
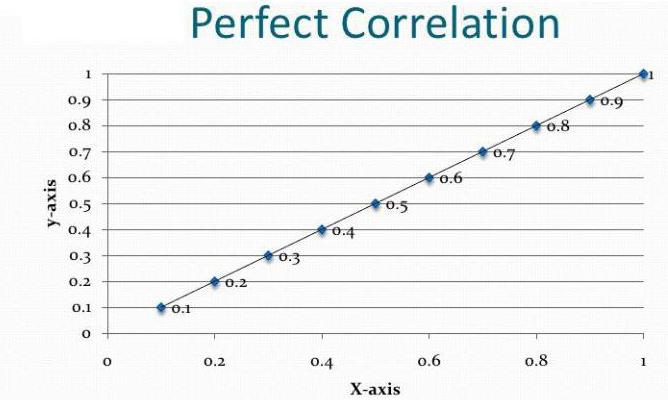
Sự phụ thuộc và nhân quả
Giả sử chúng ta đã tính hệ số tương quan của khối lượng xuất khẩu và GDP. Hóa ra là bằng modulo thống nhất. Chúng ta đã thực hiện phân tích tương quan và hồi quy đến cùng chưa? Tất nhiên là không. Kết quả thu được không có nghĩa là GDP có thể được thể hiện thông qua xuất khẩu. Chúng tôi chưa chứng minh mối quan hệ nhân quả giữa các chỉ số. Phân tích tương quan-hồi quy - dự báo các giá trị của một biến dựa trên biến khác. Tuy nhiên, bạn cần hiểu rằng thường rất nhiều yếu tố ảnh hưởng đến tham số. Xuất khẩu quyết định GDP, nhưng không chỉ nó. Có những yếu tố khác. Ở đây có một mối tương quan và mối quan hệ nhân quả, mặc dù được điều chỉnh cho các thành phần khác của tổng sản phẩm quốc nội.
Một tình huống khác nguy hiểm hơn nhiều. Ở Anh, một cuộc khảo sát đã được thực hiện cho thấy những đứa trẻ có cha mẹ hút thuốc thường là người phạm tội nhiều hơn. Kết luận này dựa trên mối tương quan mạnh mẽ giữa chỉ số. Nhưng anh ấy có đúng không? Thứ nhất, sự phụ thuộc có thể là nghịch đảo. Cha mẹ có thể bắt đầu hút thuốc do căng thẳng từ thực tế là con cái của họ liên tục bị thay đổi và vi phạm pháp luật. Thứ hai, cả hai tham số có thể là do thứ ba. Những gia đình như vậy thuộc về tầng lớp xã hội thấp, được đặc trưng bởi cả hai vấn đề. Do đó, dựa trên mối tương quan, không thể kết luận rằng có mối quan hệ nhân quả.
Tại sao nên sử dụng phân tích hồi quy?
Sự phụ thuộc tương quan liên quan đến việc tìm kiếm mối quan hệ giữa các đại lượng. Mối quan hệ nhân quả trong trường hợp này vẫn còn ở phía sau hậu trường. Các nhiệm vụ của phân tích tương quan và hồi quy chỉ trùng khớp về mặt xác nhận sự tồn tại của mối quan hệ giữa các giá trị của hai đại lượng. Tuy nhiên, ban đầu nhà nghiên cứu không chú ý đến khả năng có mối quan hệ nhân quả. Phân tích hồi quy luôn có hai biến, một trong số đó là phụ thuộc. Nó diễn ra trong một số giai đoạn:
- Chọn đúng mô hình bằng phương pháp bình phương tối thiểu.
- Đạo hàm của một phương trình mô tả ảnh hưởng của một thay đổi trong một biến độc lập trên một biến khác.
Ví dụ, nếu chúng ta nghiên cứu ảnh hưởng của tuổi tác đối với sự tăng trưởng của con người, thì phân tích hồi quy có thể giúp dự đoán những thay đổi qua các năm.
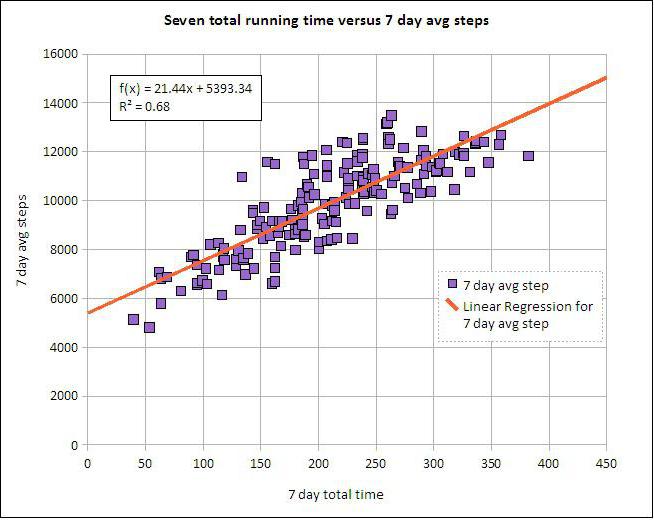
Hồi quy tuyến tính và bội
Giả sử X và Y là hai biến liên quan. Phân tích hồi quy cho phép chúng ta dự đoán độ lớn của một trong số chúng dựa trên các giá trị của cái kia. Ví dụ, trưởng thành và tuổi tác là triệu chứng phụ thuộc. Mối quan hệ giữa chúng được phản ánh bằng hồi quy tuyến tính. Thực tế, bạn có thể diễn đạt X qua Y hoặc ngược lại. Nhưng thường chỉ có một trong các đường hồi quy là chính xác. Sự thành công của phân tích phần lớn phụ thuộc vào việc xác định chính xác biến độc lập. Ví dụ, chúng ta có hai chỉ số: năng suất và lượng mưa. Từ kinh nghiệm hàng ngày, nó trở nên rõ ràng rằng cái đầu tiên phụ thuộc vào cái thứ hai chứ không phải ngược lại.
Hồi quy bội cho phép bạn tính toán một giá trị không xác định dựa trên các giá trị của ba biến trở lên. Ví dụ, năng suất lúa trên một mẫu đất phụ thuộc vào chất lượng hạt, độ phì của đất, phân bón, nhiệt độ và lượng mưa. Tất cả các tham số này ảnh hưởng đến kết quả tổng thể. Để đơn giản hóa mô hình, các giả định sau đây được sử dụng:
- Mối quan hệ giữa các đặc tính độc lập và ảnh hưởng là tuyến tính.
- Đa sắc thái được loại trừ. Điều này có nghĩa là các biến phụ thuộc không được kết nối với nhau.
- Homoskedasticity và tính quy phạm của chuỗi số.
Việc sử dụng phân tích tương quan và hồi quy
Có ba trường hợp chính sử dụng phương pháp này:
- Kiểm tra mối quan hệ ngẫu nhiên giữa số lượng. Trong trường hợp này, nhà nghiên cứu xác định các giá trị của biến và tìm hiểu xem chúng có ảnh hưởng đến sự thay đổi của biến phụ thuộc hay không. Ví dụ, bạn có thể cung cấp cho mọi người liều lượng rượu khác nhau và đo huyết áp của họ. Trong trường hợp này, nhà nghiên cứu biết chắc chắn rằng thứ nhất là nguyên nhân của thứ hai chứ không phải ngược lại. Phân tích tương quan-hồi quy cho phép bạn phát hiện mối quan hệ tuyến tính tỷ lệ thuận trực tiếp giữa hai biến này và rút ra một công thức mô tả nó. Trong trường hợp này, các giá trị được biểu thị bằng các đơn vị đo lường hoàn toàn khác nhau có thể được so sánh.
- Tìm mối quan hệ giữa hai biến mà không mở rộng mối quan hệ nhân quả với chúng. Trong trường hợp này, không có sự khác biệt kích thước mà nhà nghiên cứu gọi là phụ thuộc. Hơn nữa, trong thực tế, có thể cả hai đều bị ảnh hưởng bởi biến thứ ba, do đó chúng thay đổi theo tỷ lệ.
- Tính toán các giá trị của một đại lượng dựa trên số lượng khác. Nó dựa trên một phương trình trong đó các số đã biết được thay thế.
Do đó, phân tích tương quan liên quan đến việc tìm kiếm một kết nối (không phải nguyên nhân) giữa các biến và phân tích hồi quy giải thích nó, thường sử dụng một hàm toán học.








