"Ekstrapolasyon" kelimesi iki basit kelimeden oluşur. Latincede birincisi ekstra sesler ve "dış" için "dış", "anlamına gelir. Aynı Latince ikinci kulağa küfür ve "değişim", "düzeltmek", "pürüzsüz" anlamına gelir. Genel olarak, ekstrapolasyon verilen iki noktanın dışındaki bir değer olarak tanımlanabilir. Amaçlanan sonuca ulaşmak için bilinmeyen bir alandaki verileri genişleten bilinen gerçeklerden neyin elde edildiğinin bir değerlendirme olduğu düşünülmektedir. Bu kavram, şimdiki ve geçmiş eğilimlerin gerçeğini varsayarak geleceğin imajının öngörülmesine de bağlanabilir.
Ekstrapolasyon yöntemi, gelecekteki veri veya gözlemlerin benzer olmaya devam edeceğini varsayar. Böylece, gelecekteki sonuçlar tahmin edilebilir. Matematiksel bir hipotez olarak düşünülebilir. Ekstrapolasyon, belirli bir durumun verilerini ve gerçeklerini kullanır ve sonunda neler olabileceğine dair tahminler sağlar.
Ekstrapolasyon Geçmişi

Bu yöntem genellikle Richardson ekstrapolasyonu veya Romberg metodu olarak adlandırılır. Ancak bu tam olarak doğru değil, çünkü yüzyıllar boyunca bu tür problemleri çözmek için benzer sayısal yöntemler vardı. Bu nedenle, ünlü Richardson h2 (sayısal bir çözüm için ekstrapolasyon) ilk değil. Benzer bir yöntem Huygens hesaplamalarında 1654 gibi erken bir zamanda uygulanmıştır. "Ekstrapolasyon" terimi ilk olarak 1959'da Thomas D. Clareson tarafından bilim ve kurgu kitaplarında yazılmıştır.
Ekstrapolasyon yöntemleri, veri veya işlemlerin uzantısı olarak anlaşılabilir ve bu da benzer bir işlemin bunların dışında uygulanacağını gösterir. Ekstrapolasyon sadece matematikte değil aynı zamanda sosyoloji, psikoloji, tahmin gibi diğer alanlarda da kullanılan önemli bir kavramdır. Örneğin, bir sürücü genellikle vizyonunun dışındaki sürüş koşullarını öngörür. Ekstrapolasyon, veri değerlerinin x1, x2 ..., xn noktaları olarak ele alındığı ve daha sonra değerin verilen bir nokta aralığının sınırına yaklaştığı bir yönteme bağlanabilir.
Kullanımın faydaları:
- Basit bir tahmin yöntemi.
- Çok fazla veri gerekli değil.
- Hızlı ve ucuz analitik.
Bu yöntem istatistiklerde bulunmaktadır. Herhangi bir değer periyodik olarak kaldırılırsa, cevap bir sonraki veri noktasına yaklaşır. Ekstrapolasyon yöntemine bir örnek, verilerin arka planını inceleyen ve geleceğin öngörülen modelini tahmin eden bir hava tahminidir. Daha basit bir örnek, eğer Pazarlar, Pazartesi ve Salı günleri hakkında bilginiz varsa, Çarşamba veya Perşembe günlerini tahmin edebilirsiniz.
Ekstrapolasyon kullanma dezavantajları:
- Güvenilmezlik, tarihsel verilerde önemli dalgalanmalar varsa.
- Geçmişteki trendin gelecekte de devam edeceği varsayımı, pek çok rekabetçi iş ortamında mümkün değildir.
- Tat ve modadaki değişiklikler gibi kalite faktörlerini göz ardı eder.
Sıra ivmesi
Ekstrapolasyon yöntemleri, bilinen verilerin sonunda bir teğet çizgi oluşturmak ve bu alanın ötesine genişletmektir. İnterpolasyon gibi, ekstrapolasyon mevcut veri noktalarını oluşturan işlem hakkında önceden bilgi gerektiren birçok yöntem kullanır. Yöntem, doğrusal ve polinom ekstrapolasyonu, konikler ve Fransız eğrisi ekstrapolasyonunu içerir.
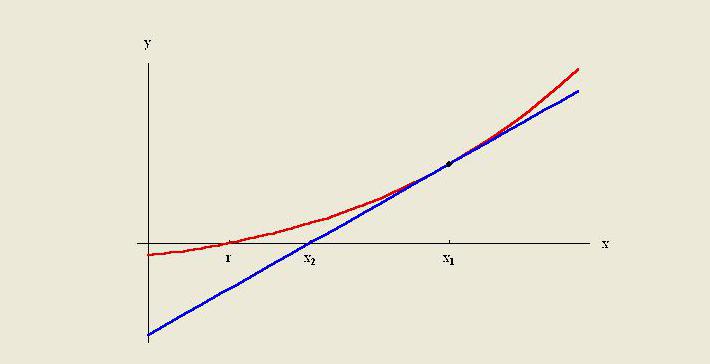
Kural olarak, belirli bir yöntemin kalitesi, işlevle ilgili varsayımlarla sınırlıdır. Sayısal analizde, Richardson ekstrapolasyonu yakınsama hızını arttırmak için kullanılan bir dizi hızlandırma yöntemidir.Lewis Fry Richardson'dan sonra seçildi. Hesaplama tekniğini 20. yüzyılın başında, pratik hesaplamalar için yararlılığı zorlukla tahmin edilemeyecek şekilde tanıttı.
Richardson ekstrapolasyonunun pratik uygulamaları arasında, yamuk kuralına uygulanan Romberg entegrasyonu ve adi diferansiyel denklemleri çözmek için Bulliers-Stoehr algoritması bulunur.
Doğrusal yöntemi
Doğrusal bir değer belirtme yöntemi doğrusal bir işlev belirtildiğinde kullanışlıdır. Bu, belirli bir grafiğin son noktasına teğet bir çizgi çizerek ve ötesine genişleterek yapılır. Tahminlemede bu ekstrapolasyon yöntemi, tahmin edilecek nokta verilerden çok uzak olmadığında iyi sonuçlar verir. Doğrusal enterpolasyon, verilen noktalar arasındaki değerleri bulmakta faydalıdır. Veri tablosunun "boşlukları doldurma" olarak kabul edilebilir.
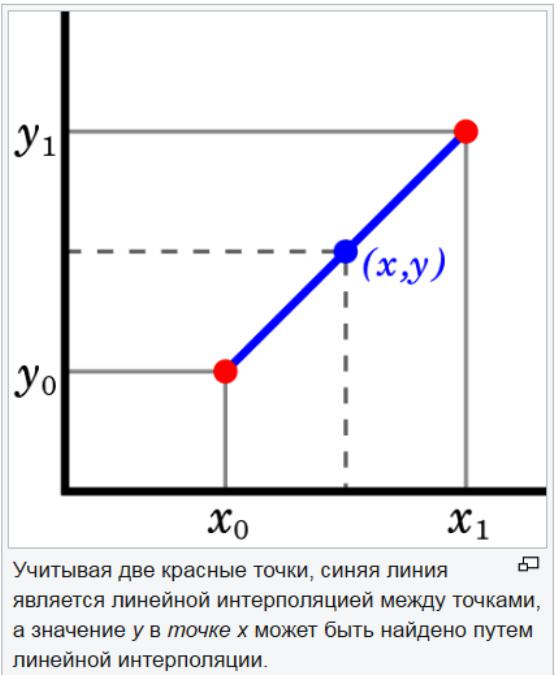
Doğrusal bir enterpolasyon stratejisi, bilinmeyenin her iki tarafındaki bilinen değer noktalarını bağlamak için düz bir çizgi kullanmaktır. Doğrusal enterpolasyon doğrusal olmayan parametreler için doğru değildir. Veri setindeki noktalar büyük miktarda değişirse, doğrusal enterpolasyon yanlış bir tahmin verebilir.
Doğrusal ekstrapolasyon, veri kümesindeki değerlerden daha yüksek veya daha düşük olan değerleri tahmin etmenize yardımcı olabilir. Stratejisi, tüm set yerine veri alt kümesini kullanmaktır. Bu tür bir değer için, veri aralığını aşan bir değeri tahmin etmek için son iki veya üç noktayı kullanarak tahmin etmede ekstrapolasyon yöntemini uygulamak faydalı olacaktır.
Polinom ve konik ekstrapolasyonlar
Üç noktanın benzersiz bir polinom verdiği bilinmektedir. Bu verilerin bitiminden sonra bir polinom eğrisi devam ettirilebilir. Genellikle Newton yöntemi ile sonlu bir farkla veya Lagrange enterpolasyon formülü kullanılarak gerçekleştirilir. Daha yüksek dereceli bir polinom, dikkatli bir şekilde ekstrapolasyona tabi tutulmalıdır, çünkü polinom ekstrapolasyonuyla ilgili ciddi bir hata olasılığı vardır. Bu durumda, hata tahmini polinomun derecesi ile üssel olarak artacaktır.
Matematikte, minimal polinom ekstrapolasyonu, yakınsaklığı hızlandırmak için kullanılan bir dizi dönüşümüdür. Her ne kadar Aitken'in yöntemi en iyi bilinse de, özellikle vektör dizileri için genellikle başarısız olur. Bu durumda, matrisi oluşturan bir yineleme gerçekleştirilir. Sütunları farklılıklardır.

Örneğin, konik bir bölüm için bir ekstrapolasyon yöntemi, verilerin sonuna yakın belirtilen 5 nokta kullanılarak yapılabilir. Konik kısmın bir daire veya elips olması durumunda, geri dönecek ve kendisiyle tekrar birleşecektir. Parabol veya hiperbol asla kesişmez. Fakat X ekseni etrafında geriye doğru bükülebilirler.Konun ekstrapolasyonu, konik bir bölümle veya bir bilgisayar kullanılarak kağıt üzerinde yapılabilir.
Matematiksel Değerlendirme Yöntemi
Bu ekstrapolasyon yönteminde, baz dönemin değeri tahmin edilir. Aşağıda açıklanan eylemler sistem tarafından otomatik olarak gerçekleştirilir ve kullanıcı tarafından görülemez. Tanım, sistemde depolanan miktardan beklenen değerleri gösteren ve sayaç ölçümünün sonucunu tahmin eden algoritmayı geliştirmeyi amaçlamaktadır.
İşlem miktarının tanımını kullanarak ekstrapolasyon işlevi kullanılarak gerçekleştirilir: Yt = f (yi, t, aj).
Ekstrapolasyon için bir temel olarak, okuma sonuçlarında depolanan tipik bir baz dönemin yuvarlatılmış verileri eklenmiştir. Sistem, ekstrapolasyon ile doğru çözümü elde etmek için, zaman serisi verilerinin Yt ağırlığını t (tahmin periyodunun zamanı) olarak belirler. Referans noktasında yi alındığında - seri ve aj düzeyi - trend denkleminin parametresi.
Özellik Tahmini
İstatistiksel bir eğri düzeltme yöntemi, işlevselliği öngörmede uygulanabilir.İstatistiksel işlemler, doğrusal, logaritmik, Fourier veya üstel gibi bir veya daha fazla matematiksel fonksiyonun geçmiş verilerine tekabül eder. En iyisi istatistiksel bir test tarafından seçilir. Sonra bu tahmin, matematiksel ekstrapolasyon yöntemiyle bu matematiksel bağlantıdan tahmin edilir. Gelecekteki (veya geçmişteki) koşulların kaba tahminlerini elde etmenin en kolay yollarından biri, zaman içinde değişen verileri tahmin etmektir.
Örneğin, 20 yıl boyunca içme suyunda gelecekteki kirletici madde seviyelerinin kaba bir değerlendirmesini yapmanız gerekiyorsa, bu eğilimi son 20 yıldan daha fazla tahmin edebilirsiniz. Gelecekte arka planda sigara içmenin veya akciğer kanserinin prevalansını tahmin etmeniz gerektiğinde de aynı şey gözlemlenir. Son yıllarda eğilimleri hesaplayarak bir tahmin yapılabilir. Bu tip ekstrapolasyonlar, daha az karmaşık yöntemler kullanılarak yapılabilir. Çoğu durumda (özellikle pazarlama ve işletme yönetimi alanlarında), ekstrapolasyon yöntemi geleneksel olarak, örneğin en son verileri görüntüleyerek ve gelecekte ne anlama geldiğini sezgisel olarak değerlendirerek kullanılır.
Kural tabanlı yöntemler, sistemin ön anlayışına dayanan bir dizi önceden tanımlanmış ilke veya beklenti uygulayarak ve gelecekteki olayları yorumlamak için en son verileri dikkate alarak da kullanılabilir.
Herhangi bir ekstrapolasyon yönteminde, çok sayıda belirsizliğin varlığından dolayı dikkatli olunması önemlidir. Herhangi bir ekstrapolasyon prosedürü, geçmiş veriler ve bilgilerde güvenilir bilginin mevcut olduğu varsayımına dayanır. Sonuç olarak, gelecek daha önce hareket eden faktörler tarafından belirlenir.
Tahmin hataları
Ekstrapolasyonun yanlışlığı (daha doğrusu, haksız hesaplanan yanlışlığın yanlışlığı), bir dizi önemsiz yerel etkiden sorumlu olan fenomen büyük küresel olaylar olarak okunurken ortaya çıkar. Hatanın bir başka nedeni de, genelleştirilmiş kuralların çok az sayıda gerçeklerden çıkarıldığı yönündedir. Bu nedenle, Darwin’in evrim teorisi, rastgele değişim ve doğal seleksiyon mekanizmalarının, memeli vizyonu veya canlı organizmaların bağışıklık sistemi gibi karmaşık yapıların gelişimini hesaba katacağı ilan edilen ekstrapolasyon yönteminin uygulanmasının harika bir örneğidir.
Araştırma sonuçlarını yorumlamaya çalışırken, bilim insanı, geçersiz sonuçları kabul etmemek için, veri aralığının dışında fazladan tahmin etmekten kaçınmalı ve temel varsayımların farkında olmalıdır. Genel olarak, dış değer bulma meşru bir bilimsel araçtır. Geçerli ve hatalı ekstrapolasyonu ayırt etmeye yardımcı olan iki husus vardır. Hatalı ekstrapolasyon olasılığı, yapımı için yetersiz veriye işaret edildiğinde daha yüksektir.
Excel İstatistik Araçları
Yıllar ve sonuçlar arasında bir ilişki bulmak için (örneğin, bir işletmede) Excel'i kullanabilirsiniz.
Bu görevler için, 97'den itibaren Excel'in tüm sürümlerinde yerleşik olarak ekstrapolasyon modellemesi için istatistiksel araçlar kullanılır.
- 2018 ve 2020 için belirlemeniz gerekiyorsa, örneğin 2016-2017 için toplam satışları bilinen değerleri girin.
- Eklenti kullanımını gerektiren bir özellik olan Analysis Analysis'i yükleyin.
- Yüklemek için, "Araçlar", "Eklentiler" menüsünden çıkartın.
- Analiz programı penceresini kontrol edin ve “OK” ile onaylayın.
- İki seri arasındaki korelasyonu ölçün.
- Yapılması gereken ekstrapolasyon yalnızca, iki sayı kümesi (yıl ve satış) arasında, ekstrapolasyon eğilimleri metodu ile net bir eğilim (korelasyon) varsa anlamlıdır.
- Bu korelasyonu ölçmek için, "Araçlar", "Analiz Yardımcı Programları" menüsünü kullanın.
- “Analiz Araçları” listesinde “Korelasyon Analizi” ni seçin ve “Tamam” ı tıklayın.
- Giriş Aralığı alanına analiz edilen aralığı girin, örneğin A6: B18, Excel "$" sembolünü ekleyecektir.
- "Çıkış Seçenekleri" alanında, çıkış aralığını kontrol edin ve bitişik alana girin.
- OK ile onaylayın.
- Excel, iki sütunda iki satırlık bir dizi oluşturur. Hesaplanan değeri bulun (örneğin, 0.981). Bu değer 1'e yakın olduğu için, yıllar ile satış rakamları arasında güçlü bir ilişki olduğu anlamına gelir. Kullanıcı sıfıra yakın bir değer alırsa, eğilimin oluşmadığı anlamına gelir. Bu durumda, ekstrapolasyon anlamsızdır.
- Gelecekteki değerlerin bir değerlendirmesi başlar.
- İstediğiniz aralığı seçin ve "Grafik Sihirbazı" düğmesini tıklayın.
- Bir grafik seçin (örneğin, bulutlar işaretleyin) ve Son'u tıklayın.
Hareketli ortalamaların kullanımı
Bu iki ekstrapolasyon yöntemi geleceği tahmin etmek için satış verilerinin yaygın şekilde kullanılmasını içerir. Hareketli ortalama değer bir dizi veriyi alır ve içlerindeki dalgalanmaları “düzeltir”. Amaç, verilerin ekstremalarını dönemden döneme çıkarmaktır. Hareketli ortalamalar genellikle üç ayda bir veya haftada bir hesaplanır. Gelecekteki değerleri tahmin etmek için, ekstrapolasyon tarihsel veriler tarafından belirlenen eğilimlerin kullanılmasını içerir. Ekstrapolasyonun ana varsayımı, gerçek kanıt aksini göstermedikçe, numunenin gelecekte devam edeceği şeklindedir. Bu yöntemleri daha ayrıntılı olarak anlamak için, büyük işletmeler için gadgetların satışlarını 2012'den 2015'e kadar gösteren bir tabloyu düşünebilirsiniz.
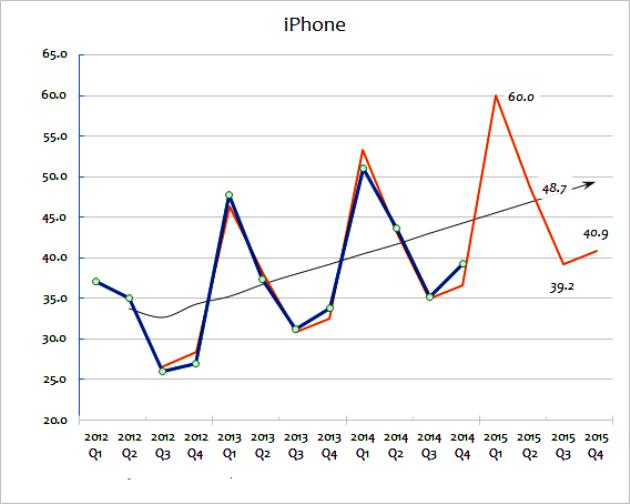
Bu hesaplama ekstrapolasyon yöntemi gerçek satış rakamını gösterir. Görebildiğiniz gibi, toplam satış miktarı yıldan yıla değişmektedir, ancak (verilere bakarak) satışların büyümesi için genel bir eğilim olduğunu tahmin edebilirsiniz. Siyah çizgi hareketli ortalamayı gösterir. Bu, son satış yıllarının eklenmesiyle (örneğin, Q1 + Q2 + Q3 + Q4) ve ardından dörde bölünerek hesaplanır.
Bu yöntem yıllık değişiklikleri yumuşatır ve yıllık satışlardaki genel eğilim hakkında iyi bir fikir verir. Hareketli ortalama, yüzde olarak ifade edilen bir büyüme eğilimini göstermeye yardımcı olur. Gelecekteki satış yolunu tahmin etmek için ilk olarak kullanılacak olan bu ekstrapolasyondur. Bu bir elektronik tablo kullanarak matematiksel olarak yapılabilir. Alternatif olarak, tahmin edilebilir bir eğilim basit bir grafik olarak kaba bir tahmin olarak çizilebilir.
Trend korelasyonu
Her zaman bir teknoloji diğerinin öncüsüdür. Bu, öncül teknolojide kaydedilen ilerlemelerin takipçi teknoloji tarafından benimsenebilmesi durumunda gerçekleşir. Bu tür ilişkiler olduğunda, önceki teknolojilerdeki değişikliklerin bilgisi, teknoloji takipçilerinin gelecekteki ilerlemesini tahmin etmek için kullanılabilir. Ek olarak, öncülün ekstrapolasyonu, takip süresinin gecikme süresinin ötesinde sürmesini öngörmeyi sağlar.
Bu durumda, örneğin askeri ve ulaştırma uçağı hızındaki eğilimlerin karşılaştırıldığı eğilimlerin ekstrapolasyonu yöntemi kullanılır. Trend korelasyonu tahmininin bir başka örneği, mikroelektronik teknolojisindeki gelişmelere dayanarak gelecekteki bilgisayarların boyutunu ve gücünü tahmin etmektir. Bazen takipçilerin teknolojisi, öncekilerden pek çok öncül teknolojiye dayanmaz.
Seleflerin sabit kombinasyonları, sekanstaki değişikliği etkileyebilir, ancak daha sık olarak kombinasyonlar sabit değildir ve seleflerin girdileri hem kombinasyon hem de güç bakımından farklıdır. Örneğin, motorların, malzemelerin, kontrollerin, yakıtın, aerodinamiklerin ve bu faktörlerin çeşitli kombinasyonlarının geliştirilmesinden dolayı uçak hızında bir artış meydana gelebilir.
Ek değer bulma eğilimleriyle elde edilen bir korelasyon tahmini örneği: toplam yolcu mili, toplam coğrafi mil ve ortalama iniş gücü.İstatistiksel olarak belirlenen eğilimlerin ekstrapolasyonu, tahminde objektif bir yaklaşım sağlar. Bununla birlikte, bu yaklaşımın ciddi kısıtlamaları ve tuzakları vardır. Tarihsel verilerin belirlenmesinde yapılan herhangi bir hata veya yanlış seçimler, değerini düşüren tahmine yansıtılacaktır.
Uygulamalar, Nitelikler ve Sınırlamalar
Ekstrapolasyon yöntemi tahmin alanına aittir. Geçmişte var olan kalıpların geleceğe devam edeceğini ve bu kalıpların düzenli olduğunu ve ölçülebileceğini öne sürüyor. Başka bir deyişle, geçmiş geleceğin iyi bir göstergesidir. Uygulamalar, temel verileri geliştirmek için kullanışlıdır.
Nitelikler ve limitler basit ve ucuz hesaplama araçlarının yanı sıra karmaşık teorik modellerdir.
- Proses verileri - grafikler ve gözlemler.
- Anahtar, iyi bir veritabanına sahip olmak ve içindeki yapıyı anlamak.
- Tekniği en uygun, oran vb.
Geçici standart istatistiksel prosedürler, tahmincinin rahatlıkla tahmin edebileceği ve tahminde bulunma yoluyla tahminde bulunabileceği eğilimlerin doğru seçilmesine yol açmaz. Bu gibi durumlarda, tahminci yargılamayı kullanarak istatistiksel sonuçları “ayarlayabilir”. Ayrıca istatistikleri tamamen görmezden gelebilir ve tüm eğilimi karara dayalı olarak tahmin edebilir.
Bu şekilde oluşturulan tahminler istatistiksel tahminlerden daha az doğrudur, ancak zorunlu olarak tatmin edici değildir. Kalite trendinin böyle bir ekstrapolasyonuna bir örnek, uçak karmaşıklığını tahmin etmektir. Bu eğilimi ölçmeye çalışmak başarılı olmamıştır. Ancak uçağın hareketli veya ayarlanabilir parçalarının yüzdesi, bu elemanların geçmişte tanıtılma sıklığıyla tahmin edildi. Bu tahminler oldukça doğruydu.
Belirli teknik değişiklikler bu şekilde tahmin edilemez, ancak değişimin derecesi olabilir. Bu, geçmiş davranışlarda bir eğilim olduğunu gösteren faydalı planlama materyalleri sağlar.
