Ang tambalang salitang "extrapolation" ay binubuo ng dalawang simpleng salita. Ang una sa Latin ay tunog nang labis at nangangahulugang "labas", "para sa", "sa labas". Ang pangalawa sa parehong wikang Latin ay tunog ng polire at nangangahulugang "baguhin", "ituwid", "makinis". Sa pangkalahatan, ang extrapolation ay maaaring tukuyin bilang isang halaga sa labas ng dalawang naibigay na puntos. Itinuturing na isang pagtatasa kung ano ang nakuha mula sa mga kilalang katotohanan na nagpapalawak ng data sa isang hindi kilalang lugar upang makarating sa nais na resulta. Ang konsepto na ito ay maaari ring maiugnay sa hula ng imahe ng hinaharap, sa pag-aakma ng katotohanan ng kasalukuyan at mga nakaraang uso.
Ipinapalagay ng pamamaraang extrapoloh na ang data o mga obserbasyon sa hinaharap ay magpapatuloy na magkatulad. Kaya, ang mga resulta sa hinaharap ay maaaring mahulaan. Maaari itong isaalang-alang bilang isang hypothesis ng matematika. Ginagamit ng Extrapolation ang data at mga katotohanan ng isang tiyak na sitwasyon at nagbibigay ng mga hula tungkol sa kung ano ang maaaring mangyari sa katapusan.
Kasaysayan ng Extrapolusyon

Ang pamamaraang ito ay madalas na tinutukoy bilang extrapolasyon ng Richardson o ang paraan ng Romberg. Ngunit hindi ito ganap na tama, dahil sa maraming siglo ay magkatulad na mga pamamaraan ng numero para sa paglutas ng mga nasabing problema. Samakatuwid, ang sikat na Richardson h2 (extrapolation para sa isang numerical solution) ay hindi ang una. Ang isang katulad na pamamaraan ay naaangkop sa mga kalkulasyon ng Huygens nang maaga ng 1654. Ang salitang "extrapolation" mismo ay unang naisaon ni Thomas D. Clareson noong 1959 sa isang libro sa science at fiction.
Ang mga pamamaraan ng Extrapolation ay maaaring maunawaan bilang pagpapalawak ng data o mga proseso, na nagmumungkahi na ang isang katulad na proseso ay ilalapat sa labas ng mga ito. Ang Extrapolation ay isang mahalagang konsepto na ginamit hindi lamang sa matematika, kundi pati na rin sa iba pang mga lugar, tulad ng sosyolohiya, sikolohiya, pagtataya. Halimbawa, ang isang driver ay karaniwang extrapolates na mga kondisyon sa pagmamaneho sa labas ng kanyang paningin. Ang pagpapahaba ay maaaring maiugnay sa isang pamamaraan kung saan ang mga halaga ng data ay isinasaalang-alang bilang mga puntos na x1, x2 ..., xn, at pagkatapos ay ang halaga ay lapitan ang limitasyon ng isang naibigay na hanay ng mga puntos.
Mga pakinabang ng paggamit:
- Isang simpleng pamamaraan ng pagtataya.
- Hindi gaanong data ang kinakailangan.
- Mabilis at murang analytics.
Ang pamamaraan ay umiiral sa mga istatistika. Kung ang anumang mga halaga ay pana-panahong tinanggal, ang sagot ay lalapit sa susunod na punto ng data. Ang isang halimbawa ng isang paraan ng extrapilation ay isang forecast ng panahon, na isinasaalang-alang ang kasaysayan ng data at extrapolates isang hinulaang modelo ng hinaharap. Isang mas simpleng halimbawa, kung mayroon kang impormasyon tungkol sa Linggo, Lunes at Martes, maaari mong i-extrapolate ang Miyerkules o Huwebes.
Mga kawalan ng paggamit ng extrapolation:
- Hindi pagkatiwalaan, kung may mga makabuluhang pagbabago sa makasaysayang data.
- Ang palagay na ang nakaraang takbo ay magpapatuloy sa hinaharap ay halos hindi posible sa maraming mga mapagkumpitensyang kapaligiran sa negosyo.
- Hindi pansinin ang mga kalidad na kadahilanan, tulad ng mga pagbabago sa mga panlasa at fashion.
Pagkabilis ng pagkakasunud-sunod
Ang mga pamamaraan ng extrapolation ay upang lumikha ng isang padaplis na linya sa dulo ng kilalang data at palawakin ito lampas sa lugar na ito. Tulad ng interpulasyon, ang extrapolation ay gumagamit ng maraming mga pamamaraan na nangangailangan ng paunang kaalaman sa proseso na lumilikha ng umiiral na mga puntos ng data. Kasama sa pamamaraang ito ang linear at polynomial extrapolation, conics at French curve extrapolation.
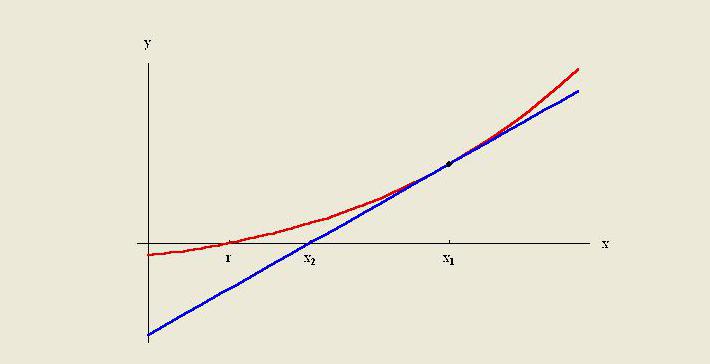
Bilang isang patakaran, ang kalidad ng isang partikular na pamamaraan ay limitado sa pamamagitan ng pagpapalagay tungkol sa pag-andar. Sa pagtatasa ng de-numerong, ang extronolasyon ng Richardson ay isang pamamaraan ng pagkabilis ng pagkakasunod-sunod na ginamit upang mapabuti ang rate ng tagpo.Ito ay pinangalanan sa pamamagitan ng Lewis Fry Richardson. Ipinakilala niya ang pamamaraan sa pagkalkula sa simula ng ika-20 siglo, ang pagiging kapaki-pakinabang ng kung saan para sa mga praktikal na pagkalkula ay maaaring hindi masobrahan.
Ang mga praktikal na aplikasyon ng extrapolasyon ng Richardson ay kasama ang pagsasama ng Romberg, na nalalapat ito sa panuntunan ng trapezoid at ang algorithm ng Bulliers-Stoehr upang malutas ang mga ordinaryong equation na kaugalian.
Paraan ng guhit
Ang paraan ng pagpapahaba ng linear ay kapaki-pakinabang kapag ang isang linear function ay tinukoy. Ginagawa ito sa pamamagitan ng pagguhit ng isang linya ng tangent sa dulo ng isang naibigay na graph at palawakin ito nang higit pa. Ang pamamaraang ito ng extrapolation sa pagtataya ay nagbibigay ng magagandang resulta kapag ang point na mahulaan ay hindi masyadong malayo sa data. Ang linear na paghihiwalay ay kapaki-pakinabang sa paghahanap ng mga halaga sa pagitan ng mga ibinigay na puntos. Maaari itong isaalang-alang bilang "pagpuno sa mga gaps" ng talahanayan ng data.
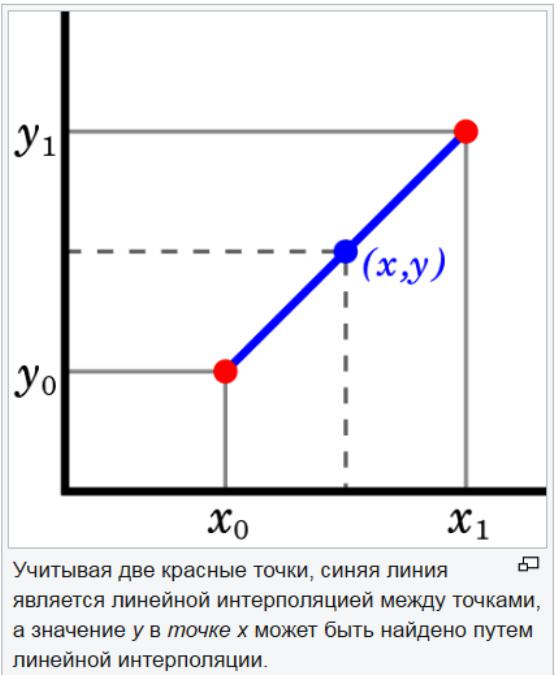
Ang isang guhit na diskarte sa paghihiwalay ay gumamit ng isang tuwid na linya upang ikonekta ang mga kilalang puntos ng mga halaga sa magkabilang panig ng hindi kilalang. Ang linear na paghihiwalay ay hindi tumpak para sa mga non-linear na mga parameter. Kung ang mga puntos sa data set ay nagbabago sa pamamagitan ng isang malaking halaga, ang magkahiwalay na paghihiwalay ay maaaring magbigay ng hindi tamang pagtatantya.
Ang linear extrapolation ay makakatulong sa pagtantya ng mga halaga na mas mataas o mas mababa kaysa sa mga halaga sa set ng data. Ang diskarte nito ay ang paggamit ng isang subset ng data sa halip ng buong hanay. Para sa ganitong uri ng halaga, kapaki-pakinabang na mag-aplay ang paraan ng extrapolation sa pagtataya gamit ang huling dalawa o tatlong puntos upang matantya ang isang halaga na lumampas sa saklaw ng data.
Polynomial at conical extrapolations
Ito ay kilala na ang tatlong puntos ay nagbibigay ng isang natatanging polynomial. Ang isang kurbatang polynomial ay maaaring magpatuloy pagkatapos ng pagtatapos ng naturang data. Karaniwan itong isinasagawa ng pamamaraang Newton na may isang may hangganang pagkakaiba o gamit ang Lagrange interporning formula. Ang isang mas mataas na order na polynomial ay dapat na extrapolated na may nararapat na pag-aalaga, dahil mayroong isang makatarungang pagkakataon ng pagkakamali sa polynomial extrapolation. Kung nangyari ito, ang pagtatantya ng error ay tataas nang malaki sa antas ng polynomial.
Sa matematika, ang minimal na polynomial extrapolation ay isang pagkakasunud-sunod na pagbabagong ginamit upang mapabilis ang kombinasyon. Bagaman ang pamamaraan ni Aitken ay pinakamahusay na kilala, madalas itong nabigo, lalo na para sa mga pagkakasunud-sunod ng vector. Sa kasong ito, ang isang pag-ulit ay isinasagawa na bumubuo sa matris. Ang mga haligi nito ay mga pagkakaiba-iba.

Halimbawa, ang isang paraan ng extrapilation para sa isang seksyong conical ay maaaring gawin gamit ang 5 puntos na ipinahiwatig malapit sa dulo ng data. Kung sakaling ang seksyon ng conical ay isang bilog o isang ellipse, pagkatapos ay i-loop ito muli at muling pagsasama. Ang Parabola o hyperbola ay hindi kailanman bumalandra. Ngunit maaari silang baluktot pabalik tungkol sa X axis.Ang pag-extrap ng kono ay maaaring gawin sa papel na may isang seksyong conical o gamit ang isang computer.
Paraan ng Pagsusuri sa matematika
Sa pamamaraang ito ng ekstrapolasyon, ang halaga para sa panahon ng base ay hinuhulaan. Ang mga pagkilos na inilarawan sa ibaba ay awtomatikong ginanap ng system at hindi nakikita ng gumagamit. Ang paglalarawan ay inilaan upang pinuhin ang algorithm, na ipinapakita ang mga inaasahang halaga mula sa halagang nakaimbak sa system, at hinuhulaan ang resulta ng pagsukat ng metro.
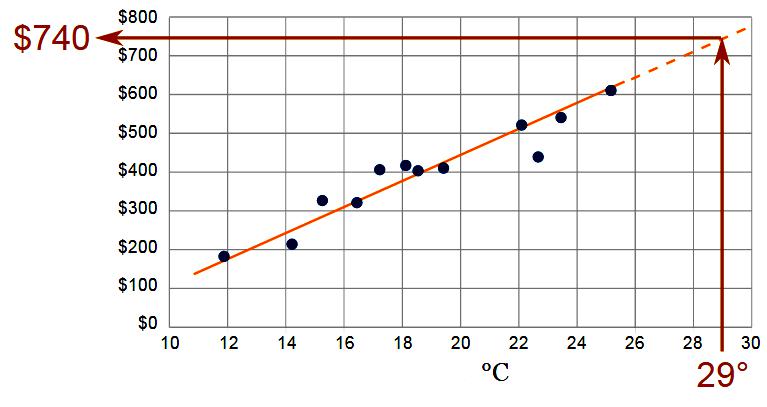
Ang pagpapahaba gamit ang kahulugan ng dami ng pamamaraan ay isinasagawa gamit ang pagpapaandar: Yt = f (yi, t, aj).
Bilang isang batayan para sa pagpapahaba, ang bilog na data ng isang tipikal na tagal ng base na nakaimbak sa mga resulta ng pagbasa ay idinagdag. Tinutukoy ng system ang bigat Yt ng data ng serye ng oras sa t (oras ng panahon ng pagtataya) upang makuha ang tamang solusyon sa pamamagitan ng extrapolation. Kung saan sa sanggunian point ay kinuha yi - ang antas ng serye at aj - ang parameter ng equation ng trend.
Tampok na Prediksyon
Ang pamamaraan ng pag-aayos ng curve ng statistical ay naaangkop sa paghuhula ng pag-andar.Ang mga pamamaraan ng istatistika ay tumutugma sa nakaraang data ng isa o higit pang mga pag-andar sa matematika, tulad ng linear, logarithmic, Fourier, o exponential. Ang pinakamahusay na ay pinili ng isang statistical test. Pagkatapos ang forecast na ito ay extrapolated mula sa koneksyon sa matematika na ito sa pamamagitan ng pamamaraan ng matematika extrapolation. Ang isa sa mga pinakamadaling paraan upang makakuha ng magaspang na mga pagtatantya sa mga kondisyon sa hinaharap (o nakaraan) ay ang extrapolate data na nagbabago sa paglipas ng panahon.
Halimbawa, kung kailangan mong gumawa ng isang magaspang na pagtatasa sa mga antas ng hinaharap ng mga pollutant sa pag-inom ng tubig sa loob ng 20 taon nang maaga, maaari mong i-extrapolate ang trend na ito mula sa huling 20 taon. Ang parehong ay sinusunod kung kailangan mong matantya ang paglaganap ng paninigarilyo o kanser sa baga sa background sa hinaharap. Ang isang forecast ay maaaring gawin sa pamamagitan ng pagkalkula ng mga uso sa mga nakaraang taon. Ang mga Extrapolations ng ganitong uri ay maaaring gawin gamit ang hindi gaanong kumplikadong pamamaraan. Sa maraming mga kaso (lalo na sa mga lugar ng pamamahala at pamamahala ng negosyo), ang pamamaraan ng ekstrapolasyon ay tradisyonal na ginagamit, halimbawa, sa pamamagitan ng pagtingin sa pinakabagong data at intuitively na pagsusuri kung ano ang ibig sabihin sa hinaharap.
Ang mga pamamaraan na nakabatay sa panuntunan ay maaari ding magamit sa pamamagitan ng paglalapat ng isang hanay ng mga paunang natukoy na mga prinsipyo o inaasahan batay sa isang paunang pag-unawa sa system at isinasaalang-alang ang pinakabagong data upang bigyang kahulugan ang mga kaganapan sa hinaharap.
Sa anumang paraan ng extrapolation, mahalaga ang pag-iingat dahil sa pagkakaroon ng maraming mga kawalan ng katiyakan. Ang anumang pamamaraan ng extrapolation ay batay sa pag-aakalang ang maaasahang impormasyon ay magagamit sa nakaraang data at kaalaman. Dahil dito, ang hinaharap ay natutukoy ng parehong mga kadahilanan na kumilos dati.
Pagtataya ng Mga Mali
Ang pagkahulog ng extrapolation (mas tiyak, ang pagkahulog ng hindi patas na pag-extrapolate) ay nangyayari kapag ang kababalaghan na responsable para sa isang bilang ng mga walang kabuluhan na lokal na epekto ay nabasa bilang mahusay na pandaigdigang mga kababalaghan. Ang isa pang kadahilanan para sa pagkakamali ay kung minsan ang mga pangkalahatang tuntunin ay binabawas mula sa napakakaunting mga katotohanan. Kaya, ang teorya ng ebolusyon ni Darwin ay isang kamangha-manghang halimbawa ng paglalapat ng paraan ng extrapolation, kung saan ang mga mekanismo ng mga random na pagbabago at likas na pagpili ay inihayag na isinasaalang-alang ang pag-unlad ng mga kumplikadong istruktura na tulad ng mammalian vision o immune system ng mga nabubuhay na organismo.
Kapag sinusubukan na bigyang-kahulugan ang mga resulta ng pananaliksik, dapat na iwasan ng siyentipiko ang labis na pagkalabas sa labas ng saklaw ng data at magkaroon ng kamalayan ng mga pinagbabatayan na pagpapalagay upang maiwasan ang pagtanggap ng hindi wastong mga konklusyon. Sa pangkalahatan, ang extrapolation ay isang lehitimong tool na pang-agham. Mayroong dalawang mga aspeto na makakatulong na makilala sa pagitan ng wasto at maling pagsasabog. Ang posibilidad ng maling pagkakamali ay mas mataas kapag ang mga puntos para sa hindi sapat na data ay nakuha para sa pagtatayo nito.
Mga tool sa Excel Statistical
Upang makahanap ng isang ugnayan sa pagitan ng mga taon at mga resulta (halimbawa, sa isang negosyo), maaari mong gamitin ang Excel.
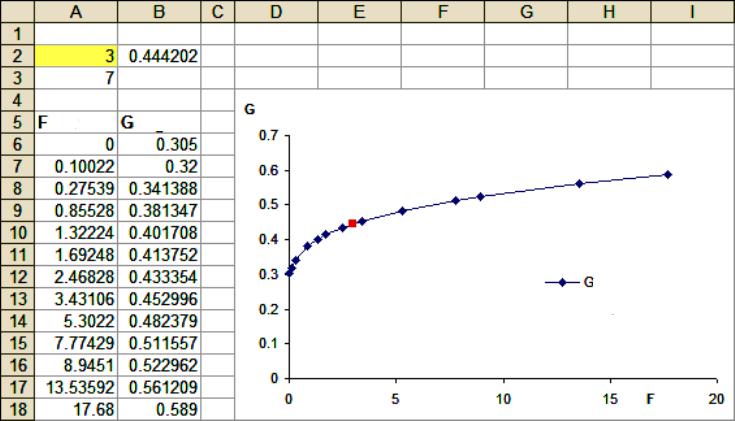
Para sa mga gawaing ito, ginagamit ang mga tool sa istatistika para sa pagmomolde ng extrapolation na binuo sa lahat ng mga bersyon ng Excel, na nagsisimula sa 97. Pamamaraan:
- Ipasok ang mga kilalang halaga, halimbawa, kabuuang mga benta para sa 2016-2017, kung kailangan mong matukoy ang mga ito para sa 2018 at 2020.
- I-install ang Pagsusuri, isang tampok na nangangailangan ng paggamit ng isang add-in.
- Upang mai-install ito, kunin mula sa menu na "Mga tool", "Add-ons".
- Suriin ang window window ng pagsusuri at kumpirmahin sa "OK".
- Sukatin ang mga ugnayan sa pagitan ng dalawang serye.
- Ang extrapolation na kailangang gawin ay may katuturan lamang kung mayroong malinaw na takbo (ugnayan) sa pagitan ng dalawang hanay ng mga numero (taon at benta) sa pamamagitan ng pamamaraan ng mga extrapolating na mga uso.
- Upang masukat ang ugnayan na ito, gamitin ang menu na "Mga tool", "Mga Utility sa Pagtatasa".
- Sa listahan ng "Mga tool sa Pagsusuri" piliin ang "Pagsusuri ng Korelasyon" at i-click ang "OK".
- Sa patlang ng Input Range ipasok ang nasuri na saklaw, halimbawa A6: B18, idaragdag ni Excel ang simbolo na "$".
- Sa lugar na "Output Opsyon", suriin ang saklaw ng output at ipasok ito sa katabing patlang.
- Kumpirma sa OK.
- Lumilikha ang Excel ng isang hanay ng dalawang mga hilera sa dalawang mga haligi. Hanapin ang kinakalkula na halaga (halimbawa, 0.981). Dahil ang halagang ito ay malapit sa 1, nangangahulugan ito na mayroong isang malakas na ugnayan sa pagitan ng mga taon at mga numero ng benta. Kung natatanggap ng gumagamit ang isang halaga na malapit sa zero, nangangahulugan ito na hindi nangyayari ang takbo. Sa kasong ito, ang extrapolation ay hindi magkaroon ng kahulugan.
- Ang pagsusuri ng mga halagang hinaharap ay nagsisimula.
- Piliin ang kinakailangang saklaw at i-click ang pindutan ng "Chart Wizard".
- Pumili ng isang tsart (halimbawa, point ulap) at i-click ang Tapos na.
Ang paggamit ng mga average na gumagalaw
Ang dalawang pamamaraang extrapilation na ito ay nagsasangkot ng malawakang paggamit ng data ng mga benta upang mahulaan ang hinaharap. Ang gumagalaw na average na halaga ay tumatagal ng isang serye ng data at "kininis" ang mga pagbabago sa kanila. Ang layunin ay upang kunin ang extrema ng data sa bawat oras. Ang paglipat ng mga average ay madalas na kinakalkula quarterly o lingguhan. Upang mahulaan ang mga hinaharap na halaga, ang extrapolasyon ay nagsasangkot sa paggamit ng mga trend na itinatag ng makasaysayang data. Ang pangunahing pag-aakala ng extrapolation ay ang sampol ay magpapatuloy sa hinaharap, maliban kung ang aktwal na katibayan ay nagpapahiwatig kung hindi man. Upang maunawaan ang mga pamamaraang ito nang mas detalyado, maaari mong isaalang-alang ang isang tsart na nagpapakita ng mga benta ng mga gadget para sa mga malalaking negosyo mula 2012 hanggang 2015.
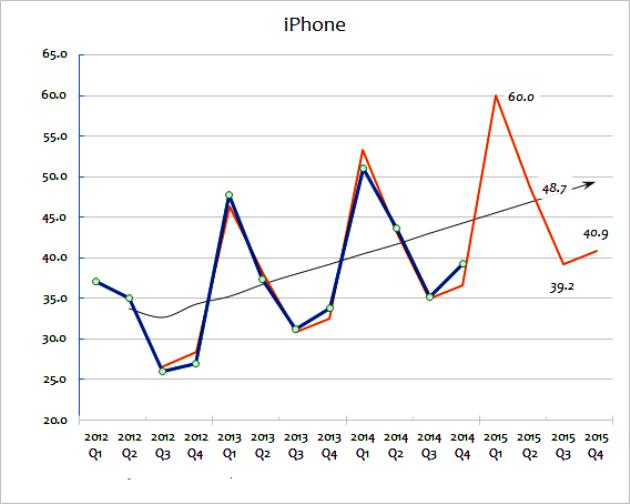
Ang pamamaraang extrapolate ng pagkalkula na ito ay nagpapakita ng aktwal na figure ng benta. Tulad ng nakikita mo, ang kabuuang halaga ng mga benta ay nag-iiba mula sa taon hanggang taon, kahit na maaari mong hulaan (pagtingin sa data) na mayroong isang pangkalahatang kalakaran para sa paglago ng mga benta. Ipinapakita ng itim na linya ang paglipat average. Ito ay kinakalkula sa pamamagitan ng pagdaragdag ng mga huling taon ng pagbebenta (hal. Q1 + Q2 + Q3 + Q4) at pagkatapos ay paghatiin ng apat.
Ang pamamaraang ito ay naglalabas ng taunang mga pagbabago at nagbibigay ng isang magandang ideya ng pangkalahatang kalakaran sa taunang mga benta. Ang isang average na paglipat ay tumutulong upang magpahiwatig ng isang kalakaran sa paglago, na ipinahayag bilang isang porsyento. Ito ang extrapolation na gagamitin muna upang mahulaan ang landas ng mga benta sa hinaharap. Magagawa ito sa matematika gamit ang isang spreadsheet. Bilang kahalili, ang isang extrapolated na takbo ay maaaring iguguhit lamang sa isang tsart bilang isang magaspang na pagtatantya.
Pag-ugnay ng uso
Laging isang teknolohiya ang nangunguna sa isa pa. Nangyayari ito kapag ang mga pagsulong na ginawa sa teknolohiyang pang-uumpisa ay maaaring gamitin ng teknolohiyang tagasunod. Kapag umiiral ang gayong mga ugnayan, ang kaalaman sa mga pagbabago sa teknolohiya ng mga nauna ay maaaring magamit upang mahulaan ang pag-unlad ng mga tagasunod ng teknolohiya sa hinaharap. Bilang karagdagan, pinapayagan ka ng extrapolation ng precursor na mahulaan ang pagpapatuloy ng sundin na lampas sa pagkaantala sa oras.
Sa kasong ito, ang paraan ng extrapolation ng mga uso ay ginagamit, kung saan, halimbawa, ang mga uso sa bilis ng militar at sasakyang panghimpapawid ay inihambing. Ang isa pang halimbawa ng pagtataya ng ugnayan sa takbo ay hinuhulaan ang laki at kapangyarihan ng mga hinaharap na computer batay sa pagsulong sa teknolohiya ng microelectronic. Minsan ang teknolohiya ng mga tagasunod ay nakasalalay sa maraming mga teknolohiya ng mga nauna, ngunit hindi sa isang nauna.
Ang mga nakapirming kumbinasyon ng mga nauna ay maaaring makaapekto sa pagbabago sa pagkakasunud-sunod, ngunit mas madalas ang mga kumbinasyon ay hindi naayos, at ang mga input ng mga nauna ay magkakaiba sa parehong kumbinasyon at lakas. Halimbawa, ang pagtaas ng bilis ng sasakyang panghimpapawid ay maaaring mangyari dahil sa pagpapabuti ng mga makina, materyales, kontrol, gasolina, aerodynamics at iba't ibang mga kumbinasyon ng mga kadahilanang ito.
Isang halimbawa ng isang pagtataya ng ugnayan na nakuha ng mga trend ng extrapolating: kabuuang milya ng pasahero, kabuuang mga geograpikal na milya, at average na kapangyarihan ng landing.Ang pagpapahaba ng mga istatistika na tinukoy ng istatistika ay nagbibigay-daan sa isang layunin na diskarte sa pagtataya. Gayunpaman, ang pamamaraang ito ay may malubhang mga limitasyon at mga pitfalls. Ang anumang mga pagkakamali o maling mga pagpipilian na ginawa sa pagpapasiya ng makasaysayang data ay makikita sa forecast, na binabawasan ang halaga nito.
Mga Aplikasyon, Mga Katangian at Limitasyon
Ang pamamaraan ng ekstrapolasyon ay nabibilang sa larangan ng pagtataya. Iminumungkahi niya na ang mga pattern na umiiral noong nakaraan ay magpapatuloy sa hinaharap, at na ang mga pattern na ito ay regular at maaaring masukat. Sa madaling salita, ang nakaraan ay isang mahusay na tagapagpahiwatig ng hinaharap. Ang mga aplikasyon ay kapaki-pakinabang para sa pagbuo ng data ng baseline.
Ang mga katangian at limitasyon ay simple at murang mga tool sa pagkalkula, pati na rin ang mga kumplikadong teoretikal na modelo.
- Data ng proseso - mga graph at mga obserbasyon.
- Ang susi ay ang pagkakaroon ng isang mahusay na database at pag-unawa sa istraktura sa loob nito.
- Ang pamamaraan ay ang pinakamahusay na akma, ratio at iba pa.
Ang pansamantalang pamantayang pamamaraan ng istatistika ay hindi humahantong sa tumpak na pagpili ng mga uso na maaaring ihabol ng forecaster nang may ginhawa, na isinasagawa ang forecast sa pamamagitan ng extrapolation. Sa mga nasabing kaso, ang forecaster ay maaaring "ayusin" ang mga resulta ng istatistika gamit ang paghatol. Maaari rin itong ganap na huwag pansinin ang mga istatistika at i-extrapolate ang buong takbo batay sa paghatol.
Ang mga pagtataya na nabuo sa ganitong paraan ay hindi gaanong tumpak kaysa sa mga istatistikong pagtataya, ngunit hindi kinakailangan na hindi kasiya-siya. Isang halimbawa ng tulad ng isang extrapolate ng isang kalidad na takbo ay ang paghuhula ng pagiging kumplikado ng sasakyang panghimpapawid. Ang mga pagsisikap upang matukoy ang kalakaran na ito ay hindi naging matagumpay. Ngunit ang porsyento ng naailipat o nababagay na mga bahagi ng sasakyang panghimpapawid ay extrapolated na may dalas na kung saan ang mga naturang elemento ay ipinakilala sa nakaraan. Ang mga pagtataya na ito ay medyo tumpak.
Ang mga tukoy na pagbabago sa teknikal ay hindi maaaring mahulaan sa ganitong paraan, ngunit ang antas ng pagbabago ay maaaring. Nagbibigay ito ng mga kapaki-pakinabang na materyales sa pagpaplano, na nagpapahiwatig ng isang kalakaran sa nakaraang pag-uugali.
