Ang "Stochastic" ay isang salita na ginagamit ng mga pisiko, matematika at iba pang mga siyentipiko upang ilarawan ang mga proseso na mayroong isang elemento ng pagkakataon. Ang pinagmulan nito ay sinaunang Griyego. Isinalin, nangangahulugang "magagawang hulaan."
Kahulugan ng salitang "stokastik"

Ang "Stochastic" ay isang konsepto na ginagamit sa maraming iba't ibang larangan ng agham. Nangangahulugan ito ng randomness, randomness, kawalan ng katiyakan ng isang bagay. Sa etika ni Aristotle (ang kanyang eskultura na eskultura ay ipinakita sa itaas), ang konsepto ng "stochastic" ay isang kahulugan na tumutukoy sa kakayahang hulaan. Malinaw, ginamit ito ng mga matematiko sa batayan na ang elemento ng pagkakataon ay lilitaw lamang kung kinakailangan upang hulaan. Ang salitang "stochastic" ay isang konsepto na tinukoy sa New International Dictionary bilang "conjectural."
Kaya, mapapansin na ang teknikal na kahulugan ng konseptong ito ay hindi eksaktong tumutugma sa bokabularyo (lexical) na kahulugan nito. Ang ilang mga may-akda ay gumagamit ng expression na "stochastic process" bilang isang kasingkahulugan para sa salitang "random na proseso".
Stochasticity sa matematika

Ang paggamit ng term na ito sa matematika ay kasalukuyang laganap. Halimbawa, mayroong tulad ng isang konsepto sa probabilidad na teorya bilang ang stochastic na proseso. Ang resulta nito ay hindi matukoy ng paunang estado ng sistemang ito.
Ang paggamit sa matematika ng konsepto ng "stochasticity" ay maiugnay sa mga gawa ng Vladislav Bortskevich. Siya ang gumamit ng term sa kahulugan ng "ilagay forward hypotheses." Sa matematika, lalo na sa isang seksyon ng agham na ito bilang teorya ng probabilidad, ang larangan ng random na pananaliksik ay gumaganap ng isang mahalagang papel. Mayroong, halimbawa, tulad ng isang bagay tulad ng isang stochastic matrix. Ang mga haligi o hilera ng matris na ito ay nagdaragdag sa isa.
Stochastic Mathematics (Pinansyal)
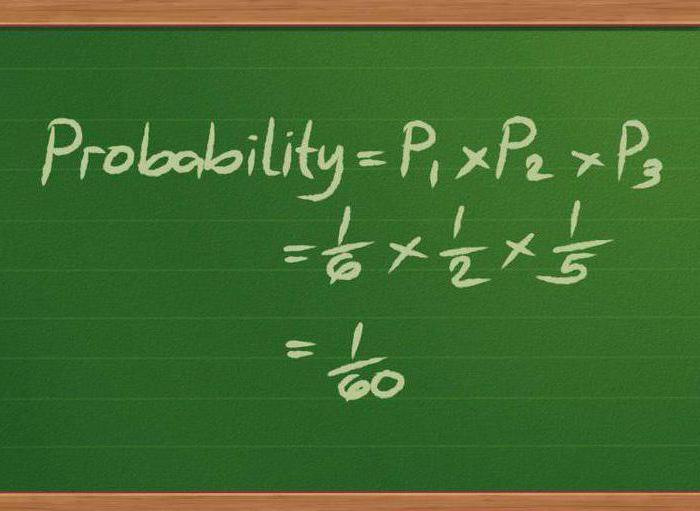
Sinusuri ng seksyong ito ng matematika ang mga istrukturang pinansyal na nagpapatakbo sa mga kondisyon ng kawalan ng katiyakan. Ito ay dinisenyo upang mahanap ang pinaka-nakapangangatwiran na pamamaraan ng pamamahala ng mga assets at istruktura sa pananalapi, na isinasaalang-alang ang mga kadahilanan tulad ng stochastic evolution, panganib, oras, atbp.
Sa agham, kaugalian na makilala ang mga sumusunod na istruktura at mga bagay na ginagamit sa matematika matematika bilang isang buo:
- mga kumpanya (halimbawa, mga kumpanya);
- mga indibidwal;
- mga tagapamagitan na istruktura (pondo ng pensyon, mga bangko);
- merkado sa pananalapi.
Ang pangunahing bagay ng pag-aaral ng stokastikong pinansiyal na matematika ay tiyak na ang huli sa kanila. Ang seksyon na ito ay batay sa mga naturang disiplina bilang istatistika ng mga random na proseso, teorya ng mga random na proseso, atbp.
Sa kasalukuyan, kahit na ang mga tao na malayo sa agham, mahusay na kilala mula sa maraming mga balita at mga pahayagan sa media na ang mga halaga ng tinatawag na pandaigdigang mga indeks sa pananalapi (halimbawa, ang index ng Dow Jones), ang mga presyo ng stock ay nagbabago nang sapalaran. Ginawa ni L. Bachelier ang unang pagtatangka upang ilarawan gamit ang matematika ang ebolusyon ng mga presyo ng stock. Ang kanyang stochastic na pamamaraan ay batay sa teorya ng posibilidad. Ang disertasyon ni L. Bachelier, na nagtatanghal ng pagtatangkang ito, ay nai-publish noong 1900. Napatunayan ng siyentipiko ang pormula na kasalukuyang kilala bilang patas na halaga ng halaga para sa mga pagpipilian sa tawag. Sinasalamin nito ang posibilidad na stochastic.
Ang mga mahahalagang ideya na kasunod na humantong sa paglitaw ng isang mabisang teorya sa pamilihan ay ipinakita sa gawain ni M. Kendall, na inilathala noong 1953. Tinukoy ng papel na ito ang isyu ng mga dinamikong presyo ng stock. Inilalarawan ito ng mananaliksik gamit ang mga proseso ng stokastik.
Stochasticity sa Physics
Salamat sa mga pisika ng E. Fermi, S. Ulam, N. Metropolis at D.Malawakang ginagamit ang Neumann na pamamaraan ng Monte Carlo. Ang pangalan nito ay nagmula sa isang casino na matatagpuan sa parehong lungsod sa isang bansa tulad ng Monaco. Narito dito na humiram ng pera si Uncle Ulam para sa laro. Ang paggamit ng likas na pag-uulit at pagkakataong pag-aralan ang mga proseso ay katulad sa nangyayari sa isang casino.

Kapag inilalapat ang pamamaraang ito ng pagmomolde, ang isang probabilistikong analog ay unang hinanap. Bago ito, ang pagmomolde ay isinasagawa sa kabaligtaran na direksyon: ginamit ito upang mapatunayan ang resulta ng problemistikong deterministik na nakuha nang mas maaga. Bagaman ang mga katulad na pamamaraang umiiral bago natuklasan ang pamamaraan ng Monte Carlo, hindi sila sikat at pangkalahatan.
Si Enrico Fermi noong 1930 ay nag-apply ng mga stochastic na pamamaraan upang makalkula ang mga katangian ng neutron, na natuklasan lamang sa oras na iyon. Ang mga pamamaraan ng Monte Carlo ay kalaunan ay ginamit kapag nagtatrabaho sa proyekto ng Manhattan, bagaman sa oras na iyon ang mga kakayahan ng mga computer ay lubos na limitado. Sa kadahilanang ito, naging laganap sila pagkatapos lumitaw ang mga computer.
Mga senyas na may akto
Ang mga regular at stochastic signal ay may iba't ibang mga alon. Kung susukat namin muli ang huli, nakakakuha kami ng mga oscillation na may bagong hugis, na naiiba sa nauna, ngunit nagpapakita ng isang pagkakatulad sa mga mahahalagang tampok. Ang isang halimbawa ng isang stochastic signal ay ang pag-record ng mga oscillations ng alon ng dagat.
Bakit kailangang pag-usapan ang tungkol sa mga hindi pangkaraniwang signal na ito? Ang katotohanan ay na sa pag-aaral ng mga awtomatikong sistema, sila ay mas karaniwan kaysa sa hinulaang.
Stochasticity at Artipisyal na Intelligence
Stochastic artipisyal na programa ng intelektwal ay gumagana gamit ang mga pamamaraan ng probabilistic. Ang mga algorithm tulad ng stochastic optimization o neural network ay maaaring mabanggit bilang isang halimbawa. Ang parehong naaangkop sa simulated annealing at genetic algorithm. Sa lahat ng mga kasong ito, ang stochasticity ay maaaring mapaloob sa problema tulad ng tulad o sa pagpaplano ng isang bagay sa ilalim ng kondisyon ng kawalan ng katiyakan. Ang deterministikong kapaligiran para sa isang ahente ng pagmomolde ay mas simple kaysa sa stochastic.

Kaya, tulad ng nakikita natin, ang konsepto ng interes sa amin ay ginagamit sa maraming larangan ng agham. Inilista namin at nailalarawan lamang ang mga pangunahing lugar ng application nito. Ang pag-aaral ng lahat ng mga prosesong ito, nakikita mo, ay napakahalaga at may kaugnayan. Iyon ang dahilan kung bakit ang konsepto ng interes sa amin ay malamang na magamit sa mahabang panahon sa agham.








