Pagtatasa ng korelasyon at regression: halimbawa, mga gawain, aplikasyon. Paraan ng pag-ugnay sa ugnayan at regression

Pagtatasa ng Pagkabagabag sa Pagduduwal - Ito ay isa sa mga pinaka-karaniwang pamamaraan para sa pag-aaral ng kaugnayan sa pagitan ng mga halagang numero. Ang pangunahing layunin nito ay upang mahanap ang ugnayan sa pagitan ng dalawang mga parameter at antas nito sa kasunod na derivation ng equation. Halimbawa, mayroon kaming mga mag-aaral na pumasa sa pagsusulit sa matematika at Ingles. Maaari kaming gumamit ng ugnayan upang matukoy kung ang tagumpay ng isang pagsubok ay nakakaapekto sa mga resulta sa ibang paksa. Tungkol sa pagsusuri ng regression, nakakatulong upang mahulaan ang mga marka sa matematika batay sa mga puntos na nakapuntos sa isang pagsusulit sa Ingles, at kabaligtaran.

Ano ang isang tsart ng ugnayan?

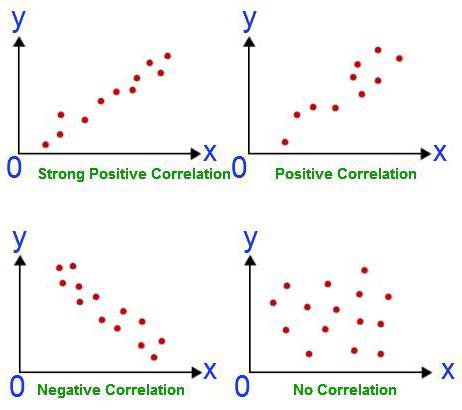
Ang anumang pagsusuri ay nagsisimula sa koleksyon ng impormasyon. Ang higit pa, mas tumpak ang resulta na nakuha sa pagtatapos. Sa halimbawa sa itaas, mayroon kaming dalawang disiplina kung saan kailangang pumasa ang isang mag-aaral. Ang kanilang rate ng tagumpay ay isang pagtatantya. Ang pagsusuri sa correlation-regression ay nagpapakita kung ang resulta ng isang paksa ay nakakaapekto sa mga puntos na nakapuntos sa ikalawang pagsusulit. Upang masagot ang katanungang ito, kinakailangan upang pag-aralan ang mga rating ng lahat ng mga mag-aaral na kahanay. Ngunit kailangan mo munang magpasya sa nakasalalay na variable. Sa kasong ito, hindi ito mahalaga. Ipagpalagay na nangyari ang isang pagsusulit sa matematika kanina. Ang mga puntos sa ito ay isang malayang variable (ipinagpaliban ang mga ito kasama ang abscissa). Ang Ingles ay nasa iskedyul mamaya. Samakatuwid, ang mga pagtatantya batay dito ay isang dependant variable (ay naka-plot sa kahabaan ng ordinate). Ang higit pang graph na nakuha na mukhang isang tuwid na linya, mas malakas ang linear correlation sa pagitan ng dalawang napiling mga halaga. Nangangahulugan ito na ang mga mag-aaral sa matematika ay mas malamang na makakuha ng mga fives sa pagsusulit sa Ingles.

Mga pagpapalagay at Pagpapasimpleng

Ang pamamaraan ng pag-ugnay sa ugnayan at regression ay nagsasangkot ng paghahanap ng isang kaugnay na relasyon. Gayunpaman, sa unang yugto, kailangan mong maunawaan na ang mga pagbabago sa parehong dami ay maaaring sanhi ng ilang pangatlo, hindi pa isinasaalang-alang ng mananaliksik. Maaari ding magkaroon ng mga di-magkakasunod na ugnayan sa pagitan ng mga variable, samakatuwid, ang pagkuha ng isang koepisyent na katumbas ng zero ay hindi ang pagtatapos ng eksperimento.

Pagkakaugnay sa linya ng Pearson

Ang koepisyent na ito ay maaaring magamit napapailalim sa dalawang kundisyon. Ang una - lahat ng mga halaga ng mga variable ay mga makatwirang numero, ang pangalawa - inaasahan na ang mga halaga ay nagbabago proporsyonal. Ang koepisyent na ito ay palaging nasa pagitan ng -1 at 1. Kung ito ay mas malaki kaysa sa zero, pagkatapos ay mayroong isang direktang proporsyonal na pag-asa, mas mababa - inversely, pantay - ang mga halagang ito ay hindi nakakaapekto sa isa't isa sa anumang paraan. Ang kakayahang kalkulahin ang tagapagpahiwatig na ito ay ang batayan ng pagsusuri sa ugnayan at regression. Sa kauna-unahang pagkakataon, ang koepisyent na ito ay binuo ni Karl Pearson batay sa ideya ni Francis Galton.

Mga Katangian at Pag-iingat

Ang coefficient ng correlation ni Pearson ay isang malakas na tool, ngunit dapat din itong gamitin nang may pag-iingat. Ang mga sumusunod na babala ay ginagamit nito:

1. Ang koepisyent ng Pearson ay nagpapahiwatig ng pagkakaroon o kawalan ng isang guhit na relasyon. Ang pagtatasa ng korelasyon-regression ay hindi nagtatapos doon, maaari itong lumingon na ang mga variable ay magkakaugnay na magkakaugnay.
2. Ang isa ay dapat maging maingat sa pagbibigay kahulugan sa halaga ng koepisyent. Ang isang ugnayan ay matatagpuan sa pagitan ng laki ng binti at antas ng IQ.Ngunit hindi ito nangangahulugan na ang isang tagapagpahiwatig ay tumutukoy sa isa pa.
3. Ang koepisyent ng Pearson ay walang sasabihin tungkol sa sanhi ng relasyon sa pagitan ng mga tagapagpahiwatig.

Koepisyentong ugnayan ng ranggo ng Spearman

Kung ang isang pagbabago sa halaga ng isang tagapagpahiwatig ay humahantong sa isang pagtaas o pagbawas sa halaga ng isa pa, nangangahulugan ito na may kaugnayan sila. Ang pagsusuri sa correlation-regression, isang halimbawa kung saan ibibigay sa ibaba, ay tiyak na konektado sa mga naturang mga parameter. Binibigyang-daan ka ng ranggo ng ranggo na gawing simple ang mga kalkulasyon.

Pagtatasa ng korelasyon at regression: isang halimbawa

Ipagpalagay na mayroong isang pagtatasa ng pagganap ng sampung negosyo. Mayroon kaming dalawang hukom na nagbibigay sa kanila ng mga puntos. Ang pag-ugnay ng ugnayan at regression ng negosyo sa kasong ito ay hindi maaaring isagawa batay sa koepisyent ng linear na Pearson. Hindi kami interesado sa relasyon sa pagitan ng mga rating ng mga hukom. Mahalaga ang ranggo ng mga negosyo ayon sa mga hukom.

Ang ganitong uri ng pagsusuri ay may mga sumusunod na pakinabang:

• Ang Nonparametric form ng mga relasyon sa pagitan ng pinag-aralan na dami.
• Dali ng paggamit, dahil ang mga ranggo ay maaaring maiugnay kapwa sa pataas na pagkakasunud-sunod ng halaga at pababang pagkakasunud-sunod.

Ang tanging kinakailangan ng ganitong uri ng pagsusuri ay ang pangangailangan upang mai-convert ang mapagkukunan ng data.

Mga problema sa aplikasyon

Ang pagsusuri sa ugnayan at regression ay batay sa mga sumusunod na pagpapalagay:

• Ang mga obserbasyon ay itinuturing na independiyenteng (isang limang-tiklop na pagkawala ng "agila" ay hindi nakakaapekto sa resulta ng susunod na barya na pitik).
• Sa pagtatasa ng ugnayan, ang parehong mga variable ay itinuturing na random. Sa regression - isa lamang (nakasalalay).
• Kapag sinusubukan ang isang hypothesis, dapat sundin ang isang normal na pamamahagi. Ang pagbabago sa umaasa variable ay dapat na pareho para sa bawat halaga sa abscissa.
• Ang diagram ng ugnayan lamang ang unang pagsubok ng hypothesis tungkol sa ugnayan sa pagitan ng dalawang serye ng mga parameter, at hindi ang pangwakas na resulta ng pagsusuri.

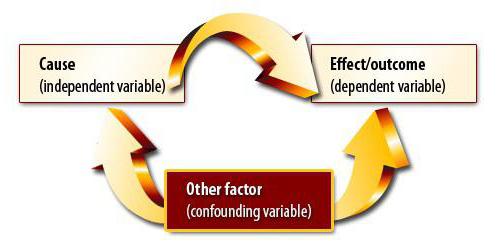
Pag-asa at sanhi

Ipagpalagay na kinakalkula namin ang koepisyent ng ugnayan ng dami ng pag-export at GDP. Ito ay naging pantay sa modulo ng pagkakaisa. Natapos na ba natin ang pagtatasa ng ugnayan at regression hanggang sa wakas? Syempre hindi. Ang resulta na nakuha ay hindi nangangahulugang sa lahat na ang GDP ay maipahayag sa pamamagitan ng pag-export. Hindi pa namin napatunayan ang isang sanhi ng relasyon sa pagitan ng mga tagapagpahiwatig. Pagtatasa ng correlation-regression - pagtataya ng mga halaga ng isang variable batay sa isa pa. Gayunpaman, kailangan mong maunawaan na madalas na maraming mga kadahilanan ang nakakaapekto sa parameter. Tinutukoy ng export ang GDP, ngunit hindi lamang ito. May iba pang mga kadahilanan. Narito mayroong isang ugnayan, at isang relasyon na sanhi, kahit na nababagay para sa iba pang mga sangkap ng gross domestic product.

Ang isa pang sitwasyon ay mas mapanganib. Sa UK, isang survey ay isinagawa na nagpapakita na ang mga bata na ang mga magulang na naninigarilyo ay mas madalas na nagkasala. Ang konklusyon na ito ay batay sa isang malakas na ugnayan sa pagitan ng tagapagpahiwatig. Ngunit tama ba siya? Una, maaaring maging kabaligtaran ang pag-asa. Ang mga magulang ay maaaring magsimula sa paninigarilyo dahil sa pagkapagod mula sa katotohanan na ang kanilang mga anak ay patuloy na nagkakaroon ng mga pagbabago at nilabag ang batas. Pangalawa, ang parehong mga parameter ay maaaring dahil sa pangatlo. Ang ganitong mga pamilya ay kabilang sa mababang mga klase sa lipunan, na kung saan ay nailalarawan sa parehong mga problema. Samakatuwid, batay sa ugnayan, hindi maaaring tapusin na mayroong isang sanhi ng relasyon.

Bakit gumagamit ng pagsusuri ng regression?

Ang pag-asa sa correlation ay nagsasangkot ng paghahanap ng mga relasyon sa pagitan ng dami. Ang sanhi ng relasyon sa kasong ito ay nananatili sa likod ng mga eksena. Ang mga gawain ng ugnayan sa korelasyon at regresyon ay nagkakasabay lamang sa mga tuntunin sa pagkumpirma ng pagkakaroon ng isang relasyon sa pagitan ng mga halaga ng dalawang dami. Gayunpaman, sa una ang mananaliksik ay hindi binibigyang pansin ang posibilidad ng isang relasyon na sanhi. Ang pagsusuri ng pagkadismaya ay palaging may dalawang variable, kung saan ang isa ay nakasalalay. Nagaganap ito sa maraming yugto:

1. Ang pagpili ng tamang modelo gamit ang hindi bababa sa mga parisukat na pamamaraan.
2. Pagmula ng isang equation na naglalarawan ng epekto ng isang pagbabago sa isang independiyenteng variable sa iba pa.

Halimbawa, kung pag-aralan natin ang epekto ng edad sa paglaki ng tao, kung gayon ang pagtatasa ng regression ay makakatulong na mahulaan ang mga pagbabago sa mga nakaraang taon.

Linear at maraming regresyon

Ipagpalagay na ang X at Y ay dalawang magkakaugnay na variable. Ang pagsusuri ng pagkadismaya ay nagbibigay-daan sa amin upang mahulaan ang laki ng isa sa mga ito batay sa mga halaga ng iba pa. Halimbawa, ang kapanahunan at edad ay nakasalalay na mga sintomas. Ang ugnayan sa pagitan ng mga ito ay makikita gamit ang linear regression. Sa katunayan, maaari mong ipahayag ang X sa pamamagitan ng Y o kabaligtaran. Ngunit madalas lamang ang isa sa mga linya ng regression ay tama. Ang tagumpay ng pagsusuri higit sa lahat ay nakasalalay sa tamang pagpapasiya ng independyenteng variable. Halimbawa, mayroon kaming dalawang mga tagapagpahiwatig: ani at pag-ulan. Mula sa pang-araw-araw na karanasan, malinaw na ang una ay nakasalalay sa pangalawa, at hindi kabaliktaran.

Pinapayagan ka ng maraming regresyon na makalkula ang isang hindi kilalang halaga batay sa mga halaga ng tatlo o higit pang mga variable. Halimbawa, ang ani ng bigas bawat ektarya ng lupa ay nakasalalay sa kalidad ng butil, pagkamayabong ng lupa, mga pataba, temperatura, at pag-ulan. Ang lahat ng mga parameter na ito ay nakakaapekto sa pangkalahatang resulta. Upang gawing simple ang modelo, ang mga sumusunod na pagpapalagay ay ginagamit:

• Ang relasyon sa pagitan ng independyente at nakakaimpluwensyang mga katangian ay magkatugma.
• Ang Multicollinearity ay hindi kasama. Nangangahulugan ito na ang mga variable na umaasa ay hindi magkakaugnay.
• Homoskedasticity at normalidad ng serye ng mga numero.

Ang paggamit ng correlation at regression analysis

Mayroong tatlong pangunahing mga kaso ng paggamit ng pamamaraang ito:

1. Pagsubok sa mga kaswal na relasyon sa pagitan ng dami. Sa kasong ito, tinutukoy ng mananaliksik ang mga halaga ng variable at nalaman kung nakakaapekto sa pagbabago sa umaasang variable. Halimbawa, maaari mong bigyan ang mga tao ng iba't ibang mga dosis ng alkohol at masukat ang kanilang presyon ng dugo. Sa kasong ito, alam ng mananaliksik na ang una ay ang sanhi ng pangalawa, at hindi kabaliktaran. Ang pag-aaral sa correlation-regression ay nagbibigay-daan sa iyo upang makita ang isang direktang proporsyonal na guhit na relasyon sa pagitan ng dalawang variable na ito at kumuha ng isang formula na naglalarawan nito. Sa kasong ito, ang mga halaga na ipinahayag sa ganap na magkakaibang mga yunit ng pagsukat ay maaaring ihambing.
2. Ang paghahanap ng isang relasyon sa pagitan ng dalawang variable na hindi nagpapalawak ng isang sanhi na relasyon sa kanila. Sa kasong ito, walang pagkakaiba sa kung anong sukat ng tawag ng mananaliksik na nakasalalay. Bukod dito, sa katotohanan, maaaring lumitaw na ang dalawa sa kanila ay apektado ng pangatlong variable, samakatuwid ay nagbabago sila nang proporsyonal.
3. Pagkalkula ng mga halaga ng isang dami batay sa isa pa. Ito ay batay sa isang equation kung saan ang mga kilalang numero ay nahalili.

Sa gayon, ang pagsusuri ng ugnayan ay nagsasangkot ng paghahanap ng isang koneksyon (hindi sanhi) sa pagitan ng mga variable, at ang pagtatasa ng regression ay nagpapaliwanag sa ito, na madalas na gumagamit ng isang pag-andar sa matematika.