Сложена реч "екстраполација" састоји се од две једноставне речи. Прво на латинском језику звучи додатно и значи „напољу“, „за“, „споља“. Друго на истој латино звучи полире и значи „променити“, „исправити“, „глатко“. Генерално, екстраполација се може дефинисати као вредност изван две дате тачке. Сматра се проценом онога што се извлачи из познатих чињеница које проширују податке у непознато подручје како би се постигао планирани резултат. Овај концепт се такође може приписати предвиђању слике будућности, претпостављајући истинитост садашњих и прошлих трендова.
Метода екстраполације претпоставља да ће подаци или запажања у будућности и даље бити слична. Тако се могу предвидјети будући резултати. Може се сматрати математичком хипотезом. Екстраполација користи податке и чињенице о конкретној ситуацији и даје предвиђања шта се на крају може догодити.
Историја екстраполације

Ову методу често називају Рицхардсон-овом екстраполацијом или Ромберговим методом. Али то није сасвим тачно, јер су вековима постојале сличне нумеричке методе за решавање таквих проблема. Стога, познати Рицхардсон х2 (екстраполација за нумеричко решење) није први. Сличан метод био је применљив у Хуигенсовим прорачунима већ 1654. Сам термин "екстраполација" први пут је сковао Тхомас Д. Цларесон 1959. године у књизи о науци и фантастици.
Методе екстраполације могу се схватити као проширење података или процеса који сугеришу да ће се сличан процес применити и ван њих. Екстраполација је важан концепт који се користи не само у математици, већ иу другим областима, попут социологије, психологије, прогнозирања. На пример, возач обично екстраполира услове вожње ван свог вида. Екстраполација се може приписати методи у којој се вредности података сматрају тачкама к1, к2 ..., кн, а затим се вредност приближава граници одређеног распона тачака.
Предности употребе:
- Једноставна метода предвиђања.
- Није потребно много података.
- Брза и јефтина аналитика.
Метода постоји у статистици. Ако се било које вредности повремено уклањају, одговор се приближава следећој тачки података. Пример методе екстраполације је временска прогноза која испитује позадину података и екстраполира предвиђени модел будућности. Још једноставнији пример, ако имате информације о недељом, понедељком и уторком, можете екстраполирати среду или четвртак.
Недостаци употребе екстраполације:
- Непоузданост, ако постоје значајна колебања историјских података.
- Претпоставка да ће се прошли тренд наставити у будућности тешко је могућа у многим конкурентним пословним окружењима.
- Занемарује факторе квалитета, као што су промене укуса и моде.
Убрзање секвенци
Методе екстраполације су креирање тангенцијалне линије на крају познатих података и ширење изван овог подручја. Као и интерполација, екстраполација користи многе методе за које је потребно претходно знање о процесу који ствара постојеће тачке података. Метода укључује линеарну и полиномну екстраполацију, конике и екстраполацију француске криве.
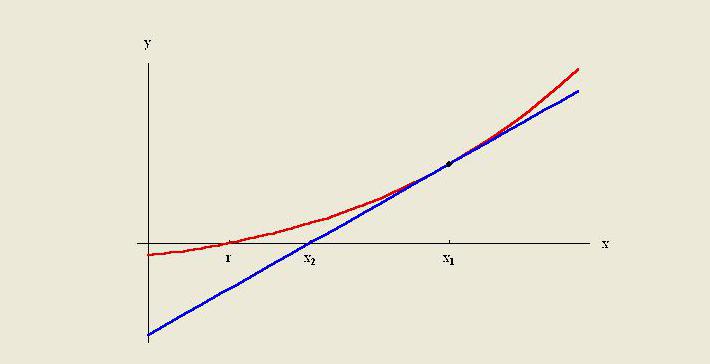
У правилу је квалитета одређене методе ограничена претпоставкама о функцији. У нумеричкој анализи, Рицхардсон-ова екстраполација је метода убрзања секвенце која се користи за побољшање брзине конвергенције.Име је добио по Левису Фри Рицхардсону. Он је увео технику израчуна почетком 20. века, чија се корисност за практичне прорачуне тешко може прецијенити.
Практичне примене Рицхардсон-ове екстраполације укључују Ромбергову интеграцију, која се примењује на трапезоидно правило и алгоритам Буллиерс-Стоехр за решавање обичних диференцијалних једначина.
Линеарна метода
Метода линеарне екстраполације је корисна када је одређена линеарна функција. То се изводи цртањем тангенцијалне линије на крајњој тачки датог графа и ширењем даље од њега. Ова метода екстраполације у прогнозирању даје добре резултате када тачка коју треба предвидјети није предалеко од података. Линеарна интерполација је корисна у проналажењу вредности између задатих тачака. Може се сматрати „попуњавањем празнина“ у табели података.
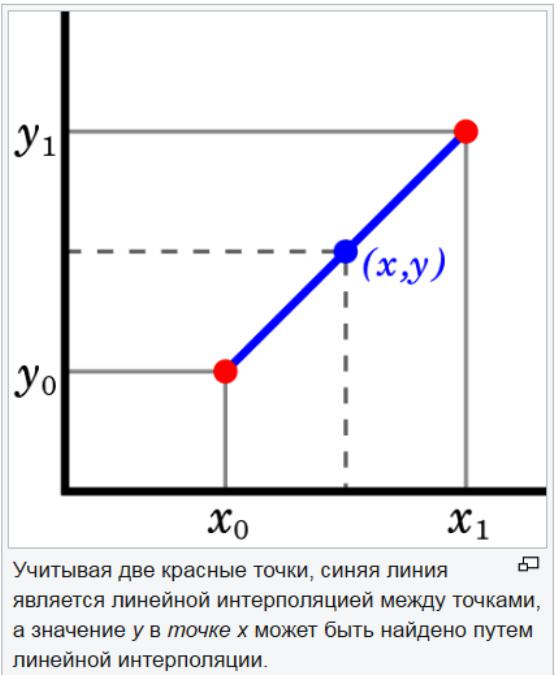
Стратегија линеарне интерполације је употреба равне линије за повезивање познатих тачака вредности са обе стране непознате. Линеарна интерполација није тачна за нелинеарне параметре. Ако се тачке у скупу података промијене за велику количину, линеарна интерполација може дати погрешну процјену.
Линеарна екстраполација може помоћи у процени вредности које су веће или ниже од вредности у скупу података. Његова стратегија је да користи подскуп података уместо целог скупа. За ову врсту вредности корисно је применити метод екстраполације у прогнозирању користећи последње две или три тачке за процену вредности која прелази распон података.
Полиномне и коничне екстраполације
Познато је да три тачке дају јединствени полином. Полиномна кривуља се може наставити након завршетка таквих података. Обично се изводи Невтоновом методом са коначном разликом или употребом Лагрангеове интерполацијске формуле. Полином вишег реда треба екстраполирати с дужном пажњом, јер постоји велика могућност погрешке код полиномске екстраполације. Ако се то догоди, процена грешке ће се експоненцијално повећавати са степеном полинома.
У математици, минимална полиномска екстраполација је трансформација секвенце која се користи за убрзавање конвергенције. Иако је Аиткенова метода најпознатија, она често не успева, посебно за векторске секвенце. У овом случају се изводи итерација која конструира матрицу. Њене колоне су разлике.

На пример, метода екстраполације за конусни пресек може се извести помоћу 5 тачака означених на крају података. У случају да је конични пресјек круг или елипса, тада ће се петљати и поново се ујединити са собом. Парабола или хипербола се никада не сијеку. Али они се могу савити око осе Кс. Екстраполација конуса може се обавити на папиру са конусним пресеком или помоћу рачунара.
Метода математичке евалуације
У овом методу екстраполације предвиђа се вредност за базни период. Доље описане радње систем аутоматски изводи и нису видљиве кориснику. Намјера је да се прецизира алгоритам који приказује очекиване вриједности из количине похрањене у систему и предвиђа резултат мјерења бројила.
Екстраполација помоћу дефиниције количине поступка изводи се функцијом: Ит = ф (ии, т, ај).
Као основа за екстраполацију додају се заокружени подаци типичног основног периода похрањени у резултатима очитања. Систем одређује тежину Ит података временских серија у т (време прогнозираног периода) да би се добило исправно решење екстраполацијом. Тамо где су узете референтне тачке, ии - ниво серије и ај - параметар једнаџбе тренда.
Предвиђање функција
Метода фиксирања статистичке кривуље применљива је на предвиђање функционалности.Статистички поступци одговарају прошлим подацима једне или више математичких функција, као што су линеарна, логаритамска, Фоуријева или експоненцијална. Најбољи се бирају статистичким тестом. Тада се ова математичка веза екстраполира методом математичке екстраполације. Један од најлакших начина за добијање грубих процена будућих (или прошлих) услова је екстраполирање података који се временом мењају.
На пример, ако треба да направите грубу процену будућих нивоа загађивача у питкој води за 20 година унапред, можете екстраполирати овај тренд у последњих 20 година. Исто се примећује ако требате проценити учесталост пушења или рака плућа у позадини у будућности. Прогноза се може израчунати трендовима последњих година. Екстраполације овог типа могу се извршити употребом мање сложених метода. У многим случајевима (посебно у областима маркетинга и управљања пословањем), метода екстраполације традиционално се користи, на пример, прегледом најновијих података и интуитивном проценом шта се мисли у будућности.
Методе засноване на правилима могу се такође користити применом скупа унапред дефинисаних принципа или очекивања заснованих на прелиминарном разумевању система и узимајући у обзир најновије податке за интерпретацију будућих догађаја.
Уз било коју метод екстраполације важан је опрез због присуства бројних несигурности. Сваки поступак екстраполације заснован је на претпоставци да су доступне поуздане информације о прошлим подацима и знању. Сходно томе, будућност је одређена истим факторима који су дјеловали раније.
Грешке предвиђања
Заблуда екстраполације (тачније погрешна неоправдана екстраполација) догађа се када се феномен одговоран за бројне тривијалне локалне ефекте чита као велике глобалне појаве. Други разлог за грешку је тај што се понекад генерализована правила изводе из премало чињеница. Дакле, Дарвинова теорија еволуције фантастичан је пример примене методе екстраполације у којој се објављују механизми случајних промена и природне селекције да би се узео у обзир развој тако сложених структура као што су сисар визија или имуни систем живих организама.
Приликом покушаја тумачења резултата истраживања, научник треба да избегава екстраполацију изван распона података и да буде свестан основних претпоставки како би избегао прихватање неваљаних закључака. Генерално, екстраполација је легитимно научно средство. Постоје два аспекта која помажу у разликовању валидне и погрешне екстраполације. Вероватноћа погрешне екстраполације је већа када су добијени бодови за недовољно података за њену изградњу.
Екцел Статистички алати
Да бисте пронашли повезаност између година и резултата (на пример, у предузећу), можете да користите Екцел.
За ове задатке користе се статистички алати за екстраполацијско моделирање који су уграђени у све верзије Екцела, почевши од 97. Процедура:
- Унесите познате вредности, на пример, укупну продају за 2016-2017, ако их требате одредити за 2018. и 2020. годину.
- Инсталирајте анализу, функцију која захтева употребу додатка.
- Да бисте га инсталирали, издвојите из менија „Алатке“, „Додаци“.
- Проверите прозор услужног програма за анализу и потврдите са „ОК“.
- Измерите корелације између две серије.
- Екстраполација коју треба урадити има смисла само ако постоји јасан тренд (корелација) између два скупа бројева (година и продаја) методом екстраполирања трендова.
- Да бисте мерили ову корелацију, користите мени „Алати“, „Алат за анализу“.
- На листи „Алати за анализу“ изаберите „Анализа корелације“ и кликните „У реду“.
- У поље Инпут Ранге унесите анализирани распон, на пример А6: Б18, Екцел ће додати симбол „$“.
- У пољу "Излазне могућности" проверите опсег излаза и унесите га у суседно поље.
- Потврдите са ОК.
- Екцел креира низ од два реда у два ступца. Пронађите израчунату вредност (на пример, 0,981). Пошто је ова вредност близу 1, то значи да постоји јака повезаност између година и података о продаји. Ако корисник прими вриједност близу нуле, то ће значити да се тренд не појављује. У овом случају екстраполација нема смисла.
- Почиње евалуација будућих вредности.
- Одаберите жељени распон и кликните гумб "Чаробњак за графиконе".
- Одаберите графикон (на пример, облаци тачака) и кликните Финисх.
Употреба покретних просека
Ове две методе екстраполације укључују широку употребу података о продаји како би се предвиђала будућност. Помична просјечна вриједност узима низ података и „изглађује“ флуктуације у њима. Циљ је извући екстремност података из периода у период. Помични просјеци често се рачунају квартално или недељно. За предвиђање будућих вредности, екстраполација укључује употребу трендова утврђених историјским подацима. Главна претпоставка екстраполације је да ће се узорак наставити у будућности, осим ако стварни докази не показују другачије. Да бисте детаљније разумели ове методе, можете размотрити графикон који приказује продају гадгета за велика предузећа од 2012. до 2015. године.
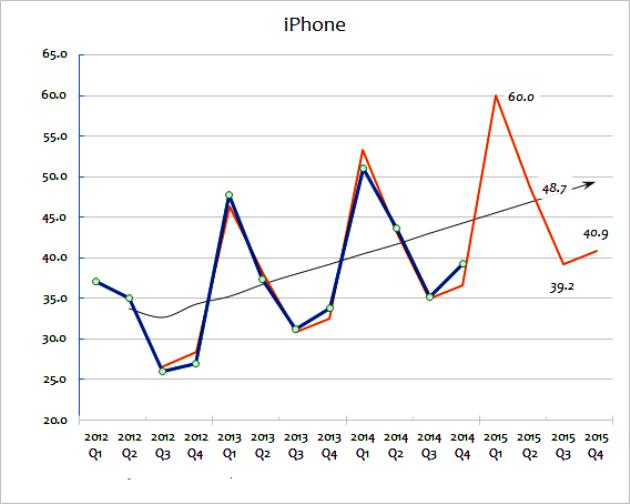
Ова метода екстраполације израчуна показује стварни износ продаје. Као што видите, укупна количина продаје варира из године у годину, мада можете претпоставити (гледајући податке) да постоји општи тренд раста продаје. Црна црта показује клизни просјек. То се израчунава тако што се додају последње године продаје (нпр. К1 + К2 + К3 + К4), а затим се поделе са четири.
Ова метода изглађује годишње промене и даје добру представу о општем тренду годишње продаје. Помични просјек помаже у назнаци тренда раста израженог у процентима. Управо ће се та екстраполација први користити за предвиђање будуће продаје. То се може математички урадити помоћу табеле. Алтернативно, екстраполирани тренд може се једноставно приказати на графикону као груба процена.
Корелација трендова
Увек је једна технологија претеча друге. То се дешава када напредак у технологији претходника може бити усвојен следбеном технологијом. Када постоје такви односи, знање о променама у технологији претходника може се користити за предвиђање напретка следбеника технологије у будућности. Поред тога, екстраполација прекурсора омогућава предвиђање наставка следења изван временског одлагања.
У овом се случају користи метода екстраполације трендова у којој се, на примјер, упоређују трендови у брзини војних и транспортних авиона. Други пример предвиђања корелације трендова је предвиђање величине и снаге будућих рачунара на основу напретка у микроелектронској технологији. Понекад технологија следбеника зависи од неколико технологија претеча, али не и од једног претходника.
Фиксне комбинације претходника могу утицати на промену низа, али чешће комбинације нису фиксне, а уноси претходника се разликују и по комбинацији и по снази. На пример, до повећања брзине авиона може доћи услед побољшања мотора, материјала, контрола, горива, аеродинамике и различитих комбинација ових фактора.
Пример корелационе прогнозе добијене екстраполирањем трендова: укупни путнички километри, укупне географске миље и просечна сила за слетање.Екстраполација статистички одређених трендова омогућава објективан приступ прогнозирању. Међутим, овај приступ има озбиљна ограничења и замке. Било какве грешке или нетачни избори извршени приликом одређивања историјских података одразиће се у прогнози, што смањује њену вредност.
Апликације, атрибути и ограничења
Метод екстраполације спада у област предвиђања. Он сугерише да ће се обрасци који су постојали у прошлости наставити и у будућност, те да су ти обрасци правилни и могу да се мере. Другим речима, прошлост је добар показатељ будућности. Апликације су корисне за развијање основних података.
Атрибути и ограничења су једноставни и јефтини алати за прорачун, као и сложени теоријски модели.
- Процесни подаци - графикони и запажања.
- Кључно је имати добру базу података и разумевање структуре унутар ње.
- Техника је најбоље уклапање, однос и тако даље.
Привремени стандардни статистички поступци не воде тачном одабиру трендова које прогностичар са удобношћу може екстраполирати, обављајући прогнозу екстраполацијом. У таквим случајевима прогностичар може „прилагодити“ статистичке резултате користећи процене. Такође може у потпуности игнорисати статистику и екстраполирати читав тренд заснован на процени.
Овако створена предвиђања мање су тачна од статистичких предвиђања, али нису нужно и незадовољавајућа. Један пример такве екстраполације тренда квалитета је предвиђање сложености летелица. Покушаји да се квантификује овај тренд нису били успешни. Али проценат покретних или подесивих делова авиона екстраполиран је фреквенцијом којом су такви елементи уведени у прошлости. Те прогнозе су биле прилично тачне.
Специфичне техничке промене се не могу предвидети на овај начин, али степен промена може. Ово пружа корисне материјале за планирање, што указује на тренд у прошлом понашању.
