"Стохастичка" је реч коју физичари, математичари и други научници користе да опишу процесе који имају елемент шансе. Њено порекло је старогрчки. Преведено, значи „способна погодити“.
Значење речи „стохастички“

„Стохастички“ је концепт који се користи у многим различитим областима науке. То значи случајност, случајност, несигурност нечега. У етици Аристотела (његов кипарски портрет представљен је горе) концепт „стохастичког“ је дефиниција која се односи на способност погађања. Очигледно, математичари су га користили на основу тога да се елемент случајности појављује баш тамо када је то потребно. Реч "стохастички" је концепт који је у Новом међународном речнику дефинисан као "претпостављив".
Дакле, може се приметити да техничко значење овог концепта не одговара баш његовом вокабуларном (лексичком) значењу. Неки аутори користе израз „стохастички процес“ као синоним за термин „случајни процес“.
Стохастичност у математици

Употреба овог термина у математици тренутно је распрострањена. На пример, у теорији вероватноће постоји такав концепт као стохастички процес. Његов резултат се не може одредити почетним стањем овог система.
Употреба концепта "стохастичности" у математици се приписује делима Владислава Бортскевича. Он је тај термин користио у значењу "изнео хипотезе". У математици, посебно у таквом делу ове науке као што је теорија вероватноће, поље случајних истраживања игра важну улогу. На пример, постоји таква ствар као стохастичка матрица. Ступци или редови ове матрице сачињавају један.
Стохастичка математика (финансијска)
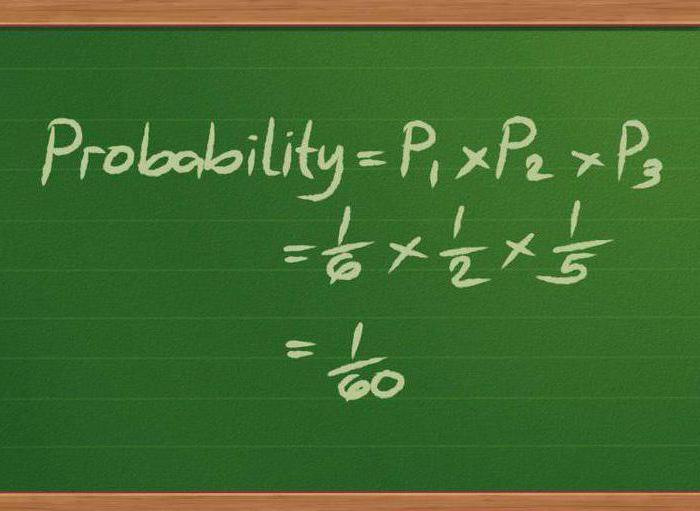
Овај одељак математике анализира финансијске структуре које делују у условима несигурности. Дизајниран је да нађе најрационалније методе управљања финансијском имовином и структурама, узимајући у обзир факторе као што су стохастичка еволуција, ризик, време итд.
У науци је уобичајено разликовати следеће структуре и објекте који се користе у финансијској математици у целини:
- фирме (на пример, компаније);
- појединци;
- посредничке структуре (пензиони фондови, банке);
- финансијска тржишта.
Главни предмет проучавања стохастичке финансијске математике је управо последњи од њих. Овај одељак заснован је на дисциплинама као што су статистика случајних процеса, теорија случајних процеса итд.
Тренутно је чак и људима далеко од науке познато из бројних вести и публикација у медијима да се вредности такозваних глобалних финансијских индекса (на пример, Дов Јонес индекс) цене акција мењају насумично. Л. Бацхелиер је први покушао да математиком опише развој цена акција. Његова стохастичка метода заснива се на теорији вероватноће. Дисертација Л. Бацхелиера која представља овај покушај објављена је 1900. године. Научник је доказао формулу која је тренутно позната као формула фер вредности за опције позива. Одраз је стохастичке вероватноће.
Важне идеје које су касније довеле до појаве ефикасне теорије тржишта представљене су у раду М. Кендалл, објављеном 1953. У овом раду обрађује се питање динамике цена акција. Истраживач га описује користећи стохастичке процесе.
Стохастичност у физици
Захваљујући физичарима Е. Фермију, С. Уламу, Н. Метрополису и Д.Неуманн се широко користи Монте Царло метода. Име му долази од казина смештеног у истом граду у земљи као што је Монако. Овде је ујак Улам позајмио новац за игру. Кориштење природе понављања и шанси за проучавање процеса слично је ономе што се догађа у касину.

Приликом примене ове методе моделирања прво се тражи вероватни аналог. Пре тога, моделирање је спроведено у супротном смеру: коришћено је за верификацију резултата раније добијених детерминистичких проблема. Иако су слични приступи постојали и пре открића методе Монте Царло, они нису били популарни и уопштени.
Енрицо Ферми 1930. године применио је стохастичке технике за израчунавање својстава неутрона, која су тек откривена у то време. Монте Царло методе су касније коришћене током рада на пројекту Менхетна, мада су у то време могућности рачунара биле значајно ограничене. Из тог разлога, они су постали широко распрострањени тек након што су се појавили рачунари.
Стохастички сигнали
Редовни и стохастички сигнали имају различите таласне облике. Ако поново измеримо последње, добићемо осцилације које имају нови облик, различит од претходног, али показују одређену сличност у битним карактеристикама. Пример стохастичког сигнала је снимање осцилација морских таласа.
Зашто је потребно разговарати о овим прилично необичним сигналима? Чињеница је да су они у истраживању аутоматских система још чешћи него што се предвиђало.
Стохастичност и вештачка интелигенција
Програми стохастичке вештачке интелигенције раде користећи вероватноће методе. Алгоритми попут стохастичке оптимизације или неуронске мреже могу се навести као пример. Исто се односи и на симулиране алгоритме жарења и генетичке алгоритме. У свим тим случајевима, стохастичност може бити садржана у проблему као таквом или у планирању нечега под условом несигурности. Детерминистичко окружење за средство за моделирање је једноставније од стохастичког.

Дакле, као што видимо, концепт који нас занима користи се у многим областима науке. Навели смо и окарактерисали само главна подручја његове примене. Проучавање свих ових процеса је, како видите, веома важно и релевантно. Зато ће се појам који нас занима вјероватно дуго користити у науци.








