"Stokastisk" er et ord som fysikere, matematikere og andre forskere bruker for å beskrive prosesser som har et tilfeldig element. Opprinnelsen er eldgammel gresk. Oversatt betyr det "i stand til å gjette."
Betydning av ordet "stokastisk"

"Stokastisk" er et konsept som brukes i mange forskjellige vitenskapsfelt. Det betyr tilfeldighet, tilfeldighet, usikkerhet om noe. I Aristoteles etikk (hans skulpturelle portrett er presentert ovenfor) er begrepet "stokastisk" en definisjon som refererer til evnen til å gjette. Åpenbart brukte matematikere det på grunnlag av at tilfeldighetselementet dukker opp akkurat når det er nødvendig å gjette. Ordet "stokastisk" er et begrep som er definert i New International Dictionary som "conjectural."
Dermed kan det bemerkes at den tekniske betydningen av dette konseptet ikke akkurat samsvarer med dets ordforråd (leksikalske) betydning. Noen forfattere bruker uttrykket "stokastisk prosess" som et synonym for uttrykket "tilfeldig prosess".
Stokastisitet i matematikk

Bruken av dette begrepet i matematikk er for tiden utbredt. For eksempel er det et slikt konsept i sannsynlighetsteori som den stokastiske prosessen. Resultatet av dette systemet kan ikke bestemmes.
Bruken i matematikk av begrepet "stokastisitet" tilskrives verkene til Vladislav Bortskevich. Det var han som brukte betegnelsen i betydningen "la frem hypoteser." I matematikk, spesielt i en slik del av denne vitenskapen som sannsynlighetsteori, spiller feltet for tilfeldig forskning en viktig rolle. Det er for eksempel noe som en stokastisk matrise. Kolonnene eller radene i denne matrisen legger opp til en.
Stokastisk matematikk (finansiell)
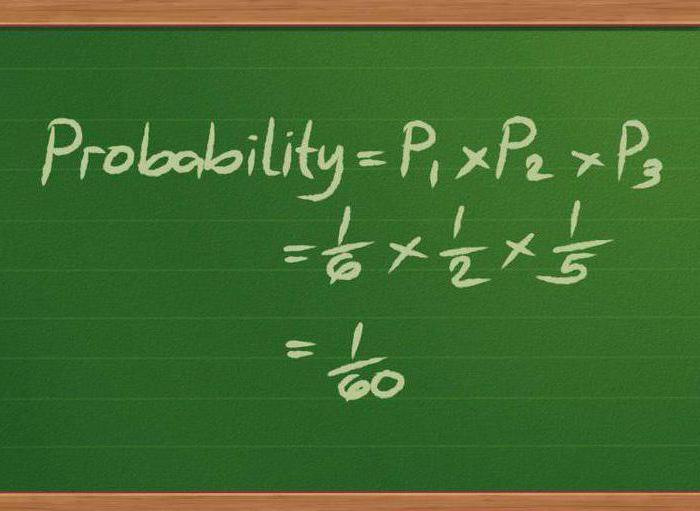
Denne delen av matematikken analyserer økonomiske strukturer som opererer i usikkerhetsmessige forhold. Den er designet for å finne de mest rasjonelle metodene for å forvalte finansielle eiendeler og strukturer, med hensyn til faktorer som stokastisk evolusjon, risiko, tid osv.
I naturfag er det vanlig å skille følgende strukturer og objekter som brukes i finansmatematikk som helhet:
- firmaer (for eksempel selskaper);
- enkeltpersoner;
- formidlingsstrukturer (pensjonsfond, banker);
- finansmarkeder.
Hovedobjektet med å studere stokastisk finansmatematikk er nettopp det siste av dem. Denne delen er basert på fagdisipliner som statistikk over tilfeldige prosesser, teori om tilfeldige prosesser, etc.
For tiden, selv folk langt fra vitenskap, er det kjent fra en rekke nyheter og publikasjoner i media at verdiene til de såkalte globale finansielle indeksene (for eksempel Dow Jones-indeksen), aksjekursene endres tilfeldig. L. Bachelier gjorde det første forsøket på å beskrive ved bruk av matematikk utviklingen i aksjekursene. Hans stokastiske metode er basert på sannsynlighetsteori. L. Bacheliers avhandling, som presenterer dette forsøket, ble utgitt i 1900. Forskeren har bevist formelen som for tiden er kjent som virkelig verdi-formelen for samtalealternativer. Det gjenspeiler den stokastiske sannsynligheten.
Viktige ideer som senere førte til fremveksten av en effektiv markedsteori ble presentert i arbeidet til M. Kendall, publisert i 1953. Denne artikkelen tar for seg spørsmålet om aksjekursdynamikk. Forskeren beskriver det ved hjelp av stokastiske prosesser.
Stokastisitet i fysikk
Takk til fysikere E. Fermi, S. Ulam, N. Metropolis og D.Neumann er mye brukt Monte Carlo-metoden. Navnet kommer fra et kasino som ligger i samme by i et land som Monaco. Det var her onkel Ulam lånte penger til spillet. Å bruke arten av repetisjon og sjanse til å studere prosesser ligner det som skjer i et kasino.

Når du bruker denne modelleringsmetoden, blir det først søkt etter en sannsynlig analog. Før dette ble modellering utført i motsatt retning: den ble brukt til å verifisere resultatet av det deterministiske problemet som ble oppnådd tidligere. Selv om lignende tilnærmelser fantes før oppdagelsen av Monte Carlo-metoden, var de ikke populære og generelle.
Enrico Fermi benyttet i 1930 stokastiske teknikker for å beregne egenskapene til nøytronet, som nettopp var blitt oppdaget på det tidspunktet. Monte Carlo-metodene ble senere brukt når du arbeidet med Manhattan-prosjektet, selv om datamaskinene på den tiden var betydelig begrenset. Av denne grunn ble de utbredt først etter at datamaskiner dukket opp.
Stokastiske signaler
Vanlige og stokastiske signaler har forskjellige bølgeformer. Hvis vi måler sistnevnte, får vi svingninger som har en ny form, som er forskjellig fra den forrige, men viser en viss likhet i essensielle funksjoner. Et eksempel på et stokastisk signal er registrering av havbølgesvingninger.
Hvorfor er det nødvendig å snakke om disse ganske uvanlige signalene? Fakta er at i studiet av automatiske systemer er de enda mer vanlige enn forutsagt.
Stokastisitet og kunstig intelligens
Stokastiske kunstige intelligensprogrammer bruker probabilistiske metoder. Algoritmer som stokastisk optimalisering eller nevrale nettverk kan nevnes som et eksempel. Det samme gjelder simulerte annealing og genetiske algoritmer. I alle disse tilfellene kan stokastisitet inneholdes i problemet som sådan eller ved å planlegge noe under betingelse av usikkerhet. Det deterministiske miljøet for et modelleringsmiddel er enklere enn stokastisk.

Så som vi ser, er begrepet interesse for oss brukt i mange vitenskapsfelt. Vi har listet opp og karakterisert bare hovedområdene for bruken. Studien av alle disse prosessene, ser du, er veldig viktig og relevant. Det er grunnen til at begrepet interesse for oss sannsynligvis vil bli brukt i lang tid i vitenskapen.








