Kata majmuk "ekstrapolasi" terdiri daripada dua perkataan mudah. Yang pertama dalam bahasa Latin bunyi tambahan dan bermaksud "di luar", "untuk", "di luar". Yang kedua dalam bahasa Latin sama bunyi polire dan bermaksud "perubahan", "meluruskan", "licin". Secara umumnya, ekstrapolasi boleh didefinisikan sebagai nilai di luar dua mata yang diberikan. Ia dianggap sebagai penilaian terhadap apa yang diekstrak daripada fakta yang diketahui bahawa mengembangkan data di kawasan yang tidak diketahui untuk mencapai keputusan yang diharapkan. Konsep ini juga boleh dikaitkan dengan ramalan imej masa depan, dengan menganggap kebenaran trend semasa dan masa lalu.
Kaedah ekstrapolasi mengandaikan bahawa data atau pemerhatian pada masa akan datang akan tetap sama. Oleh itu, keputusan masa depan boleh diramalkan. Ia boleh dianggap sebagai hipotesis matematik. Ekstrapolasi menggunakan data dan fakta situasi tertentu dan memberikan ramalan tentang apa yang mungkin berlaku pada akhirnya.
Sejarah Ekstrapolasi

Kaedah ini sering dirujuk sebagai ekstrapolasi Richardson atau kaedah Romberg. Tetapi ini tidak sepenuhnya betul, kerana selama berabad-abad terdapat kaedah berangka yang sama untuk menyelesaikan masalah tersebut. Oleh itu, Richardson terkenal h2 (extrapolation untuk penyelesaian berangka) bukan yang pertama. Kaedah yang serupa berlaku dalam pengiraan Huygens seawal tahun 1654. Istilah "ekstrapolasi" itu sendiri pertama kali dicipta oleh Thomas D. Clareson pada tahun 1959 dalam buku mengenai sains dan fiksyen.
Kaedah ekstrapolasi boleh difahami sebagai lanjutan data atau proses, yang menunjukkan bahawa proses yang sama akan digunakan di luarnya. Extrapolation adalah konsep penting yang digunakan bukan sahaja dalam matematik, tetapi juga di bidang lain, seperti sosiologi, psikologi, ramalan. Sebagai contoh, pemandu biasanya mengeksport keadaan memandu di luar visinya. Ekstrapolasi boleh dikaitkan dengan kaedah di mana nilai data dianggap sebagai mata x1, x2 ..., xn, dan kemudian nilai menghampiri had tertentu mata.
Manfaat penggunaan:
- Kaedah peramalan mudah.
- Tidak banyak data diperlukan.
- Analisis cepat dan murah.
Kaedah ini wujud dalam statistik. Jika sebarang nilai dikeluarkan secara berkala, jawapannya mendekati titik data seterusnya. Contoh kaedah ekstrapolasi ialah ramalan cuaca, yang meneliti latar belakang data dan mengekstrapulasi model masa depan yang diramalkan. Satu contoh yang lebih sederhana, jika anda mempunyai maklumat mengenai hari Ahad, Isnin dan Selasa, anda boleh mengeksplorasi hari Rabu atau Khamis.
Kelemahan penggunaan ekstrapolasi:
- Tidak boleh dipercayai, jika terdapat turun naik ketara dalam data sejarah.
- Anggapan bahawa trend masa lalu akan berterusan pada masa depan adalah tidak mungkin dalam banyak persekitaran perniagaan yang kompetitif.
- Tidak mengendahkan faktor kualiti, seperti perubahan selera dan fesyen.
Percepatan urutan
Kaedah ekstrapolasi adalah untuk mewujudkan garis tangen pada akhir data yang diketahui dan mengembangkannya di luar kawasan ini. Seperti halnya interpolasi, ekstrapolasi menggunakan banyak kaedah yang memerlukan pengetahuan terlebih dahulu tentang proses yang mewujudkan titik data yang ada. Kaedah ini merangkumi ekstrapolasi linear dan polinomial, conics dan ekstrapolasi lengkung Perancis.
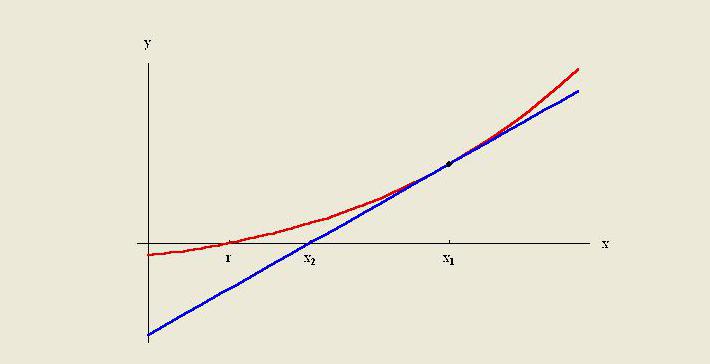
Sebagai peraturan, kualiti kaedah tertentu dihadkan oleh andaian mengenai fungsi tersebut. Dalam analisis berangka, ekstrapolasi Richardson adalah kaedah pecutan urutan yang digunakan untuk meningkatkan kadar penumpuan.Ia dinamakan selepas Lewis Fry Richardson. Beliau memperkenalkan teknik pengiraan pada permulaan abad ke-20, kegunaannya untuk pengiraan praktikal tidak dapat dipandang remeh.
Aplikasi praktik dari ekstrapolasi Richardson termasuk integrasi Romberg, yang menerapkannya pada aturan trapezoid dan algoritma Bulliers-Stoehr untuk menyelesaikan persamaan diferensial biasa.
Kaedah linear
Kaedah ekstrapolasi linear berguna apabila fungsi linear ditentukan. Ini dilakukan dengan melukis garis tangen di titik akhir graf yang diberikan dan memperluaskannya. Kaedah ekstrapolasi dalam peramalan memberikan hasil yang baik apabila titik yang diramalkan tidak terlalu jauh dari data. Interpolasi linear berguna dalam mencari nilai antara titik yang diberikan. Ia boleh dianggap sebagai "mengisi jurang" jadual data.
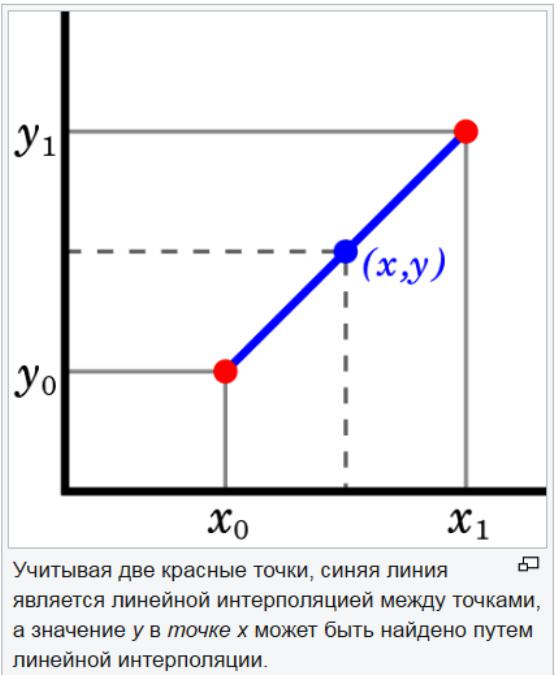
Strategi interpolasi linear adalah menggunakan garis lurus untuk menghubungkan titik nilai yang diketahui di kedua-dua belah pihak yang tidak diketahui. Interpolasi linear tidak tepat untuk parameter bukan linear. Sekiranya titik-titik dalam set data berubah dengan jumlah yang besar, interpolasi linear mungkin memberikan anggaran yang salah.
Ekstrapolasi linear dapat membantu menganggarkan nilai yang lebih tinggi atau lebih rendah daripada nilai-nilai dalam set data. Strateginya adalah menggunakan subset data dan bukan keseluruhan set. Untuk jenis nilai ini, adalah berguna untuk menggunakan kaedah ekstrapolasi dalam peramalan menggunakan dua atau tiga mata terakhir untuk menganggarkan nilai yang melebihi julat data.
Ekstrapolasi polinomial dan kon
Adalah diketahui bahawa tiga mata memberikan polinomial yang unik. Keluk polinomial boleh diteruskan selepas akhir data sedemikian. Biasanya ia dijalankan oleh kaedah Newton dengan perbezaan terhingga atau menggunakan formula interpolasi Lagrange. Polinomial pesanan yang lebih tinggi harus diekstrapolasi dengan penjagaan yang sewajarnya, kerana terdapat kemungkinan kesilapan yang adil dengan ekstrapolasi polinom. Jika ini berlaku, anggaran ralat akan meningkat secara eksponen dengan tahap polinomial.
Dalam matematik, ekstrapolasi polinomial minimum ialah transformasi urutan yang digunakan untuk mempercepat penumpuan. Walaupun kaedah Aitken paling terkenal, ia sering gagal, terutama untuk urutan vektor. Dalam kes ini, lelaran dilakukan yang membina matriks. Lajurnya adalah perbezaan.

Sebagai contoh, kaedah ekstrapolasi untuk seksyen kerucut boleh dibuat menggunakan 5 mata yang ditunjukkan berhampiran akhir data. Sekiranya bahagian kerong adalah bulatan atau elips, maka ia akan berbalik dan bersatu kembali dengan sendirinya. Parabola atau hiperbola tidak pernah bersilang. Tetapi mereka boleh membongkok paksi X. Ekstrapolasi kon dapat dilakukan di atas kertas dengan seksyen kerucut atau menggunakan komputer.
Kaedah Penilaian Matematik
Dalam kaedah ekstrapolasi ini, nilai bagi tempoh asas diramalkan. Tindakan yang diterangkan di bawah ini dilakukan secara automatik oleh sistem dan tidak dapat dilihat oleh pengguna. Keterangan dimaksudkan untuk memperbaiki algoritma, yang memaparkan nilai-nilai yang diharapkan dari jumlah yang disimpan dalam sistem, dan meramalkan hasil pengukuran meter.
Ekstrapolasi menggunakan takrifan jumlah prosedur dilakukan dengan menggunakan fungsi: Yt = f (yi, t, aj).
Sebagai asas untuk ekstrapolasi, data bulat tempoh asas tipikal yang disimpan dalam hasil bacaan ditambah. Sistem menentukan berat Yt data siri masa dalam t (masa tempoh ramalan) untuk mendapatkan penyelesaian yang betul dengan ekstrapolasi. Di mana pada titik rujukan diambil yi - tahap siri dan parameter - parameter persamaan trend.
Ramalan Ciri
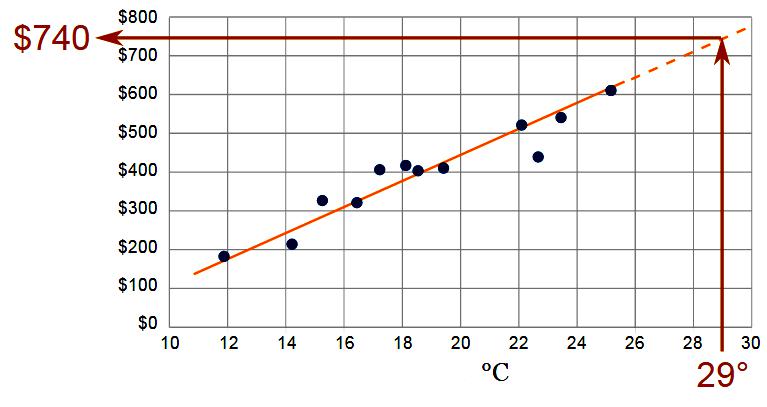
Kaedah penetapan lengkung statistik boleh digunakan untuk meramalkan fungsi.Prosedur statistik sepadan dengan data lepas satu atau lebih fungsi matematik, seperti linear, logaritma, Fourier, atau eksponen. Yang terbaik dipilih oleh ujian statistik. Kemudian ramalan ini diekstrapolasi dari sambungan matematik ini dengan kaedah ekstrapolasi matematik. Salah satu cara termudah untuk mendapatkan anggaran kasar masa depan (atau masa lalu) ialah untuk mengekstrapolasi data yang berubah dari masa ke masa.
Contohnya, jika anda perlu membuat penilaian kasar paras pencemaran di masa depan dalam air minum selama 20 tahun lebih awal, anda boleh mengekspresikan trend ini sejak 20 tahun yang lalu. Perkara yang sama diperhatikan sekiranya anda perlu menganggarkan kanser merokok atau kanser paru-paru di latar belakang pada masa akan datang. Ramalan boleh dibuat dengan mengira trend sejak beberapa tahun kebelakangan ini. Penyusutan jenis ini boleh dilakukan dengan menggunakan kaedah yang kurang kompleks. Dalam banyak kes (terutamanya dalam bidang pemasaran dan pengurusan perniagaan), kaedah ekstrapolasi secara tradisional digunakan, contohnya, dengan melihat data terkini dan secara intuitif menilai apa yang dimaksudkan di masa depan.
Kaedah berasaskan peraturan juga boleh digunakan dengan menggunakan satu set prinsip atau harapan yang telah ditetapkan berdasarkan pemahaman awal mengenai sistem dan mengambil kira data terkini untuk menafsirkan peristiwa masa depan.
Dengan kaedah ekstrapolasi, kewaspadaan adalah penting kerana terdapat banyak ketidakpastian. Prosedur ekstrapolasi mana-mana berdasarkan kepada andaian bahawa maklumat yang boleh dipercayai tersedia dalam data dan pengetahuan yang lepas. Oleh itu, masa depan ditentukan oleh faktor yang sama yang berlaku sebelum ini.
Kesilapan Peramalan
Kesalahan ekstrapolasi (lebih tepatnya, kesilapan ekstrapolasi yang tidak wajar) berlaku apabila fenomena yang bertanggungjawab untuk beberapa kesan tempatan remeh dibaca sebagai fenomena global yang hebat. Satu lagi sebab untuk kesilapan ialah kadang-kadang peraturan umum disimpulkan dari terlalu sedikit fakta. Oleh itu, teori evolusi Darwin adalah contoh hebat penerapan kaedah ekstrapolasi, di mana mekanisme perubahan rawak dan pemilihan semula jadi diumumkan untuk mengambil kira perkembangan struktur kompleks seperti penglihatan mamalia atau sistem imun organisma hidup.
Apabila cuba menafsirkan hasil penyelidikan, ahli sains harus mengelakkan ekstrapolasi di luar julat data dan sedar tentang andaian asas untuk mengelakkan menerima kesimpulan yang tidak sah. Secara umum, ekstrapolasi adalah alat saintifik yang sah. Terdapat dua aspek yang membantu membezakan antara ekstrapolasi yang sah dan salah. Kebarangkalian penyimpulan kesalahan adalah lebih tinggi apabila titik untuk data yang tidak mencukupi diperolehi untuk pembinaannya.
Alat Statistik Excel
Untuk mencari korelasi antara tahun dan hasil (contohnya, dalam perniagaan), anda boleh menggunakan Excel.
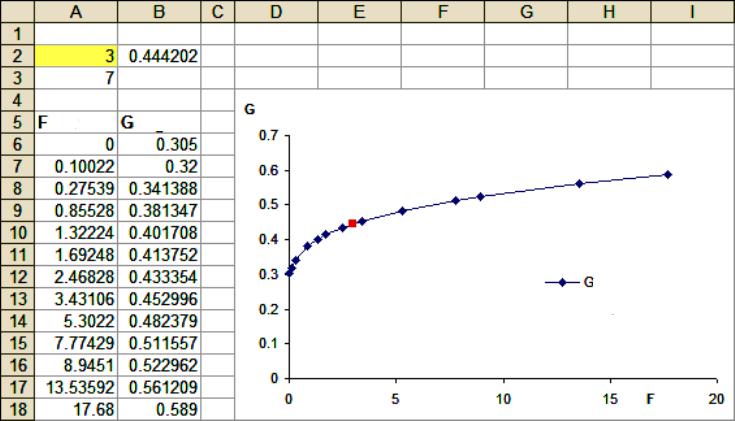
Untuk tugas ini, alat statistik untuk pemodelan ekstrapolasi digunakan yang dibina dalam semua versi Excel, bermula dengan 97. Prosedur:
- Masukkan nilai yang diketahui, sebagai contoh, jumlah jualan untuk 2016-2017, jika anda perlu menentukannya untuk tahun 2018 dan 2020.
- Pasang Analisis, ciri yang memerlukan penggunaan tambahan.
- Untuk memasangnya, ekstrak dari menu "Tools", "Add-ons".
- Semak tetingkap utiliti analisis dan sahkan dengan "OK".
- Ukur korelasi antara dua siri.
- Ekstrapolasi yang perlu dilakukan hanya masuk akal jika terdapat trend yang jelas (korelasi) di antara kedua-dua set nombor (tahun dan jualan) dengan kaedah trend ekstrapolasi.
- Untuk mengukur korelasi ini, gunakan menu "Alat", "Analisis Utiliti".
- Dalam senarai "Alat Analisis" pilih "Analisis Korelasi" dan klik "OK".
- Dalam medan Input Range masukkan julat dianalisis, sebagai contoh A6: B18, Excel akan menambah simbol "$".
- Di kawasan "Output Options", periksa julat output dan masukkannya di medan bersebelahan.
- Sahkan dengan OK.
- Excel mencipta pelbagai dua baris dalam dua lajur. Cari nilai yang dikira (contohnya, 0.981). Oleh kerana nilai ini hampir kepada 1, ini bermakna terdapat korelasi yang kukuh antara tahun dan angka jualan. Sekiranya pengguna menerima nilai yang hampir kepada sifar, ini bermakna bahawa trend tidak berlaku. Dalam kes ini, ekstrapolasi tidak masuk akal.
- Penilaian nilai masa hadapan bermula.
- Pilih julat yang diperlukan dan klik butang "Carta Wizard".
- Pilih carta (contohnya, titik awan) dan klik Selesai.
Penggunaan purata bergerak
Kedua kaedah ekstrapolasi ini melibatkan penggunaan data jualan yang meluas untuk meramal masa depan. Nilai purata bergerak mengambil satu siri data dan "turunkan" turun naik di dalamnya. Matlamatnya ialah mengekstrak extrema data dari tempoh ke semasa. Pergerakan purata sering dikira setiap suku tahun atau mingguan. Untuk meramalkan nilai masa depan, ekstrapolasi melibatkan penggunaan trend yang ditubuhkan oleh data sejarah. Anggapan utama ekstrapolasi ialah sampel akan diteruskan pada masa akan datang, kecuali jika bukti sebenar menunjukkan sebaliknya. Untuk memahami kaedah ini dengan lebih terperinci, anda boleh mempertimbangkan carta yang menunjukkan jualan alat untuk perniagaan besar dari tahun 2012 hingga 2015.
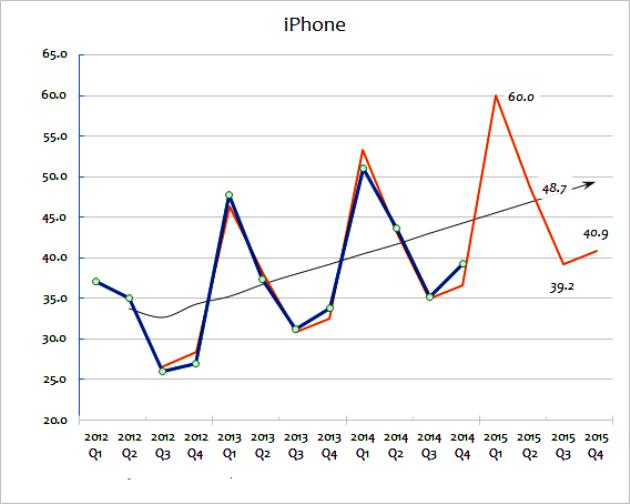
Kaedah ekstrapolasi ini menunjukkan angka jualan sebenar. Seperti yang dapat anda lihat, jumlah jualan berbeza dari tahun ke tahun, walaupun anda boleh meneka (melihat data) yang terdapat trend umum untuk pertumbuhan jualan. Baris hitam menunjukkan purata bergerak. Ini dikira dengan menambah tahun jualan yang lalu (mis. Q1 + Q2 + Q3 + Q4) dan kemudian dibahagikan dengan empat.
Kaedah ini melancarkan perubahan tahunan dan memberikan idea yang baik tentang trend umum dalam jualan tahunan. Purata bergerak membantu menunjukkan trend pertumbuhan, dinyatakan sebagai peratusan. Ia adalah ekstrapolasi ini yang akan digunakan terlebih dahulu untuk meramalkan laluan jualan masa depan. Ini boleh dilakukan secara matematik menggunakan spreadsheet. Sebagai alternatif, trend yang diekstrapolasi hanya dapat ditarik pada carta sebagai anggaran kasar.
Hubungan korelasi
Sentiasa satu teknologi adalah pelopor yang lain. Ini berlaku apabila kemajuan yang dibuat dalam teknologi pendahulunya boleh diterima pakai oleh teknologi pengikut. Apabila wujud perhubungan sedemikian, pengetahuan mengenai perubahan dalam teknologi pendahulu boleh digunakan untuk meramalkan kemajuan teknologi pengikut pada masa akan datang. Di samping itu, ekstrapolasi pendahulunya membolehkan meramalkan kesinambungan tindak balas di luar kelewatan masa.
Dalam kes ini, kaedah ekstrapolasi trend digunakan, di mana, sebagai contoh, trend dalam kelajuan pesawat ketenteraan dan pengangkutan dibandingkan. Satu lagi contoh ramalan korelasi trend ialah meramalkan saiz dan kekuatan komputer masa hadapan berdasarkan kemajuan dalam teknologi mikroelektronik. Kadang-kadang teknologi pengikut bergantung pada beberapa teknologi prekursor, tetapi bukan pada satu pendahulunya.
Gabungan gabungan pendahulu boleh mempengaruhi perubahan urutan, tetapi lebih kerap kombinasi tidak tetap, dan masukan dari pendahulunya berbeza dalam gabungan dan kekuatan. Sebagai contoh, peningkatan dalam kelajuan pesawat boleh berlaku disebabkan peningkatan enjin, bahan, kawalan, bahan bakar, aerodinamik dan pelbagai kombinasi faktor-faktor ini.
Contoh ramalan korelasi yang diperolehi dengan trend ekstrapolasi: jumlah km penumpang, jumlah kilometer geografi, dan purata kuasa pendaratan.Ekstrapolasi trend yang ditentukan secara statistik membolehkan pendekatan objektif untuk meramalkan. Walau bagaimanapun, pendekatan ini mempunyai batasan dan perangkap yang serius. Sebarang kesilapan atau pilihan tidak betul yang dibuat dalam penentuan data sejarah akan ditunjukkan dalam ramalan, yang mengurangkan nilainya.
Aplikasi, Atribut dan Had
Kaedah ekstrapolasi dimiliki oleh bidang ramalan. Beliau mencadangkan bahawa corak yang wujud pada masa lalu akan terus ke masa depan, dan corak ini adalah tetap dan boleh diukur. Dengan kata lain, masa lalu adalah penunjuk yang baik masa depan. Aplikasi berguna untuk membangunkan data asas.
Atribut dan had adalah alat pengiraan yang mudah dan murah, serta model teoretikal yang kompleks.
- Memproses data - graf dan pemerhatian.
- Kuncinya mempunyai pangkalan data yang baik dan memahami struktur di dalamnya.
- Teknik adalah tahap terbaik, nisbah dan sebagainya.
Prosedur statistik piawai sementara tidak membawa kepada pemilihan trend yang tepat yang boleh ditakluki para peramal dengan selesa, melaksanakan ramalan dengan ekstrapolasi. Dalam kes sedemikian, peramal boleh "menyesuaikan" keputusan statistik menggunakan penghakiman. Ia juga boleh mengabaikan perangkaan sepenuhnya dan mengamalkan keseluruhan trend berdasarkan penghakiman.
Ramalan yang dihasilkan dengan cara ini kurang tepat berbanding ramalan statistik, tetapi tidak semestinya tidak memuaskan. Salah satu contoh mengenai penyusunan semula trend kualiti adalah meramal kerumitan pesawat. Percubaan untuk mengukur trend ini tidak berjaya. Tetapi peratusan bahagian bergerak atau laras pesawat itu diekstrapolasi dengan kekerapan yang mana elemen tersebut diperkenalkan pada masa lalu. Ramalan ini agak tepat.
Perubahan teknikal khusus tidak boleh diramalkan dengan cara ini, tetapi tahap perubahan boleh. Ini menyediakan bahan-bahan perancangan yang berguna, menunjukkan trend dalam tingkah laku lalu.
