Saliktais vārds "ekstrapolācija" sastāv no diviem vienkāršiem vārdiem. Pirmais latīņu valodā izklausās papildus un nozīmē “ārpus”, “par”, “ārpus”. Otrais tajā pašā latīņu valodā skan polire un nozīmē “mainīt”, “iztaisnot”, “izlīdzināt”. Parasti ekstrapolāciju var definēt kā vērtību, kas atrodas ārpus diviem dotajiem punktiem. Tiek uzskatīts novērtējums tam, kas iegūts no zināmiem faktiem, kas paplašina datus nezināmā apgabalā, lai sasniegtu paredzēto rezultātu. Šo koncepciju var attiecināt arī uz nākotnes tēla prognozēšanu, pieņemot pašreizējo un pagātnes tendenču patiesumu.
Ekstrapolācijas metode paredz, ka dati vai novērojumi arī turpmāk būs līdzīgi. Tādējādi var paredzēt nākotnes rezultātus. To var uzskatīt par matemātisku hipotēzi. Ekstrapolācijā tiek izmantoti dati un fakti par konkrētu situāciju un tiek sniegtas prognozes par to, kas var notikt beigās.
Ekstrapolācijas vēsture

Šo metodi bieži sauc par Ričardsona ekstrapolāciju vai Romberga metodi. Bet tas nav pilnīgi pareizi, jo gadsimtiem ilgi ir bijušas līdzīgas skaitliskās metodes šādu problēmu risināšanai. Tāpēc slavenais Richardson h2 (ekstrapolācija skaitliskam risinājumam) nav pirmais. Līdzīga metode bija piemērojama Huygens aprēķinos jau 1654. gadā. Pats termins "ekstrapolācija" pirmo reizi tika izveidots Tomass D. Klērsons 1959. gadā grāmatā par zinātni un fantastiku.
Ekstrapolācijas metodes var saprast kā datu vai procesu paplašināšanu, kas liek domāt, ka līdzīgs process tiks piemērots arī ārpus tiem. Ekstrapolācija ir svarīgs jēdziens, ko izmanto ne tikai matemātikā, bet arī citās jomās, piemēram, socioloģijā, psiholoģijā, prognozēšanā. Piemēram, autovadītājs parasti ekstrapolē braukšanas apstākļus ārpus redzesloka. Ekstrapolāciju var attiecināt uz metodi, kurā datu vērtības tiek traktētas kā punkti x1, x2 ..., xn, un pēc tam vērtība tuvojas noteiktā punktu diapazona robežai.
Lietošanas priekšrocības:
- Vienkārša prognozēšanas metode.
- Nav nepieciešams daudz datu.
- Ātra un lēta analītika.
Metode pastāv statistikā. Ja periodiski tiek noņemtas kādas vērtības, atbilde tuvojas nākamajam datu punktam. Ekstrapolācijas metodes piemērs ir laika prognoze, kas pēta datu fona un ekstrapolē paredzamo nākotnes modeli. Vēl vienkāršāks piemērs, ja jums ir informācija par svētdienām, pirmdienām un otrdienām, varat ekstrapolēt trešdienu vai ceturtdienu.
Ekstrapolācijas izmantošanas trūkumi:
- Neuzticamība, ja ir būtiskas vēsturisko datu svārstības.
- Pieņēmums, ka pagātnes tendence saglabāsies arī nākotnē, daudzās konkurences uzņēmējdarbības vidēs diez vai ir iespējams.
- Tiek ignorēti kvalitātes faktori, piemēram, gaumes un modes izmaiņas.
Secības paātrinājums
Ekstrapolācijas metodes ir zināmu datu beigās izveidot pieskares līniju un paplašināt to ārpus šīs zonas. Tāpat kā interpolācija, ekstrapolācijā tiek izmantotas daudzas metodes, kurām ir vajadzīgas iepriekšējas zināšanas par procesu, kas veido esošos datu punktus. Metode ietver lineāro un polinomu ekstrapolāciju, koniskos un franču līknes ekstrapolāciju.
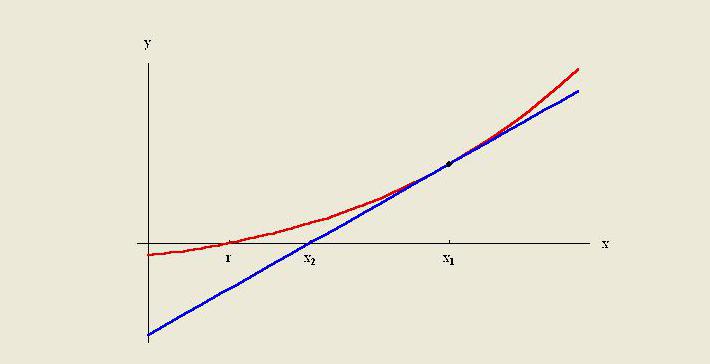
Parasti noteiktas metodes kvalitāti ierobežo pieņēmumi par funkciju. Skaitliskajā analīzē Ričardsona ekstrapolācija ir kārtas paātrināšanas metode, ko izmanto, lai uzlabotu konverģences ātrumu.Tas ir nosaukts pēc Lūisa Frī Ričardsona. Viņš 20. gadsimta sākumā ieviesa aprēķināšanas paņēmienu, kura praktisko aprēķinu lietderību diez vai var pārvērtēt.
Richardsona ekstrapolācijas praktiskie pielietojumi ietver Romberga integrāciju, kas to piemēro trapecveida likumam un Bulliers-Stoehr algoritmam parasto diferenciālvienādojumu risināšanai.
Lineārā metode
Lineārās ekstrapolācijas metode ir noderīga, ja ir norādīta lineārā funkcija. Tas tiek izdarīts, novilkot pieskares līniju dotā grafika beigu punktā un paplašinot to ārpus. Šī ekstrapolācijas metode prognozēšanā dod labus rezultātus, ja prognozējamais punkts nav pārāk tālu no datiem. Lineārā interpolācija ir noderīga, lai atrastu vērtības starp dotajiem punktiem. To var uzskatīt par datu tabulas "nepilnību aizpildīšanu".
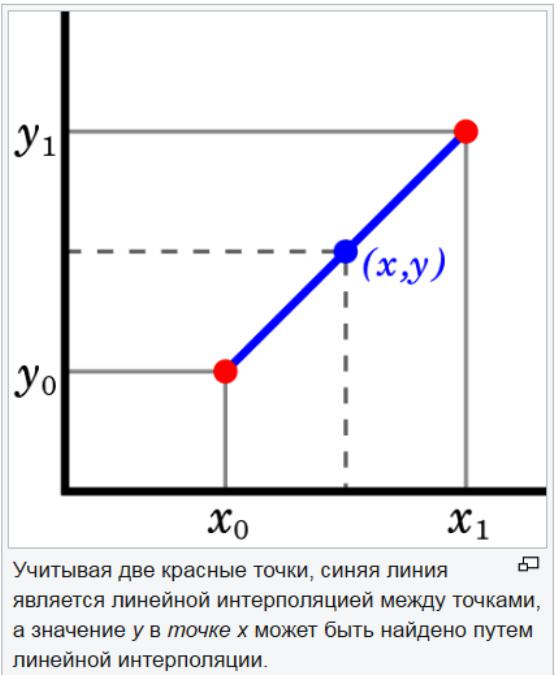
Lineārā interpolācijas stratēģija ir izmantot taisnu līniju, lai savienotu zināmos vērtību punktus abpus nezināmajam. Lineārā interpolācija nav precīza nelineāriem parametriem. Ja punkti datu kopā mainās par lielu daudzumu, lineārā interpolācija var sniegt nepareizu aprēķinu.
Lineārā ekstrapolācija var palīdzēt novērtēt vērtības, kas ir augstākas vai zemākas par vērtībām datu kopā. Tās stratēģija ir izmantot datu apakškopu, nevis visu komplektu. Šāda veida vērtībai ir lietderīgi izmantot ekstrapolācijas metodi prognozēšanai, izmantojot pēdējos divus vai trīs punktus, lai novērtētu vērtību, kas pārsniedz datu diapazonu.
Polinomu un konisko ekstrapolāciju
Ir zināms, ka trīs punkti dod unikālu polinomu. Polinomu līkni var turpināt pēc šādu datu beigām. To parasti veic ar Ņūtona metodi ar ierobežotu starpību vai izmantojot Lagranža interpolācijas formulu. Augstākas kārtas polinoms būtu ekstrapolējams ar pienācīgu rūpību, jo pastāv daudz izredžu kļūdas, izmantojot polinomu ekstrapolāciju. Ja tas notiek, kļūdas novērtējums palielināsies eksponenciāli līdz ar polinoma pakāpi.
Matemātikā minimāla polinomu ekstrapolācija ir sekvences transformācija, ko izmanto, lai paātrinātu konverģenci. Lai arī Aitkena metode ir vislabāk zināma, tā bieži neizdodas, īpaši vektoru sekvencēm. Šajā gadījumā tiek veikta iterācija, kas izveido matricu. Tās kolonnas ir atšķirības.

Piemēram, konsoles sekcijas ekstrapolācijas metodi var veikt, izmantojot 5 punktus, kas norādīti tuvu datu beigām. Ja koniskais sekcija ir aplis vai elipse, tad tā atgriezīsies un atkal apvienosies ar sevi. Parabola vai hiperbola nekad nekrustojas. Bet tos var noliekt atpakaļ ap X asi.Konusa ekstrapolāciju var veikt uz papīra ar konisku sekciju vai izmantojot datoru.
Matemātiskās vērtēšanas metode
Šajā ekstrapolācijas metodē tiek prognozēta bāzes perioda vērtība. Tālāk aprakstītās darbības sistēma automātiski veic, un lietotājs tās neredz. Apraksts ir paredzēts, lai precizētu algoritmu, kas parāda gaidāmās vērtības no sistēmā saglabātā daudzuma un prognozē skaitītāja mērīšanas rezultātu.
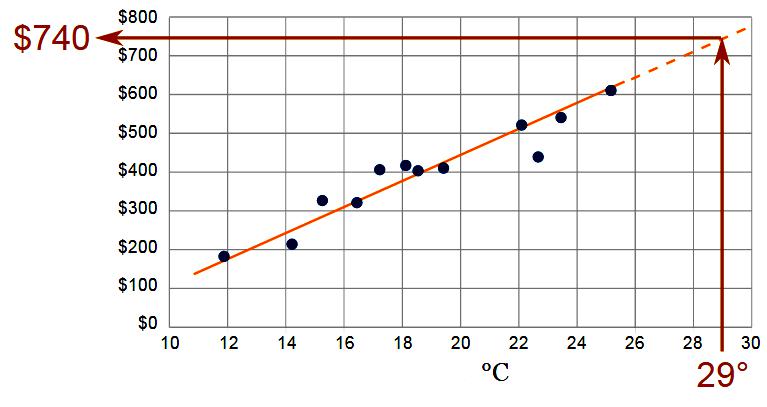
Ekstrapolācija, izmantojot procedūras apjoma definīciju, tiek veikta, izmantojot funkciju: Yt = f (yi, t, aj).
Kā pamats ekstrapolācijai tiek pievienoti nolasītie tipiskā bāzes perioda dati, kas saglabāti nolasīšanas rezultātos. Sistēma nosaka laika rindu datu svaru Yt t (prognozētā perioda laiks), lai ekstrapolējot iegūtu pareizo risinājumu. Kur atskaites punktā ņem yi - sērijas līmeni un aj - tendences vienādojuma parametru.
Feature Prognoze
Statistiskās līknes fiksēšanas metode ir piemērojama funkcionalitātes prognozēšanai.Statistiskās procedūras atbilst pagātnes datiem par vienu vai vairākām matemātiskām funkcijām, piemēram, lineārajai, logaritmiskajai, Furjē vai eksponenciālajai. Labākos izvēlas ar statistisko testu. Tad šī prognoze tiek ekstrapolēta no šī matemātiskā savienojuma ar matemātiskās ekstrapolācijas metodi. Viens no vienkāršākajiem veidiem, kā iegūt aptuvenus nākotnes (vai pagātnes) apstākļu novērtējumus, ir ekstrapolēt datus, kas laika gaitā mainās.
Piemēram, ja jums ir nepieciešams aptuveni 20 gadus iepriekš aptuveni novērtēt piesārņojošo vielu līmeni dzeramajā ūdenī, varat ekstrapolēt šo tendenci no pēdējiem 20 gadiem. Tas pats tiek novērots, ja nākotnē jums ir jānovērtē smēķēšanas vai plaušu vēža izplatība fona. Prognozi var veikt, aprēķinot pēdējo gadu tendences. Šāda veida ekstrapolācijas var veikt, izmantojot mazāk sarežģītas metodes. Daudzos gadījumos (īpaši mārketinga un biznesa vadības jomā) tradicionāli tiek izmantota ekstrapolācijas metode, piemēram, apskatot jaunākos datus un intuitīvi novērtējot, kas domāts nākotnē.
Uz noteikumiem balstītas metodes var izmantot arī, piemērojot iepriekš noteiktu principu vai cerību kopumu, kas balstās uz iepriekšēju sistēmas izpratni un, ņemot vērā jaunākos datus, lai interpretētu turpmākos notikumus.
Izmantojot jebkuru ekstrapolācijas metodi, svarīga ir piesardzība, jo pastāv daudz neskaidrību. Jebkura ekstrapolācijas procedūra balstās uz pieņēmumu, ka pagātnes datos un zināšanās ir pieejama uzticama informācija. Līdz ar to nākotni nosaka tie paši faktori, kas rīkojās iepriekš.
Prognozēšanas kļūdas
Ekstrapolācijas kļūda (precīzāk - nepamatotas ekstrapolācijas kļūda) rodas, kad parādība, kas atbildīga par vairākiem triviāliem vietējiem efektiem, tiek lasīta kā lielas globālas parādības. Vēl viens kļūdas iemesls ir tas, ka dažreiz vispārinātus noteikumus izsecina no pārāk maz faktu. Tādējādi Dārvina evolūcijas teorija ir fantastisks ekstrapolācijas metodes pielietojuma piemērs, kurā tiek paziņoti nejaušu izmaiņu un dabiskās atlases mehānismi, lai ņemtu vērā tādu sarežģītu struktūru attīstību kā zīdītāju redze vai dzīvo organismu imūnsistēma.
Mēģinot interpretēt pētījumu rezultātus, zinātniekam jāizvairās no ekstrapolācijas ārpus datu diapazona un jāapzinās pamatā esošie pieņēmumi, lai izvairītos no kļūdainu secinājumu pieņemšanas. Parasti ekstrapolācija ir likumīgs zinātnisks līdzeklis. Ir divi aspekti, kas palīdz atšķirt derīgu un kļūdainu ekstrapolāciju. Kļūdainas ekstrapolācijas varbūtība ir augstāka, ja par tās uzbūvi tika iegūti punkti par nepietiekamiem datiem.
Excel statistikas rīki
Lai atrastu korelāciju starp gadiem un rezultātiem (piemēram, biznesā), varat izmantot programmu Excel.
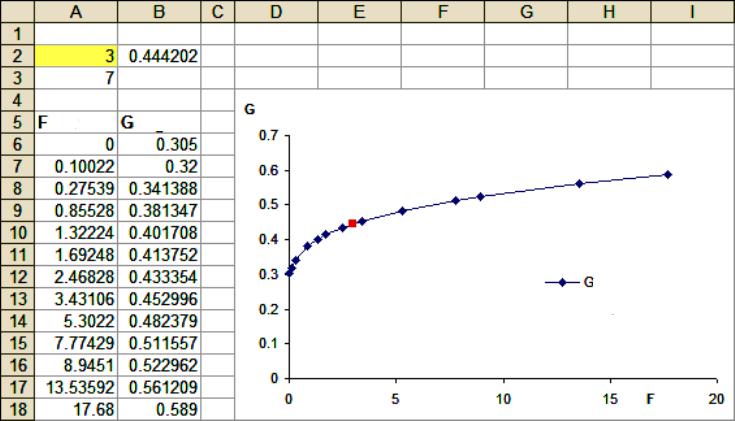
Šiem uzdevumiem tiek izmantoti statistikas rīki ekstrapolācijas modelēšanai, kas ir iebūvēti visās Excel versijās, sākot ar 97. Procedūra:
- Ievadiet zināmās vērtības, piemēram, kopējo pārdošanas apjomu 2016. – 2017. Gadam, ja jums tās ir jānosaka 2018. un 2020. gadam.
- Instalēt analīzi - funkciju, kurai nepieciešams izmantot pievienojumprogrammu.
- Lai to instalētu, izvelciet no izvēlnes “Rīki”, “Papildinājumi”.
- Pārbaudiet analīzes utilītas logu un apstipriniet ar “OK”.
- Izmēriet korelācijas starp divām sērijām.
- Ekstrapolācijai, kas jāveic, ir jēga tikai tad, ja starp abām skaitļu kopām (gadiem un pārdošanas apjomiem) ir skaidra tendence (korelācija) ar tendenču ekstrapolācijas metodi.
- Lai izmērītu šo korelāciju, izmantojiet izvēlni “Tools”, “Analysis Utilities”.
- Sarakstā “Analīzes rīki” atlasiet “Korelācijas analīze” un noklikšķiniet uz “Labi”.
- Laukā Input Range ievadiet analizēto diapazonu, piemēram, A6: B18, Excel pievienos simbolu "$".
- Apgabalā "Output Options" pārbaudiet izvades diapazonu un ievadiet to blakus esošajā laukā.
- Apstipriniet ar Labi.
- Excel izveido masīvu no divām rindām divās kolonnās. Atrodiet aprēķināto vērtību (piemēram, 0,981). Tā kā šī vērtība ir tuvu 1, tas nozīmē, ka starp gadiem un pārdošanas rādītājiem pastāv cieša korelācija. Ja lietotājs saņem vērtību, kas ir tuvu nullei, tas nozīmē, ka tendence nenotiek. Šajā gadījumā ekstrapolācijai nav jēgas.
- Sākas nākotnes vērtību novērtēšana.
- Atlasiet vajadzīgo diapazonu un noklikšķiniet uz pogas "Diagrammas vednis".
- Atlasiet diagrammu (piemēram, punktu mākoņus) un noklikšķiniet uz Pabeigt.
Kustīgo vidējo vērtību izmantošana
Šīs divas ekstrapolācijas metodes paredz plašu pārdošanas datu izmantošanu nākotnes prognozēšanai. Mainīgā vidējā vērtība ņem virkni datu un “izlīdzina” to svārstības. Mērķis ir iegūt datus no viena perioda uz otru. Mainīgos vidējos rādītājus bieži aprēķina ceturksnī vai nedēļā. Lai prognozētu nākotnes vērtības, ekstrapolācija ietver tendenču izmantošanu, ko nosaka vēsturiskie dati. Ekstrapolācijas galvenais pieņēmums ir tāds, ka izlase turpinās darboties arī nākotnē, ja vien faktiskie pierādījumi neliecina par pretējo. Lai sīkāk izprastu šīs metodes, varat apsvērt diagrammu, kurā parādīti sīkrīku pārdošanas apjomi lieliem uzņēmumiem no 2012. līdz 2015. gadam.
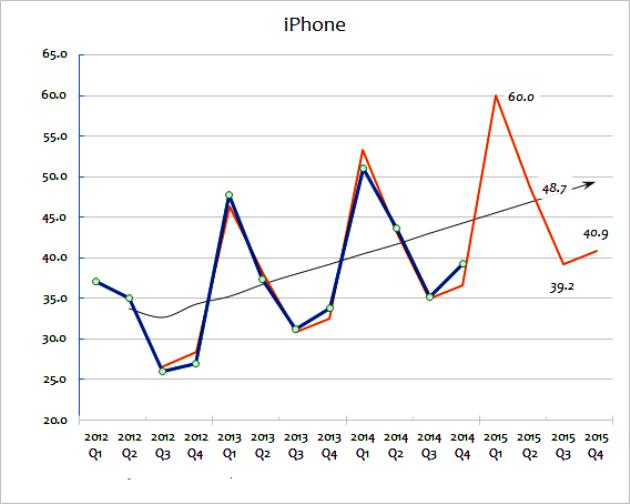
Šī aprēķina ekstrapolācijas metode parāda faktisko pārdošanas apjomu. Kā redzat, kopējais pārdošanas apjoms gadu no gada atšķiras, lai gan jūs varat uzminēt (apskatot datus), ka pārdošanas tendencēm ir vispārēja tendence. Melnā līnija parāda mainīgo vidējo rādītāju. To aprēķina, saskaitot pēdējos pārdošanas gadus (piemēram, Q1 + Q2 + Q3 + Q4) un pēc tam dalot ar četriem.
Šī metode izlīdzina ikgadējās izmaiņas un sniedz labu priekšstatu par gada pārdošanas vispārējo tendenci. Mainīgais lielums palīdz norādīt pieauguma tendenci, izteiktu procentos. Tieši šī ekstrapolācija vispirms tiks izmantota, lai prognozētu turpmāko pārdošanas ceļu. To var izdarīt matemātiski, izmantojot izklājlapu. Alternatīvi, ekstrapolētu tendenci diagrammā var vienkārši uzzīmēt kā aptuvenu novērtējumu.
Tendenču korelācija
Vienmēr viena tehnoloģija ir citas priekštece. Tas notiek tad, kad priekšteču tehnoloģijas sasniegumus var izmantot sekotāju tehnoloģija. Kad šādas attiecības pastāv, zināšanas par priekšgājēju tehnoloģiju izmaiņām var izmantot, lai nākotnē paredzētu tehnoloģiju sekotāju progresu. Turklāt prekursora ekstrapolācija ļauj paredzēt turpinājumu turpinājumu pēc laika aizkavēšanās.
Šajā gadījumā tiek izmantota tendenču ekstrapolācijas metode, kurā, piemēram, tiek salīdzinātas militāro un transporta lidmašīnu ātruma tendences. Vēl viens tendenču korelācijas prognozēšanas piemērs ir nākotnes datoru lieluma un jaudas prognozēšana, pamatojoties uz mikroelektroniskās tehnoloģijas sasniegumiem. Dažreiz sekotāju tehnoloģija ir atkarīga no vairākām prekursoru tehnoloģijām, bet ne no viena priekšgājēja.
Fiksētas priekšgājēju kombinācijas var ietekmēt secības izmaiņas, taču biežāk kombinācijas nav fiksētas, un priekšgājēju ievadi atšķiras gan kombinācijā, gan stiprumā. Piemēram, lidaparāta ātruma palielināšanās var notikt, pateicoties uzlabotiem dzinējiem, materiāliem, vadības ierīcēm, degvielai, aerodinamikai un dažādām šo faktoru kombinācijām.
Korelācijas prognozes piemērs, kas iegūts, ekstrapolējot tendences: kopējais pasažieru jūdzes, kopējais ģeogrāfiskais jūdzes un vidējā nosēšanās jauda.Statistiski noteiktu tendenču ekstrapolācija ļauj objektīvi prognozēt. Tomēr šai pieejai ir nopietni ierobežojumi un nepilnības. Visas kļūdas vai nepareiza izvēle, kas izdarīta, nosakot vēsturiskos datus, tiks atspoguļota prognozē, kas samazina tās vērtību.
Lietojumprogrammas, atribūti un ierobežojumi
Ekstrapolācijas metode ietilpst prognozēšanas jomā. Viņš norāda, ka iepriekš pastāvējušie modeļi turpināsies arī nākotnē, un ka šie modeļi ir regulāri un tos var izmērīt. Citiem vārdiem sakot, pagātne ir labs nākotnes rādītājs. Lietojumprogrammas ir noderīgas sākotnējo datu izstrādei.
Atribūti un ierobežojumi ir vienkārši un lēti aprēķināšanas rīki, kā arī sarežģīti teorētiskie modeļi.
- Procesa dati - diagrammas un novērojumi.
- Galvenais ir laba datu bāze un tās struktūras izpratne.
- Vispiemērotākā ir tehnika, attiecība un tā tālāk.
Pagaidu standarta statistikas procedūras neizraisa precīzu to tendenču izvēli, kuras prognozētājs var ekstrapolēt ar komfortu, veicot prognozi, ekstrapolējot. Šādos gadījumos prognozētājs var “pielāgot” statistikas rezultātus, izmantojot vērtējumu. Tas var arī pilnībā ignorēt statistiku un, pamatojoties uz spriedumu, ekstrapolēt visu tendenci.
Šādā veidā sagatavotas prognozes ir mazāk precīzas nekā statistiskās prognozes, taču tās nebūt nav apmierinošas. Viens no šādas kvalitātes tendences ekstrapolācijas piemēriem ir gaisa kuģa sarežģītības prognozēšana. Mēģinājumi kvantitatīvi noteikt šo tendenci nav bijuši veiksmīgi. Bet gaisa kuģa pārvietojamo vai regulējamo daļu procentuālā daļa tika ekstrapolēta ar biežumu, ar kādu šādi elementi tika ieviesti iepriekš. Šīs prognozes bija diezgan precīzas.
Konkrētas tehniskas izmaiņas šādā veidā nevar paredzēt, bet izmaiņu pakāpe to var. Tas nodrošina noderīgus plānošanas materiālus, norādot uz iepriekšējās uzvedības tendencēm.
