Sudėtinis žodis „ekstrapoliacija“ sudarytas iš dviejų paprastų žodžių. Pirmasis lotyniškai skamba papildomai ir reiškia „už“, „už“, „už“. Antrasis toje pačioje lotyniškai skamba keistai ir reiškia „pakeisti“, „ištiesinti“, „sklandžiai“. Paprastai ekstrapoliacija gali būti apibrėžta kaip reikšmė, esanti už dviejų nurodytų taškų ribų. Tai laikoma įvertinimu to, kas išgaunama iš žinomų faktų, praplečiančių duomenis nežinomoje srityje, kad būtų gautas numatytas rezultatas. Ši koncepcija taip pat gali būti priskiriama ateities įvaizdžio numatymui, darant prielaidą apie dabarties ir praeities tendencijų tiesą.
Ekstrapoliacijos metodas daro prielaidą, kad ateityje duomenys ar stebėjimai ir toliau bus panašūs. Taigi galima numatyti būsimus rezultatus. Tai galima vertinti kaip matematinę hipotezę. Ekstrapoliacija naudoja duomenis ir faktus apie konkrečią situaciją ir pateikia prognozes, kas gali nutikti pabaigoje.
Ekstrapoliacijos istorija

Šis metodas dažnai vadinamas Richardsono ekstrapoliacija arba Rombergo metodu. Bet tai nėra visiškai teisinga, nes šimtmečius buvo naudojami panašūs skaitiniai tokių problemų sprendimo būdai. Todėl garsusis Richardson h2 (ekstrapoliacija skaitmeniniam sprendimui) nėra pirmas. Panašus metodas buvo taikomas Huygenso skaičiavimams dar 1654 m. Pats terminas „ekstrapoliacija“ pirmą kartą buvo sugalvotas Thomas D. Claresono 1959 m. Mokslinėje ir fantastinėje knygoje.
Ekstrapoliacijos metodai gali būti suprantami kaip duomenų ar procesų išplėtimas, rodantys, kad panašus procesas bus taikomas ir už jų ribų. Ekstrapoliacija yra svarbi sąvoka, naudojama ne tik matematikoje, bet ir kitose srityse, tokiose kaip sociologija, psichologija, prognozavimas. Pavyzdžiui, vairuotojas paprastai ekstrapoliuoja vairavimo sąlygas už savo regėjimo ribų. Ekstrapoliacija gali būti priskirta metodui, kai duomenų vertės laikomos taškais x1, x2 ..., xn, o tada vertė artėja prie nurodyto taškų diapazono ribos.
Naudojimo privalumai:
- Paprastas prognozavimo metodas.
- Nereikia daug duomenų.
- Greita ir pigi analizė.
Metodas egzistuoja statistikoje. Jei kuri nors vertė periodiškai pašalinama, atsakymas artėja prie kito duomenų taško. Ekstrapoliacijos metodo pavyzdys yra orų prognozė, kurioje atsižvelgiama į duomenų istoriją ir ekstrapoliuojami numatomi ateities modeliai. Dar paprastesnis pavyzdys, jei turite informacijos apie sekmadienius, pirmadienius ir antradienius, galite ekstrapoliuoti trečiadienį ar ketvirtadienį.
Ekstrapoliacijos naudojimo trūkumai:
- Nepatikimumas, jei yra reikšmingų istorinių duomenų svyravimų.
- Prielaida, kad praeities tendencija išliks ir ateityje, vargu ar įmanoma daugelyje konkurencingų verslo aplinkų.
- Nepaisoma kokybės veiksnių, tokių kaip skonio ir mados pokyčiai.
Sekos pagreitis
Ekstrapoliavimo metodai yra sukurti liestinę ties žinomų duomenų gale ir išplėsti ją už šios srities ribų. Kaip ir atliekant interpoliaciją, ekstrapoliacijai naudojami daug metodų, kuriems reikia išankstinių žinių apie procesą, kuris sukuria esamus duomenų taškus. Metodas apima tiesinę ir polinominę ekstrapoliaciją, kūgines ir prancūziškojo kreivės ekstrapoliacijas.
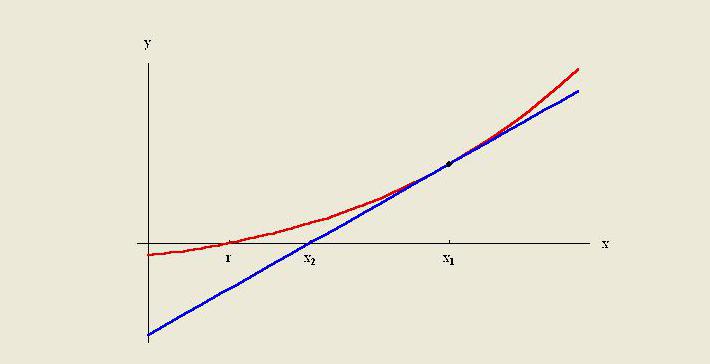
Paprastai tam tikro metodo kokybę riboja prielaidos apie funkciją. Skaitinės analizės metu Richardsono ekstrapoliacija yra sekos pagreičio metodas, naudojamas konvergencijos greičiui pagerinti.Jis pavadintas Lewiso Fry Richardsono vardu. Jis XX amžiaus pradžioje pristatė skaičiavimo techniką, kurios naudingumą atliekant praktinius skaičiavimus vargu ar galima pervertinti.
Praktiniai Richardsono ekstrapoliacijos taikymo būdai apima Rombergo integraciją, kuri ją taiko trapecijos taisyklei ir Bulliers-Stoehr algoritmui paprastoms diferencialinėms lygtims išspręsti.
Linijinis metodas
Linijinis ekstrapoliavimo metodas yra naudingas, kai nurodoma linijinė funkcija. Tai atliekama nubrėžiant liestinės liniją nurodyto grafiko galiniame taške ir išplėsdami ją už jos ribų. Šis ekstrapoliacijos metodas prognozuojant duoda gerų rezultatų, kai numatomas taškas nėra per toli nuo duomenų. Linijinė interpoliacija naudinga ieškant reikšmių tarp nurodytų taškų. Tai galima laikyti duomenų lentelės „spragų užpildymu“.
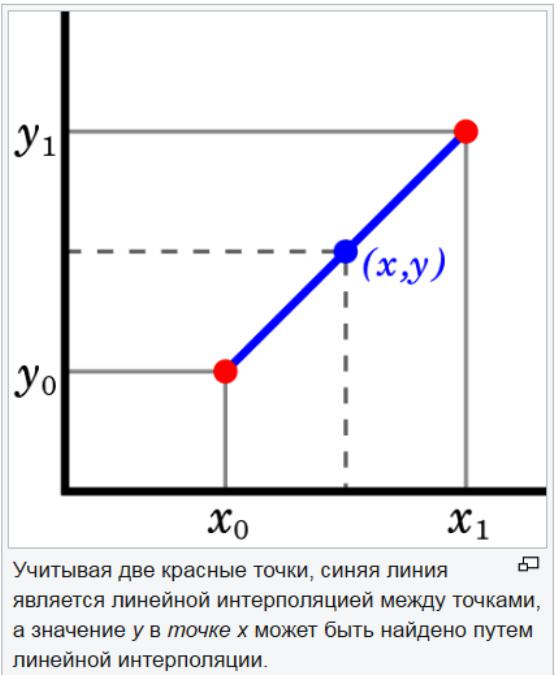
Linijinė interpoliacijos strategija yra tiesios linijos panaudojimas žinomiems vertės taškams sujungti iš abiejų nežinomų pusių. Netiesinių parametrų tiesinė interpoliacija nėra tiksli. Jei duomenų rinkinio taškai keičiasi dideliu mastu, tiesinė interpoliacija gali duoti neteisingą vertinimą.
Tiesinė ekstrapoliacija gali padėti įvertinti didesnes ar mažesnes vertes nei duomenų rinkinyje. Jos strategija yra naudoti duomenų pogrupį, o ne visą rinkinį. Tokio tipo vertėms yra naudinga taikyti ekstrapoliacijos metodą prognozuojant naudojant paskutinius du ar tris taškus, kad būtų galima įvertinti vertę, viršijančią duomenų intervalą.
Polinominė ir kūginė ekstrapoliacijos
Yra žinoma, kad trys taškai suteikia unikalią daugianarę. Pasibaigus tokiems duomenims, polinominė kreivė gali būti tęsiama. Paprastai tai atliekama Niutono metodu esant ribotam skirtumui arba naudojant Lagrange'o interpoliacijos formulę. Aukštesnės eilės polinomas turėtų būti ekstrapoliuotas deramai atsargiai, nes polinomo ekstrapoliacija turi didelę klaidų tikimybę. Jei taip atsitiks, paklaidos įvertinimas padidės eksponentiškai su polinomo laipsniu.
Matematikoje minimalus polinominis ekstrapoliavimas yra sekos transformacija, naudojama konvergencijai paspartinti. Nors Aitken metodas yra geriausiai žinomas, jis dažnai nepavyksta, ypač vektorių sekoms. Tokiu atveju atliekama iteracija, sukonstruojanti matricą. Jos stulpeliai yra skirtumai.

Pavyzdžiui, kūgio pjūvio ekstrapoliavimo metodą galima atlikti naudojant 5 taškus, nurodytus šalia duomenų galo. Jei kūgio formos pjūvis yra apskritimas ar elipsė, tada jis pasislinks atgal ir vėl susijungs. Parabolė ar hiperbolė niekada nesikerta. Jie gali būti sulenkti atgal ties X ašimi.Kolupo ekstrapoliacija gali būti atliekama ant popieriaus, naudojant kūginę dalį arba naudojant kompiuterį.
Matematinio vertinimo metodas
Šiuo ekstrapoliavimo metodu numatoma bazinio laikotarpio vertė. Žemiau aprašytus veiksmus sistema automatiškai atlieka ir vartotojui jų nematyti. Aprašymas skirtas patikslinti algoritmą, kuris rodo numatomas sistemoje saugomo kiekio vertes ir numato skaitiklio matavimo rezultatą.
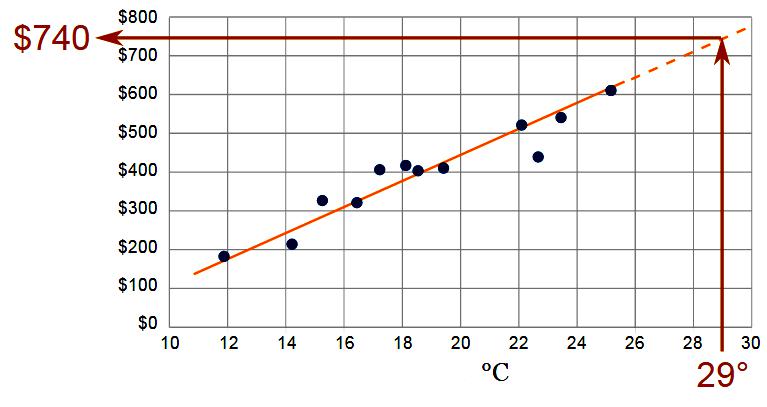
Ekstrapoliacija, apibrėžiant procedūros kiekį, atliekama naudojant funkciją: Yt = f (yi, t, aj).
Kaip ekstrapoliacijos pagrindas pridedami suapvalinti tipinio bazinio laikotarpio duomenys, saugomi skaitymo rezultatuose. Sistema nustato laiko eilučių duomenų svorį Yt (t (prognozuojamo laikotarpio laikas)), kad ekstrapoliacijos būdu gautų teisingą sprendimą. Kai atskaitos taške imamas yi - eilutės lygis ir aj - tendencijos lygties parametras.
Funkcijų numatymas
Funkcionalumui numatyti taikomas statistinės kreivės fiksavimo metodas.Statistinės procedūros atitinka praeities duomenis apie vieną ar daugiau matematinių funkcijų, tokių kaip tiesinė, logaritminė, Furjė arba eksponentinė. Geriausi išrenkami atliekant statistinį testą. Tada ši prognozė iš šio matematinio ryšio yra ekstrapoliuota matematinės ekstrapoliacijos metodu. Vienas iš paprasčiausių būdų gauti apytikslius ateities (ar praeities) sąlygų įvertinimus yra ekstrapoliuoti duomenis, kurie keičiasi laikui bėgant.
Pavyzdžiui, jei jums reikia apytiksliai įvertinti būsimą geriamojo vandens teršalų kiekį per 20 metų iš anksto, galite ekstrapoliuoti šią tendenciją iš pastarųjų 20 metų. Tas pats pastebima, jei ateityje reikia įvertinti rūkymo ar plaučių vėžio paplitimą fone. Prognozę galima sudaryti apskaičiavus pastarųjų metų tendencijas. Tokio tipo ekstrapoliacija gali būti atliekama naudojant ne tokius sudėtingus metodus. Daugeliu atvejų (ypač rinkodaros ir verslo valdymo srityse) tradiciškai naudojamas ekstrapoliacijos metodas, pavyzdžiui, peržiūrint naujausius duomenis ir intuityviai įvertinant, kas turi omenyje ateityje.
Taisyklėmis pagrįsti metodai taip pat gali būti naudojami taikant iš anksto nustatytų principų ar lūkesčių rinkinį, pagrįstą išankstiniu sistemos supratimu ir atsižvelgiant į naujausius duomenis aiškinantis būsimus įvykius.
Taikant bet kurį ekstrapoliacijos metodą, labai svarbu būti atsargiam, nes yra daugybė neaiškumų. Bet kokia ekstrapoliavimo procedūra grindžiama prielaida, kad turima patikima informacija iš ankstesnių duomenų ir žinių. Taigi ateitį lemia tie patys veiksniai, kurie veikė anksčiau.
Prognozavimo klaidos
Ekstrapoliacijos klaidingumas (tiksliau nepagrįsto ekstrapoliavimo klaidingumas) įvyksta tada, kai reiškinys, atsakingas už daugybę trivialių vietinių efektų, skaitomas kaip puikus globalus reiškinys. Kita klaidos priežastis yra ta, kad kartais bendrosios taisyklės išvedamos iš per mažai faktų. Taigi Darvino evoliucijos teorija yra puikus ekstrapoliacijos metodo taikymo pavyzdys, kuriame skelbiama, kad atsitiktinių pokyčių ir natūralios atrankos mechanizmai atsižvelgia į tokių sudėtingų struktūrų, kaip žinduolių regėjimas ar gyvųjų organizmų imuninė sistema, vystymąsi.
Bandydamas aiškinti tyrimų rezultatus, mokslininkas turėtų vengti ekstrapoliacijos už duomenų diapazono ribų ir žinoti pagrindines prielaidas, kad išvengtų klaidingų išvadų. Paprastai ekstrapoliacija yra teisėta mokslinė priemonė. Yra du aspektai, padedantys atskirti pagrįstą ir klaidingą ekstrapoliaciją. Klaidingos ekstrapoliacijos tikimybė yra didesnė, kai jos konstrukcijai gauti taškai buvo nepakankami.
„Excel“ statistiniai įrankiai
Norėdami rasti koreliaciją tarp metų ir rezultatų (pavyzdžiui, versle), galite naudoti „Excel“.
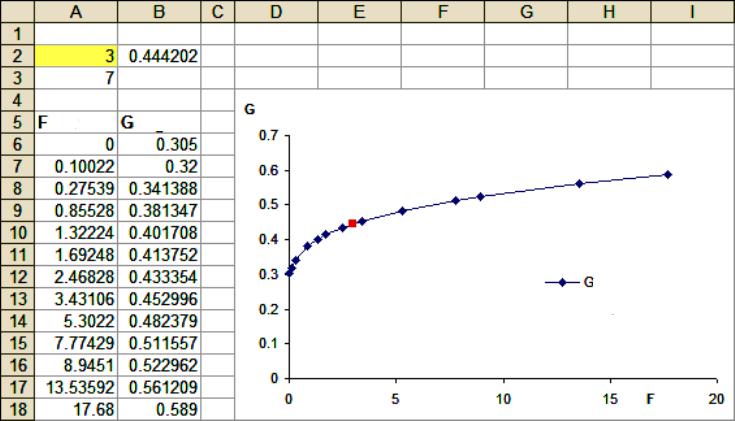
Šioms užduotims atlikti naudojami ekstrapoliavimo modeliavimo statistiniai įrankiai, integruoti į visas „Excel“ versijas, pradedant nuo 97. Procedūra:
- Įveskite žinomas vertes, pvz., Bendrą 2016–2017 m. Pardavimą, jei jums reikia jas nustatyti 2018 ir 2020 m.
- Įdiegti analizę - funkciją, kuriai reikia naudoti priedą.
- Norėdami ją įdiegti, ištraukite iš meniu „Įrankiai“, „Priedai“.
- Patikrinkite analizės paslaugų langą ir patvirtinkite „Gerai“.
- Išmatuokite dviejų serijų koreliacijas.
- Ekstrapoliacija, kurią reikia atlikti, yra prasminga tik tuo atveju, jei tarp dviejų skaičių rinkinių (metų ir pardavimo) yra aiški tendencija (koreliacija) tendencijų ekstrapoliavimo metodu.
- Norėdami išmatuoti šią koreliaciją, naudokite meniu „Įrankiai“, „Analizės priemonės“.
- Sąraše „Analizės įrankiai“ pasirinkite „Koreliacijos analizė“ ir spustelėkite „Gerai“.
- Lauke Įvesties sritis įveskite analizuojamą diapazoną, pavyzdžiui, A6: B18, „Excel“ pridės simbolį „$“.
- Srityje „Išvesties parinktys“ patikrinkite išvesties diapazoną ir įveskite jį į gretimą lauką.
- Patvirtinkite paspausdami Gerai.
- „Excel“ sukuria dviejų eilučių masyvą dviejuose stulpeliuose. Raskite apskaičiuotą vertę (pavyzdžiui, 0,981). Kadangi ši vertė yra artima 1, tai reiškia, kad yra tvirtas ryšys tarp metų ir pardavimų skaičiaus. Jei vartotojas gauna reikšmę, artimą nuliui, tai reikš, kad tendencija nepasireikš. Šiuo atveju ekstrapoliacija neturi prasmės.
- Pradedamas vertinti būsimas vertybes.
- Pasirinkite reikiamą diapazoną ir spustelėkite mygtuką „Diagramos vedlys“.
- Pasirinkite diagramą (pavyzdžiui, taškinius debesis) ir spustelėkite Baigti.
Slenkamų vidurkių naudojimas
Šie du ekstrapoliavimo metodai apima platų pardavimo duomenų naudojimą numatant ateitį. Slenkama vidutinė vertė užima daugybę duomenų ir „išlygina“ jų svyravimus. Tikslas yra išgauti duomenų ekstremumą iš vieno laikotarpio į kitą. Slenkamieji vidurkiai dažnai apskaičiuojami kas ketvirtį arba savaitę. Norint nuspėti būsimas vertes, ekstrapoliacija apima istorinių duomenų nustatytų tendencijų naudojimą. Pagrindinė ekstrapoliacijos prielaida yra ta, kad imtis bus tęsiama ir ateityje, nebent faktiniai įrodymai rodo kitaip. Norėdami išsamiau suprasti šiuos metodus, galite apsvarstyti diagramą, kurioje pateikiami įtaisų pardavimai didelėms įmonėms nuo 2012 iki 2015 m.
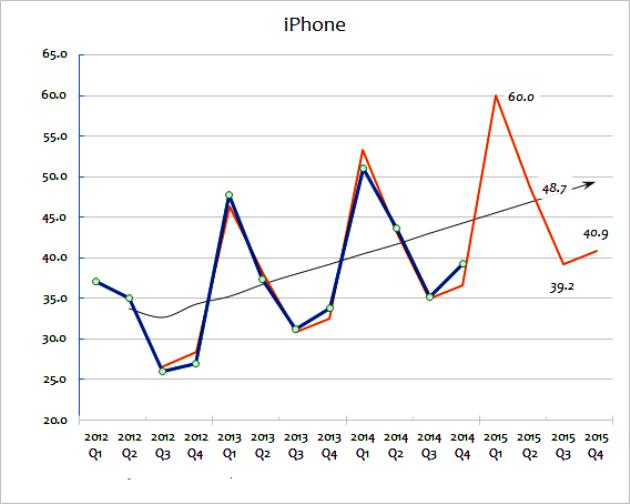
Šis skaičiavimo ekstrapoliavimo metodas parodo tikrąjį pardavimų skaičių. Kaip matote, bendra pardavimų suma kiekvienais metais skiriasi, nors galite spėti (žiūrėdami į duomenis), kad yra bendra pardavimų augimo tendencija. Juodoji linija rodo slenkamąjį vidurkį. Tai apskaičiuojama sudedant paskutinius pardavimo metus (pvz., Q1 + Q2 + Q3 + Q4) ir padalinant iš keturių.
Šis metodas sušvelnina metinius pokyčius ir leidžia gerai suprasti bendrą metinių pardavimų tendenciją. Slenkamasis vidurkis padeda nurodyti augimo tendenciją, išreikštą procentais. Būtent ši ekstrapoliacija pirmiausia bus naudojama numatant būsimų pardavimų kelią. Tai galima padaryti matematiškai naudojant skaičiuoklę. Arba ekstrapoliuotą tendenciją galima tiesiog nubraižyti diagramoje kaip apytikslę sąmatą.
Tendencijų koreliacija
Visada viena technologija yra kitos pirmtakas. Tai atsitinka, kai pirmtakų technologijos pažangą gali pritaikyti sekėjų technologijos. Kai tokie santykiai egzistuoja, žinios apie pirmtakų technologijos pokyčius gali būti panaudotos numatant technologijos pasekėjų pažangą ateityje. Be to, pirmtako ekstrapoliacija leidžia numatyti sekimą tęsti vėliau.
Šiuo atveju naudojamas tendencijų ekstrapoliacijos metodas, kuriame, pavyzdžiui, lyginamos karinių ir transporto orlaivių greičio tendencijos. Kitas tendencijų koreliacijos prognozavimo pavyzdys yra būsimų kompiuterių dydžio ir galios numatymas remiantis mikroelektronikos technologijos pažanga. Kartais pasekėjų technologija priklauso nuo kelių pirmtakų technologijų, bet ne nuo vieno pirmtako.
Fiksuoti pirmtakų deriniai gali turėti įtakos sekos pokyčiams, tačiau dažniausiai deriniai nėra fiksuojami, o pirmtakų įėjimai skiriasi tiek deriniu, tiek stiprumu. Pavyzdžiui, orlaivio greitis gali padidėti pagerėjus varikliams, medžiagoms, valdikliams, degalams, aerodinamikai ir įvairiems šių veiksnių deriniams.
Koreliacijos prognozės, gautos ekstrapoliuojant tendencijas, pavyzdys: visos keleivių mylios, visos geografinės mylios ir vidutinė tūpimo galia.Statistiškai nustatytų tendencijų ekstrapoliacija leidžia objektyviai prognozuoti. Tačiau šis požiūris turi rimtų apribojimų ir trūkumų. Visos klaidos ar neteisingas pasirinkimas, padarytas nustatant istorinius duomenis, atsispindės prognozėje, o tai sumažina jos vertę.
Programos, atributai ir apribojimai
Ekstrapoliacijos metodas priklauso prognozavimo sričiai. Jis siūlo, kad praeityje egzistavę modeliai išliktų ir ateityje ir kad šie modeliai yra reguliarūs ir gali būti išmatuoti. Kitaip tariant, praeitis yra geras ateities rodiklis. Programos yra naudingos pradiniams duomenims kurti.
Atributai ir ribos yra paprasti ir pigūs skaičiavimo įrankiai, taip pat sudėtingi teoriniai modeliai.
- Proceso duomenys - grafikai ir stebėjimai.
- Svarbiausia yra turėti gerą duomenų bazę ir suprasti jos struktūrą.
- Technika yra tinkamiausia, santykis ir pan.
Laikinos standartinės statistinės procedūros neleidžia tiksliai parinkti tendencijų, kurias prognozuotojas gali patogiai ekstrapoliuoti, atlikdamas prognozę ekstrapoliacijos būdu. Tokiais atvejais prognozuotojas gali „pakoreguoti“ statistinius rezultatus naudodamasis spren- dimu. Jis taip pat gali visiškai nepaisyti statistikos ir ekstrapoliuoti visą tendenciją remdamasis vertinimu.
Tokiu būdu sugeneruotos prognozės yra mažiau tikslios nei statistinės prognozės, tačiau nebūtinai jos bus nepatenkinamos. Vienas iš tokios kokybės tendencijos ekstrapoliacijos pavyzdžių yra orlaivio sudėtingumo numatymas. Bandymai kiekybiškai įvertinti šią tendenciją nebuvo sėkmingi. Bet kilnojamųjų ar reguliuojamų orlaivio dalių procentas buvo ekstrapoliuotas atsižvelgiant į tai, kaip dažnai tokie elementai buvo naudojami anksčiau. Šios prognozės buvo gana tikslios.
Konkrečių techninių pokyčių tokiu būdu negalima numatyti, tačiau pokyčių laipsnis gali. Čia pateikiama naudinga planavimo medžiaga, nurodanti ankstesnio elgesio tendencijas.
