Koreliacijos ir regresijos analizė: pavyzdys, užduotys, taikymas. Koreliacijos ir regresinės analizės metodas

Koreliacijos regresijos analizė - Tai yra vienas iš labiausiai paplitusių metodų tiriant skaitinių verčių ryšį. Pagrindinis jos tikslas yra nustatyti ryšį tarp dviejų parametrų ir jo laipsnio su vėlesne lygties išvestimi. Pavyzdžiui, turime studentų, išlaikiusių matematikos ir anglų kalbos egzaminus. Mes galime naudoti koreliaciją, kad nustatytume, ar vieno testo sėkmė turi įtakos kito dalyko rezultatams. Kalbant apie regresinę analizę, tai padeda numatyti matematikos pažymius pagal anglų kalbos egzamino metu surinktus balus ir atvirkščiai.

Kas yra koreliacijos diagrama?

Bet kokia analizė prasideda nuo informacijos rinkimo. Kuo daugiau, tuo tiksliau gautas rezultatas gaunamas. Aukščiau pateiktame pavyzdyje turime dvi disciplinas, kuriose mokiniai turi išlaikyti egzaminą. Jų sėkmės procentas yra apytikslis. Koreliacijos-regresijos analizė parodo, ar vieno dalyko rezultatas turi įtakos taškų, surinktų antrame egzamine, rezultatams. Norint atsakyti į šį klausimą, būtina lygiagrečiai išanalizuoti visų studentų įvertinimus. Bet pirmiausia turite nuspręsti dėl priklausomo kintamojo. Šiuo atveju tai nėra taip svarbu. Tarkime, matematikos egzaminas vyko anksčiau. Taškai ant jo yra nepriklausomas kintamasis (jie atidedami išilgai abscisės). Anglų kalba įtraukta į tvarkaraštį vėliau. Todėl tuo paremti įverčiai yra priklausomas kintamasis (nubraižomi palei ordinatę). Kuo labiau tokiu būdu gauta diagrama atrodo tiesi, tuo stipresnė yra tiesinė koreliacija tarp dviejų pasirinktų verčių. Tai reiškia, kad matematikos studentai labiau vertina anglų kalbos egzaminą penketukais.

Prielaidos ir supaprastinimai

Koreliacijos ir regresinės analizės metodas apima priežastinio ryšio nustatymą. Tačiau pirmame etape jūs turite suprasti, kad abiejų kiekių pokyčiai gali atsirasti dėl trečiojo, į kuriuos tyrėjas dar neatsižvelgė. Tarp kintamųjų taip pat gali būti nelinijinių ryšių, todėl gauti koeficientą, lygų nuliui, nėra eksperimento pabaiga.

Pirsono tiesinė koreliacija

Šis koeficientas gali būti naudojamas esant dviem sąlygoms. Pirmasis - visos kintamųjų reikšmės yra racionalūs skaičiai, antrasis - tikimasi, kad vertės kinta proporcingai. Šis koeficientas visada yra nuo -1 iki 1. Jei jis yra didesnis nei nulis, tada yra tiesiogiai proporcinga priklausomybė, mažesnė - atvirkščiai, lygi - šios vertės jokiu būdu neturi įtakos viena kitai. Gebėjimas apskaičiuoti šį rodiklį yra koreliacijos ir regresinės analizės pagrindas. Pirmą kartą šį koeficientą sukūrė Karlas Pearsonas, remdamasis Pranciškaus Galtono idėja.

Savybės ir perspėjimai

Pearsono koreliacijos koeficientas yra galingas įrankis, tačiau jį taip pat reikia naudoti atsargiai. Naudojami šie įspėjimai:

1. Pearsono koeficientas rodo tiesinio ryšio buvimą ar nebuvimą. Koreliacijos-regresijos analizė tuo nesibaigia, gali pasirodyti, kad kintamieji vis dėlto yra tarpusavyje susiję.
2. Turi būti atsargūs aiškindami koeficiento vertę. Galima nustatyti koreliaciją tarp kojos dydžio ir IQ lygio.Bet tai nereiškia, kad vienas rodiklis nulemia kitą.
3. Pearsono koeficientas nieko nesako apie priežastinį ryšį tarp rodiklių.

Spearmano rango koreliacijos koeficientas

Jei dėl vieno rodiklio vertės pasikeitimo padidėja arba sumažėja kito rodiklio vertė, tai reiškia, kad jie yra susiję. Koreliacijos-regresijos analizė, kurios pavyzdys bus pateiktas žemiau, yra tiksliai susijusi su tokiais parametrais. Rango koeficientas leidžia supaprastinti skaičiavimus.

Koreliacijos ir regresijos analizė: pavyzdys

Tarkime, kad yra dešimties įmonių efektyvumo įvertinimas. Turime du teisėjus, kurie jiems skiria taškus. Įmonės koreliacijos ir regresijos analizės šiuo atveju negalima atlikti remiantis tiesiniu Pearsono koeficientu. Mums neįdomus teisėjų įvertinimų santykis. Įmonių teisėjai, pasak teisėjų, yra svarbūs.

Šio tipo analizė turi šiuos privalumus:

• Neparametrinė ryšių tarp tirtų dydžių forma.
• Paprastas naudojimas, nes gretas galima priskirti tiek didėjančia reikšmių tvarka, tiek mažėjančia tvarka.

Vienintelis tokio tipo analizės reikalavimas yra būtinybė konvertuoti pirminius duomenis.

Taikymo problemos

Koreliacijos ir regresijos analizė pagrįsta šiomis prielaidomis:

• Stebėjimai laikomi nepriklausomais (penkis kartus padidėjęs „erelis“ neturi įtakos kitos monetos atlenkimo rezultatui).
• Atliekant koreliacijos analizę, abu kintamieji laikomi atsitiktiniais. Regresijoje - tik vienas (priklausomas).
• Testuojant hipotezę, turi būti laikomasi normalaus pasiskirstymo. Priklausomo kintamojo pokytis turėtų būti vienodas kiekvienai abscisės vertei.
• Koreliacijos diagrama yra tik pirmasis hipotezės apie dviejų parametrų serijų ryšį bandymas, o ne galutinis analizės rezultatas.

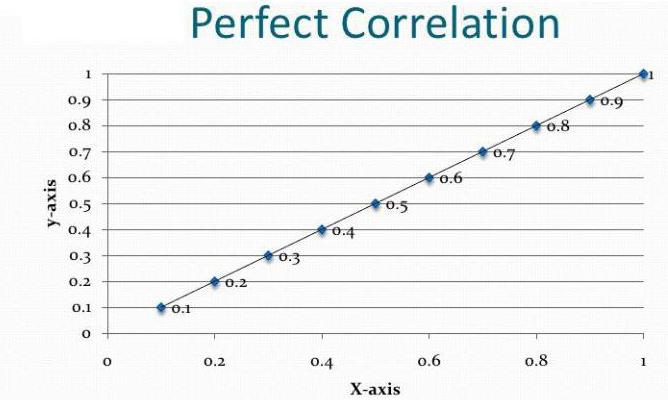
Priklausomybė ir priežastinis ryšys

Tarkime, kad mes apskaičiavome eksporto apimties ir BVP koreliacijos koeficientą. Tai pasirodė lygus vienybės modului. Ar atlikome koreliacijos ir regresijos analizę iki galo? Žinoma, ne. Gautas rezultatas visiškai nereiškia, kad BVP gali būti išreikštas eksportu. Mes dar neįrodėme priežastinio ryšio tarp rodiklių. Koreliacinė-regresinė analizė - vieno kintamojo reikšmių numatymas remiantis kitu. Tačiau jūs turite suprasti, kad dažnai parametrui daro įtaką daugybė veiksnių. Eksportas lemia BVP, bet ne tik jį. Yra ir kiti veiksniai. Čia yra koreliacija ir priežastinis ryšys, nors ir pakoreguotas pagal kitus bendrojo vidaus produkto komponentus.

Kita situacija yra daug pavojingesnė. JK buvo atlikta apklausa, kuri parodė, kad vaikai, kurių tėvai rūkė, dažniau buvo nusikaltėliai. Ši išvada pagrįsta stipria koreliacija tarp rodiklio. Bet ar jis teisingas? Pirma, priklausomybė gali būti atvirkštinė. Tėvai galėjo pradėti rūkyti dėl streso dėl to, kad jų vaikai nuolatos keičiasi ir pažeidžia įstatymus. Antra, abu parametrai gali būti susiję su trečiuoju. Tokios šeimos priklauso žemoms socialinėms klasėms, kurioms būdingos abi problemos. Todėl remiantis koreliacija negalima daryti išvados, kad egzistuoja priežastinis ryšys.

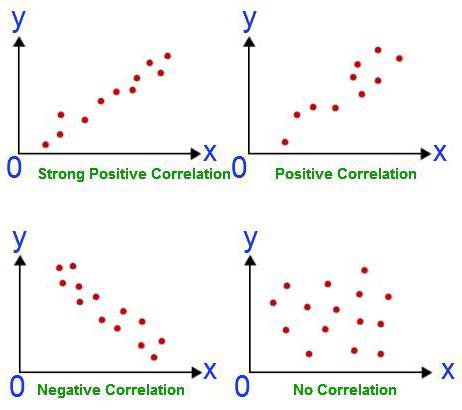
Kodėl verta naudoti regresinę analizę?

Koreliacinė priklausomybė apima ryšių tarp dydžių paiešką. Priežastinis ryšys šiuo atveju išlieka užkulisiuose. Koreliacijos ir regresinės analizės uždaviniai sutampa tik patvirtinant ryšį tarp dviejų dydžių verčių. Tačiau iš pradžių tyrėjas nekreipia dėmesio į priežastinio ryšio galimybę. Regresinė analizė visada turi du kintamuosius, iš kurių vienas yra priklausomas. Tai vyksta keliais etapais:

1. Tinkamo modelio pasirinkimas naudojant mažiausių kvadratų metodą.
2. Lygties, apibūdinančios nepriklausomo kintamojo pokyčio poveikį kitam, išvedimas.

Pvz., Jei tirsime amžiaus įtaką žmogaus augimui, tada regresijos analizė gali padėti numatyti pokyčius bėgant metams.

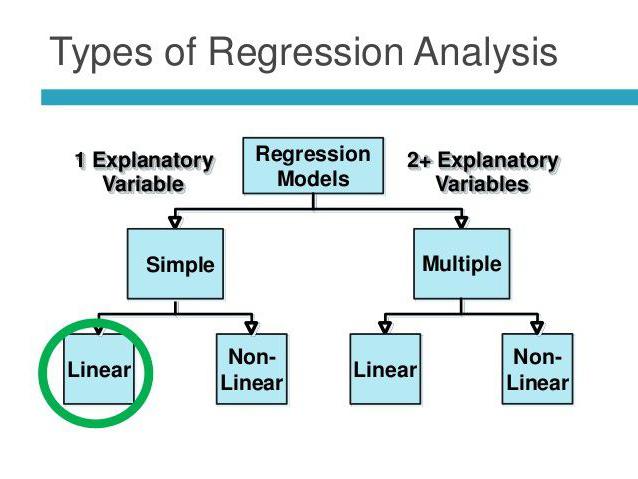
Tiesinė ir daugialypė regresija

Tarkime, kad X ir Y yra du susiję kintamieji. Regresinė analizė leidžia mums numatyti vieno iš jų dydį remiantis kito vertybėmis. Pavyzdžiui, branda ir amžius yra priklausomi simptomai. Santykis tarp jų atspindimas naudojant tiesinę regresiją. Tiesą sakant, jūs galite išreikšti X per Y arba atvirkščiai. Tačiau dažnai teisinga yra tik viena iš regresijos linijų. Analizės sėkmė daugiausia priklauso nuo teisingo nepriklausomo kintamojo nustatymo. Pavyzdžiui, turime du rodiklius: derlių ir kritulius. Iš kasdienės patirties tampa aišku, kad pirmasis priklauso nuo antrojo, o ne atvirkščiai.

Daugybinė regresija leidžia apskaičiuoti nežinomą vertę remiantis trijų ar daugiau kintamųjų vertėmis. Pvz., Ryžių derlingumas vienam žemės akrui priklauso nuo grūdų kokybės, dirvožemio derlingumo, trąšų, temperatūros ir kritulių. Visi šie parametrai turi įtakos bendram rezultatui. Modelio supaprastinimui naudojamos šios prielaidos:

• Ryšys tarp nepriklausomų ir įtaką darančių savybių yra tiesinis.
• Daugialinijiškumas neįtrauktas. Tai reiškia, kad priklausomi kintamieji nėra tarpusavyje susiję.
• Skaičių eilių homoskedasticiškumas ir normalumas.

Koreliacijos ir regresinės analizės taikymas

Yra trys pagrindiniai šio metodo naudojimo atvejai:

1. Atsitiktinių ryšių tarp dydžių tikrinimas. Tokiu atveju tyrėjas nustato kintamojo reikšmes ir išsiaiškina, ar jos turi įtakos priklausomo kintamojo pokyčiui. Pavyzdžiui, galite duoti žmonėms skirtingas alkoholio dozes ir išmatuoti jų kraujospūdį. Šiuo atveju tyrėjas tikrai žino, kad pirmoji yra antrojo priežastis, o ne atvirkščiai. Koreliacijos-regresijos analizė leidžia aptikti tiesiogiai proporcingą tiesinį ryšį tarp šių dviejų kintamųjų ir išvesti formulę, apibūdinančią ją. Tokiu atveju galima palyginti visiškai skirtingomis matavimo vienetais išreikštas vertes.
2. Surasti ryšį tarp dviejų kintamųjų, neišplečiant priežastinio ryšio su jais. Šiuo atveju nėra skirtumo, kokį dydį tyrėjas vadina priklausomu. Be to, iš tikrųjų gali pasirodyti, kad trečiasis kintamasis turi įtakos abiems, todėl jie keičiasi proporcingai.
3. Vieno dydžio verčių apskaičiavimas remiantis kitu. Jis pagrįstas lygtimi, kurioje yra pakeisti žinomi skaičiai.

Taigi koreliacijos analizė apima ryšio (ne priežastinio) tarp kintamųjų suradimą, o regresinė analizė tai paaiškina, dažnai naudodama matematinę funkciją.