Det sammensatte ord "ekstrapolering" er sammensat af to enkle ord. Den første på latin lyder ekstra og betyder "udenfor", "for", "udenfor". Den anden i samme latin lyder polire og betyder "ændring", "rette", "glat". Generelt kan ekstrapolering defineres som en værdi uden for to givne punkter. Det betragtes som en vurdering af, hvad der udvindes fra kendte fakta, der udvider data i et ukendt område for at nå frem til det tilsigtede resultat. Dette koncept kan også tilskrives forudsigelsen af fremtidens image ved at antage sandheden om nutidige og tidligere trends.
Ekstrapolationsmetoden antager, at data eller observationer i fremtiden fortsat vil være ens. Således kan fremtidige resultater forudsiges. Det kan betragtes som en matematisk hypotese. Ekstrapolering bruger dataene og fakta om en bestemt situation og giver forudsigelser om, hvad der kan ske i sidste ende.
Ekstrapolationshistorie

Denne metode omtales ofte som Richardson-ekstrapolering eller Romberg-metoden. Men dette er ikke helt korrekt, da der i århundreder har været lignende numeriske metoder til at løse sådanne problemer. Derfor er den berømte Richardson h2 (ekstrapolering til en numerisk løsning) ikke den første. En lignende metode var anvendelig i Huygens beregninger allerede i 1654. Selve udtrykket "ekstrapolering" blev først opfundet af Thomas D. Clareson i 1959 i en bog om videnskab og fiktion.
Ekstrapoleringsmetoder kan forstås som udvidelsen af data eller processer, hvilket antyder, at en lignende proces vil blive anvendt uden for dem. Ekstrapolering er et vigtigt begreb, der ikke kun bruges i matematik, men også på andre områder, såsom sociologi, psykologi, prognoser. For eksempel ekstrapolerer en chauffør normalt kørselsforhold uden for hans syn. Ekstrapolering kan tilskrives en metode, hvor dataværdier betragtes som punkter x1, x2 ..., xn, og derefter nærmer værdien grænsen for et givet punktinterval.
Fordele ved brug:
- En enkel prognosemetode.
- Der kræves ikke meget data.
- Hurtig og billig analyse.
Metoden findes i statistikker. Hvis nogle værdier periodisk fjernes, nærmer svaret sig det næste datapunkt. Et eksempel på en ekstrapolationsmetode er en vejrudsigt, der undersøger baggrunden for dataene og ekstrapolerer den forudsagte fremtidsmodel. Et endnu enklere eksempel, hvis du har oplysninger om søndage, mandage og tirsdage, kan du ekstrapolere onsdag eller torsdag.
Ulemper ved at bruge ekstrapolering:
- Utillidelighed, hvis der er betydelige udsving i historiske data.
- Antagelsen om, at den seneste tendens vil fortsætte i fremtiden, er næppe mulig i mange konkurrencedygtige forretningsmiljøer.
- Ignorerer kvalitetsfaktorer, såsom ændringer i smag og mode.
Sekvensacceleration
Metoder til ekstrapolering er at skabe en tangentlinie i slutningen af kendte data og udvide dem ud over dette område. Ligesom interpolering bruger ekstrapolering mange metoder, der kræver forudgående viden om processen, der skaber de eksisterende datapunkter. Metoden inkluderer lineær og polynom ekstrapolation, koniske og franske kurveekstrapolering.
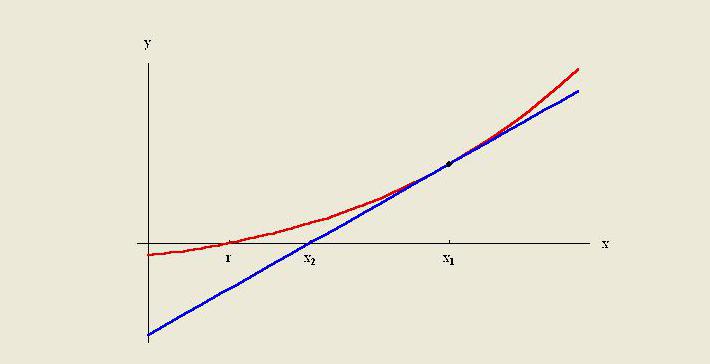
Som regel er kvaliteten af en bestemt metode begrænset af antagelser om funktionen. I numerisk analyse er Richardson-ekstrapolering en sekvensaccelerationsmetode, der bruges til at forbedre konvergenshastigheden.Det er opkaldt efter Lewis Fry Richardson. Han introducerede beregningsteknikken i begyndelsen af det 20. århundrede, hvis brugbarhed til praktiske beregninger næppe kan overvurderes.
Praktiske anvendelser af Richardson-ekstrapolering inkluderer Romberg-integrationen, der anvender den til trapezoidreglen og Bulliers-Stoehr-algoritmen for at løse almindelige differentialligninger.
Lineær metode
Den lineære ekstrapoleringsmetode er nyttig, når der er angivet en lineær funktion. Dette gøres ved at tegne en tangentlinie ved slutpunktet for en given graf og udvide den ud over. Denne metode til ekstrapolering i prognose giver gode resultater, når det punkt, der skal forudsiges, ikke er for langt fra dataene. Lineær interpolation er nyttig til at finde værdier mellem givne punkter. Det kan betragtes som "udfyldning af huller" i datatabellen.
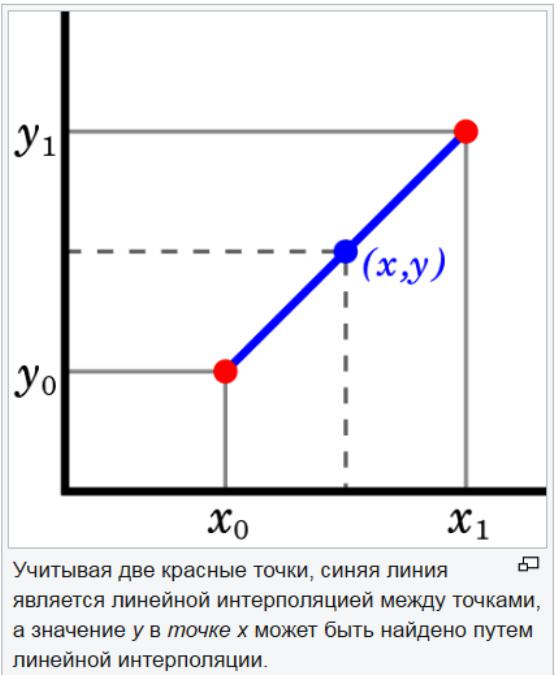
En lineær interpolationsstrategi er at bruge en lige linje til at forbinde kendte værdipunkter på hver side af det ukendte. Lineær interpolation er ikke nøjagtig for ikke-lineære parametre. Hvis punkterne i datasættet ændres med et stort beløb, kan lineær interpolering muligvis give et forkert estimat.
Lineær ekstrapolering kan hjælpe med at estimere værdier, der er højere eller lavere end værdierne i datasættet. Dets strategi er at bruge en undergruppe af data i stedet for hele sættet. For denne type værdi er det nyttigt at anvende ekstrapoleringsmetoden i prognoser ved hjælp af de sidste to eller tre punkter til at estimere en værdi, der overstiger datafeltet.
Polynomiske og koniske ekstrapolationer
Det vides, at tre punkter giver et unikt polynom. En polynomisk kurve kan fortsættes efter afslutningen af sådanne data. Det udføres normalt ved Newton-metoden med en endelig forskel eller ved hjælp af Lagrange-interpolationsformlen. Et polynom af højere orden bør ekstrapoleres med omhu, fordi der er en rimelig chance for fejl med polynom ekstrapolering. Hvis dette sker, vil fejlestimatet stige eksponentielt med graden af polynomet.
I matematik er minimal polynomekstrapolering en sekvenstransformation, der bruges til at fremskynde konvergens. Selvom Aitkens metode er bedst kendt, mislykkes den ofte, især for vektorsekvenser. I dette tilfælde udføres en iteration, der konstruerer matrixen. Dens kolonner er forskelle.

For eksempel kan en ekstrapoleringsmetode til et konisk snit udføres ved hjælp af 5 punkter, der er indikeret nær slutningen af dataene. I tilfælde af at det koniske afsnit er en cirkel eller en ellipse, vil den løbe tilbage og genforenes med sig selv. Parabola eller hyperbola krydser aldrig hinanden. Men de kan bøjes tilbage omkring X-aksen. Ekstrapolering af keglen kan udføres på papir med en konisk sektion eller ved hjælp af en computer.
Matematisk evalueringsmetode
I denne ekstrapolationsmetode er værdien for basisperioden forudsagt. Handlingerne beskrevet nedenfor udføres automatisk af systemet og er ikke synlige for brugeren. Beskrivelsen er beregnet til at forfine algoritmen, der viser de forventede værdier fra den mængde, der er gemt i systemet, og forudsiger resultatet af måleren.
Ekstrapolering ved hjælp af definitionen af mængden af proceduren udføres ved hjælp af funktionen: Yt = f (yi, t, aj).
Som basis for ekstrapolering tilføjes de afrundede data fra en typisk basisperiode, der er gemt i læseresultaterne. Systemet bestemmer vægten Yt af tidsseriedata i t (tidspunkt for prognoseperioden) for at opnå den korrekte løsning ved ekstrapolering. Hvor der på referencepunktet tages yi - niveauet for serien og aj - parameteren for trendligningen.
Feature Prediction
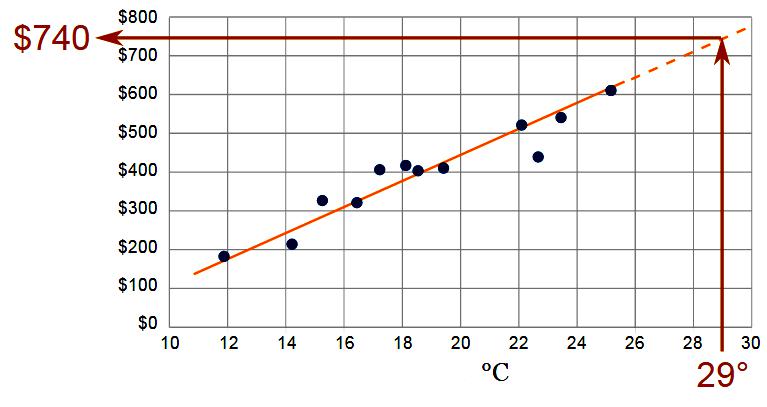
Metoden til fastsættelse af en statistisk kurve kan anvendes til at forudsige funktionalitet.Statistiske procedurer svarer til tidligere data for en eller flere matematiske funktioner, såsom lineær, logaritmisk, Fourier eller eksponentiel. De bedste vælges ved en statistisk test. Derefter ekstrapoleres denne prognose fra denne matematiske forbindelse med metoden til matematisk ekstrapolering. En af de nemmeste måder at få grove skøn over fremtidige (eller tidligere) forhold er at ekstrapolere data, der ændrer sig over tid.
For eksempel, hvis du er nødt til at foretage en grov vurdering af fremtidige niveauer af forurenende stoffer i drikkevand i 20 år i forvejen, kan du ekstrapolere denne tendens fra de sidste 20 år. Det samme ses, hvis du i fremtiden har brug for at estimere forekomsten af rygning eller lungekræft. En prognose kan laves ved at beregne tendenser i de senere år. Ekstrapoleringer af denne type kan udføres ved hjælp af mindre komplekse metoder. I mange tilfælde (især inden for markedsføring og forretningsstyring) bruges ekstrapoleringsmetoden traditionelt, f.eks. Ved at se de nyeste data og intuitivt evaluere, hvad der menes i fremtiden.
Regelbaserede metoder kan også bruges ved at anvende et sæt foruddefinerede principper eller forventninger baseret på en foreløbig forståelse af systemet og under hensyntagen til de nyeste data til fortolkning af fremtidige begivenheder.
Ved enhver ekstrapolationsmetode er forsigtighed vigtig på grund af tilstedeværelsen af adskillige usikkerheder. Enhver ekstrapolationsprocedure er baseret på antagelsen om, at pålidelige oplysninger er tilgængelige i tidligere data og viden. Derfor er fremtiden bestemt af de samme faktorer, som tidligere handlede.
Prognosefejl
Faldet i ekstrapolering (mere præcist, fejlagtigheden af uberettiget ekstrapolering) opstår, når det fænomen, der er ansvarlig for en række trivielle lokale effekter, læses som store globale fænomener. En anden årsag til fejlen er, at nogle gange generaliserede regler trækkes fra for få fakta. Dermed er Darwins evolutionsteori et fantastisk eksempel på anvendelsen af ekstrapolationsmetoden, hvor mekanismerne for tilfældige ændringer og naturlig selektion annonceres for at tage højde for udviklingen af så komplekse strukturer som pattedyrsyn eller immunsystemet for levende organismer.
Ved forsøg på at fortolke forskningsresultater skal forskeren undgå ekstrapolering uden for dataområdet og være opmærksom på de underliggende antagelser for at undgå at acceptere ugyldige konklusioner. Generelt er ekstrapolering et legitimt videnskabeligt værktøj. Der er to aspekter, der hjælper med at skelne mellem gyldig og fejlagtig ekstrapolering. Sandsynligheden for fejlagtig ekstrapolering er højere, når der blev opnået point for utilstrækkelige data for dens konstruktion.
Statistiske værktøjer i Excel
For at finde en sammenhæng mellem år og resultater (for eksempel i en virksomhed) kan du bruge Excel.
Til disse opgaver bruges statistiske værktøjer til ekstrapolationsmodellering, der er indbygget i alle versioner af Excel, startende med 97. Procedure:
- Indtast kendte værdier, for eksempel det samlede salg for 2016-2017, hvis du har brug for at bestemme dem for 2018 og 2020.
- Installer analyse, en funktion, der kræver brug af en tilføjelse.
- For at installere det, trækker du ud fra menuen "Værktøjer", "Tilføjelser".
- Kontroller analysevinduet og bekræft med “OK”.
- Mål korrelationer mellem to serier.
- Den ekstrapolering, der skal udføres, giver kun mening, hvis der er en klar tendens (korrelation) mellem de to sæt sæt (år og salg) ved hjælp af metoden til at ekstrapolere tendenser.
- For at måle denne korrelation skal du bruge menuen "Værktøjer", "Analysehjælpeprogrammer".
- Vælg "Korrelationsanalyse" på listen "Analyseværktøjer" og klik på "OK".
- I feltet Input Range indtastes det analyserede interval, for eksempel A6: B18, Excel tilføjer symbolet "$".
- I området "Output Options" skal du kontrollere outputområdet og indtaste det i det tilstødende felt.
- Bekræft med OK.
- Excel opretter en række to rækker i to kolonner. Find den beregnede værdi (for eksempel 0,981). Da denne værdi er tæt på 1, betyder det, at der er en stærk sammenhæng mellem år og salgstall. Hvis brugeren modtager en værdi tæt på nul, betyder det, at tendensen ikke forekommer. I dette tilfælde giver ekstrapolering ikke mening.
- En evaluering af fremtidige værdier starter.
- Vælg det ønskede interval, og klik på knappen "Chart Wizard".
- Vælg et diagram (for eksempel punktskyer), og klik på Udfør.
Brug af bevægelige gennemsnit
Disse to ekstrapoleringsmetoder involverer den udbredte brug af salgsdata til at forudsige fremtiden. Den glidende gennemsnitsværdi tager en række data og "udjævner" udsving i dem. Målet er at udtrække ekstremaer af data fra periode til periode. Bevægende gennemsnit beregnes ofte kvartalsvis eller ugentligt. For at forudsige fremtidige værdier involverer ekstrapolering brugen af tendenser, der er fastlagt af historiske data. Den største antagelse om ekstrapolering er, at prøven fortsætter i fremtiden, medmindre faktiske beviser tyder på andet. For at forstå disse metoder mere detaljeret kan du overveje et diagram, der viser salget af gadgets til store virksomheder fra 2012 til 2015.
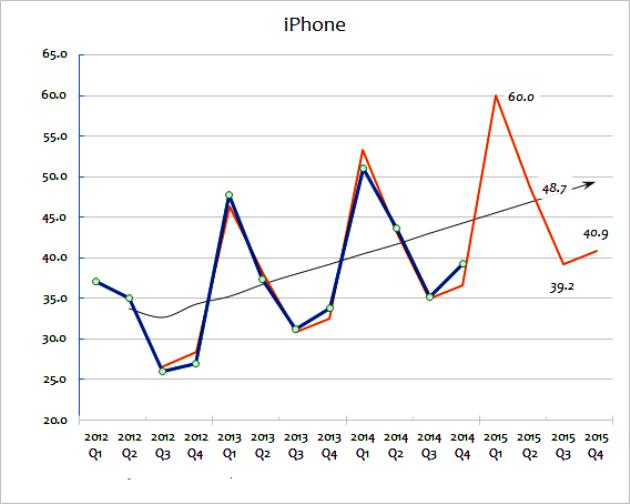
Denne beregningsekstrapoleringsmetode viser det faktiske salgstall. Som du kan se, varierer det samlede salgsmængde fra år til år, selvom du kan gætte (se på dataene), at der er en generel tendens for salgsvækst. Den sorte linje viser det glidende gennemsnit. Dette beregnes ved at tilføje de sidste år med salg (f.eks. Q1 + Q2 + Q3 + Q4) og derefter dividere med fire.
Denne metode udjævner årlige ændringer og giver en god idé om den generelle tendens i årligt salg. Et glidende gennemsnit hjælper med at indikere en væksttrend udtrykt i procent. Det er denne ekstrapolering, der først bruges til at forudsige stien for fremtidig salg. Dette kan gøres matematisk ved hjælp af et regneark. Alternativt kan en ekstrapoleret tendens simpelthen tegnes på et diagram som et groft skøn.
Trend korrelation
En teknologi er altid forløberen for en anden. Dette sker, når de fremskridt, der er gjort inden for forløbet teknologi, kan vedtages ved hjælp af efterfølgende teknologi. Når sådanne forhold eksisterer, kan viden om ændringer i teknologien for forgængere bruges til at forudsige fremskridt for teknologi tilhængere i fremtiden. Derudover muliggør ekstrapolering af forløberen forudsigelse af fortsættelsen af følget ud over tidsforsinkelsen.
I dette tilfælde anvendes trendekstrapoleringsmetoden, hvor for eksempel tendenserne i hastigheden på militære og transportfly sammenlignes. Et andet eksempel på trendkorrelationsprognose er at forudsige størrelsen og effekten af fremtidige computere baseret på fremskridt inden for mikroelektronisk teknologi. Nogle gange afhænger tilhængernes teknologi af flere forløbere teknologier, men ikke af en forgænger.
Faste kombinationer af forgængere kan påvirke ændringen i sekvensen, men oftere er kombinationerne ikke faste, og indgange fra forgængerne er forskellige i både kombination og styrke. For eksempel kan en stigning i flyets hastighed forekomme på grund af forbedring af motorer, materialer, kontroller, brændstof, aerodynamik og forskellige kombinationer af disse faktorer.
Et eksempel på en korrelationsprognose opnået ved ekstrapolering af tendenser: samlet passagermil, samlet geografisk mil og gennemsnitlig landingsstyrke.Ekstrapolering af statistisk bestemte tendenser tillader en objektiv tilgang til prognoser. Imidlertid har denne tilgang alvorlige begrænsninger og faldgruber. Eventuelle fejl eller forkerte valg, der træffes i bestemmelsen af historiske data, afspejles i prognosen, hvilket reducerer deres værdi.
Anvendelser, attributter og grænser
Ekstrapolationsmetoden hører til området for prognoser. Han foreslår, at mønstre, der eksisterede i fortiden, fortsætter ind i fremtiden, og at disse mønstre er regelmæssige og kan måles. Med andre ord er fortiden en god indikator på fremtiden. Programmer er nyttige til at udvikle basisdata.
Attributter og grænser er enkle og billige beregningsværktøjer såvel som komplekse teoretiske modeller.
- Procesdata - grafer og observationer.
- Nøglen er at have en god database og forstå strukturen i den.
- Teknik er den bedste pasform, forholdet og så videre.
Midlertidige standardstatistiske procedurer fører ikke til et nøjagtigt valg af tendenser, som forudsætteren kan ekstrapolere med komfort ved at udføre prognosen ved ekstrapolering. I sådanne tilfælde kan udskærmanden "justere" de statistiske resultater ved hjælp af dom. Det kan også helt ignorere statistikker og ekstrapolere hele tendensen baseret på dømmekraft.
Prognoser, der genereres på denne måde, er mindre nøjagtige end statistiske prognoser, men ikke nødvendigvis utilfredsstillende. Et eksempel på en sådan ekstrapolering af en kvalitetstrend er at forudsige flykompleksitet. Forsøg på at kvantificere denne tendens har ikke været succesrige. Men procentdelen af bevægelige eller justerbare dele af flyet blev ekstrapoleret med den hyppighed, som sådanne elementer blev introduceret i fortiden. Disse prognoser var ret nøjagtige.
Specifikke tekniske ændringer kan ikke forudsiges på denne måde, men graden af ændring kan. Dette giver nyttige planlægningsmaterialer, der indikerer en tendens i tidligere adfærd.
