Korrelations- og regressionsanalyse: eksempel, opgaver, anvendelse. Metode til korrelation og regressionsanalyse

Korrelationsregressionsanalyse - Dette er en af ​​de mest almindelige metoder til at studere forholdet mellem numeriske værdier. Dets hovedmål er at finde forholdet mellem de to parametre og deres grad med den efterfølgende afledning af ligningen. For eksempel har vi studerende, der har bestået matematik- og engelskeksamen. Vi kan bruge korrelation til at bestemme, om succes med en test påvirker resultaterne i et andet emne. Med hensyn til regressionsanalyse hjælper det med at forudsige matematiske karakterer baseret på de point, der blev scoret i en engelsk eksamen, og vice versa.

Hvad er et sammenligningskort?

Enhver analyse begynder med indsamlingen af ​​information. Jo mere det er, jo mere præcist opnås resultatet til sidst. I ovenstående eksempel har vi to discipliner, hvor de studerende skal bestå en eksamen. Deres succesrate er et skøn. Korrelations-regressionsanalyse viser, om resultatet af et individ påvirker de point, der blev scoret i den anden eksamen. For at besvare dette spørgsmål er det nødvendigt at analysere klassificeringen af ​​alle studerende parallelt. Men først skal du beslutte den afhængige variabel. I dette tilfælde er det ikke så vigtigt. Antag, at en matematikeksamen fandt sted tidligere. Punkter på det er en uafhængig variabel (de udsættes langs abscissen). Engelsk er på skemaet senere. Derfor er estimater baseret på den en afhængig variabel (afbildes langs ordinaten). Jo mere den således opnåede graf ligner en lige linje, jo stærkere er den lineære korrelation mellem de to valgte værdier. Dette betyder, at studerende i matematik er mere tilbøjelige til at få femmere i den engelske eksamen.

Antagelser og forenklinger

Metoden til korrelation og regressionsanalyse involverer at finde en årsagssammenhæng. I den første fase skal du dog forstå, at ændringer i begge mængder kan skyldes en tredjedel, som forskeren endnu ikke har taget hensyn til. Der kan også være ikke-lineære forhold mellem variablerne, derfor er det ikke slutningen på eksperimentet at opnå en koefficient lig med nul.

Pearson lineær korrelation

Denne koefficient kan bruges under to betingelser. Den første - alle værdier for variablerne er rationelle tal, den anden - det forventes, at værdierne ændrer sig proportionalt. Denne koefficient er altid mellem -1 og 1. Hvis den er større end nul, er der en direkte proportional afhængighed, mindre - omvendt, lige - disse værdier påvirker ikke hinanden på nogen måde. Evnen til at beregne denne indikator er grundlaget for korrelations- og regressionsanalyse. For første gang blev denne koefficient udviklet af Karl Pearson baseret på ideen om Francis Galton.

Egenskaber og advarsler

Pearsons korrelationskoefficient er et kraftfuldt værktøj, men det bør også bruges med forsigtighed. Følgende advarsler er i brugen:

1. Pearson-koefficienten indikerer tilstedeværelsen eller fraværet af et lineært forhold. Korrelations-regressionsanalyse slutter ikke der, det kan vise sig, at variablerne ikke desto mindre er forbundet med hinanden.
2. Man skal være forsigtig med at fortolke koefficientværdien. Der kan findes en sammenhæng mellem benstørrelse og IQ-niveau.Men dette betyder ikke, at en indikator bestemmer en anden.
3. Pearson-koefficienten siger ikke noget om årsagsforholdet mellem indikatorerne.

Spearmans rangkorrelationskoefficient

Hvis en ændring i værdien af ​​en indikator fører til en stigning eller fald i værdien af ​​en anden, betyder det, at de er relateret. Korrelations-regressionsanalyse, som et eksempel vil blive givet nedenfor, er nøjagtigt forbundet med sådanne parametre. Rank-koefficient giver dig mulighed for at forenkle beregningerne.

Korrelations- og regressionsanalyse: et eksempel

Antag, at der er en vurdering af ti virksomheds resultater. Vi har to dommere, der giver dem point. Korrelations- og regressionsanalyse af virksomheden i dette tilfælde kan ikke udføres på grundlag af den lineære Pearson-koefficient. Vi er ikke interesseret i forholdet mellem dommeres ratings. Virksomhedernes rækker ifølge dommerne er vigtige.

Denne type analyse har følgende fordele:

• Ikke-parametrisk form for forhold mellem de undersøgte mængder.
• Brugervenlighed, fordi rækkerne kan tilskrives både i stigende rækkefølge af værdi og faldende rækkefølge.

Det eneste krav til denne type analyse er behovet for at konvertere kildedataene.

Problemer med applikationen

Korrelations- og regressionsanalysen er baseret på følgende antagelser:

• Observationer betragtes som uafhængige (et femfoldigt tab af "ørnen" påvirker ikke resultatet af den næste møntflip).
• I korrelationsanalysen betragtes begge variabler som tilfældige. I regression - kun én (afhængig).
• Ved test af en hypotese skal en normal distribution overholdes. Ændringen i den afhængige variabel skal være den samme for hver værdi på abscissen.
• Korrelationsdiagrammet er kun den første test af hypotesen om forholdet mellem de to serier af parametre og ikke det endelige resultat af analysen.

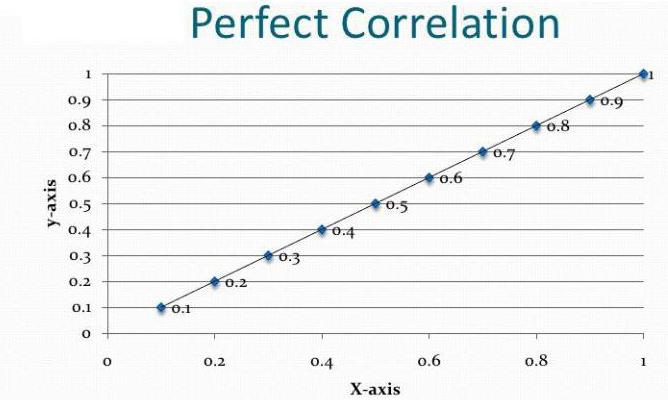
Afhængighed og årsagssammenhæng

Antag, at vi har beregnet korrelationskoefficienten for eksportmængde og BNP. Det viste sig at være lig med enhedsmodulo. Har vi foretaget korrelation og regressionsanalyse til slutningen? Selvfølgelig ikke. Det opnåede resultat betyder slet ikke, at BNP kan udtrykkes gennem eksport. Vi har endnu ikke bevist en årsagssammenhæng mellem indikatorer. Korrelations-regressionsanalyse - prognoser værdierne for en variabel baseret på en anden. Du skal dog forstå, at mange faktorer ofte påvirker parameteren. Eksport bestemmer BNP, men ikke kun det. Der er andre faktorer. Her er der en sammenhæng og årsagsforhold, om end justeret for andre komponenter i bruttonationalproduktet.

En anden situation er meget farligere. I England blev der foretaget en undersøgelse, der viste, at børn, hvis forældre ryger, oftere var lovovertrædere. Denne konklusion er baseret på en stærk sammenhæng mellem indikatoren. Men har han ret? For det første kan afhængigheden være omvendt. Forældre kunne begynde at ryge på grund af stress fra det faktum, at deres børn konstant får ændringer og bryder loven. For det andet kan begge parametre skyldes den tredje. Sådanne familier hører til lave sociale klasser, der er kendetegnet ved begge problemer. Baseret på sammenhængen kan det derfor ikke konkluderes, at der er en årsagssammenhæng.

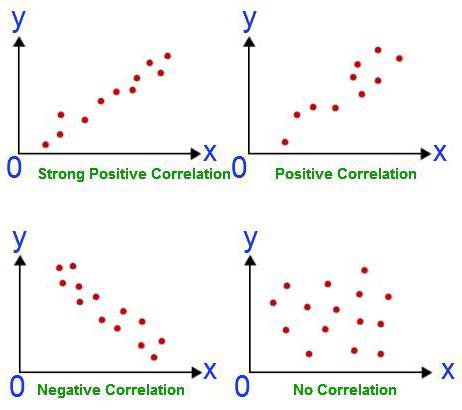
Hvorfor bruge regressionsanalyse?

Korrelation afhænger af at finde sammenhænge mellem mængder. Årsagsforholdet i dette tilfælde forbliver bag kulisserne. Korrelations- og regressionsanalysens opgaver falder kun sammen med hensyn til at bekræfte eksistensen af ​​et forhold mellem værdierne i to mængder. I første omgang er forskeren imidlertid ikke opmærksom på muligheden for en årsagssammenhæng. Regressionsanalyse har altid to variabler, hvoraf den ene er afhængig. Det finder sted i flere faser:

1. Valg af den rigtige model ved hjælp af metoden med mindste firkanter.
2. Afledning af en ligning, der beskriver virkningen af ​​en ændring i en uafhængig variabel på en anden.

Hvis vi for eksempel studerer virkningen af ​​alder på menneskelig vækst, kan en regressionsanalyse hjælpe med at forudsige ændringer gennem årene.

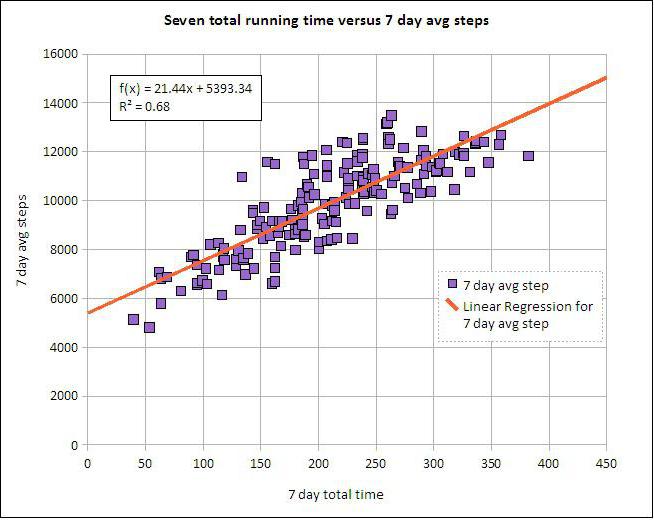
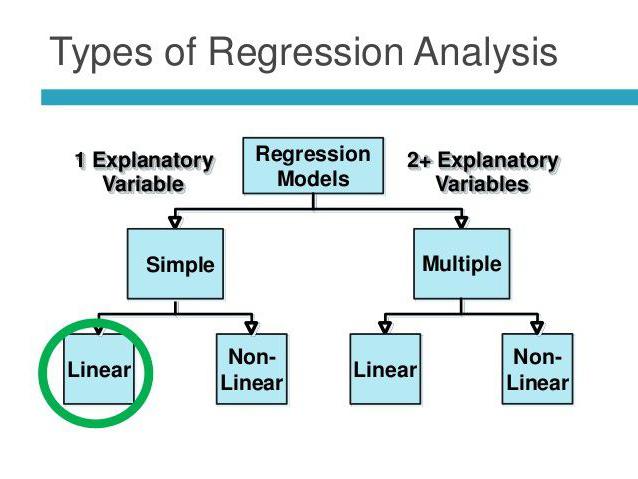
Lineær og multiple regression

Antag, at X og Y er to relaterede variabler. Regressionsanalyse giver os mulighed for at forudsige størrelsen af ​​en af ​​dem baseret på værdierne for den anden. For eksempel er modenhed og alder afhængige symptomer. Forholdet mellem dem afspejles ved hjælp af lineær regression. Faktisk kan du udtrykke X gennem Y eller omvendt. Men ofte er kun en af ​​regressionslinjerne korrekte. Analysens succes afhænger i vid udstrækning af den korrekte bestemmelse af den uafhængige variabel. For eksempel har vi to indikatorer: udbytte og nedbør. Fra hverdagens oplevelse bliver det klart, at den første afhænger af den anden, og ikke omvendt.

Flere regression giver dig mulighed for at beregne en ukendt værdi baseret på værdierne for tre eller flere variabler. For eksempel afhænger risudbyttet pr. Acre jord af kornkvalitet, jordfrugtbarhed, gødning, temperatur og regn. Alle disse parametre påvirker det samlede resultat. For at forenkle modellen bruges følgende antagelser:

• Forholdet mellem uafhængige og påvirkende egenskaber er lineært.
• Multikollinearitet er udelukket. Dette betyder, at afhængige variabler ikke er forbundet.
• Homoskedasticitet og normalitet i række af numre.

Brug af korrelations- og regressionsanalyse

Der er tre hovedtilfælde ved anvendelse af denne metode:

1. Test afslappede forhold mellem mængder. I dette tilfælde bestemmer forskeren værdien af ​​variablen og finder ud af, om de påvirker ændringen i den afhængige variabel. For eksempel kan du give folk forskellige doser alkohol og måle deres blodtryk. I dette tilfælde ved forskeren med sikkerhed, at den første er årsagen til den anden, og ikke omvendt. Korrelations-regressionsanalyse giver dig mulighed for at registrere et direkte proportionalt lineært forhold mellem disse to variabler og udlede en formel, der beskriver den. I dette tilfælde kan værdier udtrykt i helt forskellige måleenheder sammenlignes.
2. At finde et forhold mellem to variabler uden at udvide et årsagsforhold til dem. I dette tilfælde er der ingen forskel, hvilken størrelse forskeren kalder afhængig af. Desuden kan det i virkeligheden vise sig, at begge af dem er påvirket af den tredje variabel, derfor ændrer de sig proportionalt.
3. Beregning af værdier for en mængde baseret på en anden. Det er baseret på en ligning, hvor kendte tal er substitueret.

Således involverer korrelationsanalyse at finde en forbindelse (ikke årsagssammenhæng) mellem variabler, og regressionsanalyse forklarer den, ofte ved hjælp af en matematisk funktion.