คำผสม "การอนุมาน" ประกอบด้วยสองคำง่าย ๆ ตัวแรกในภาษาละตินให้เสียงพิเศษและแปลว่า "นอก", "สำหรับ", "นอก" ครั้งที่สองในภาษาละตินเดียวกันจะมีเสียงโพลและแปลว่า "เปลี่ยน", "ยืด", "เรียบ" โดยทั่วไปการประมาณค่าสามารถถูกกำหนดเป็นค่านอกจุดที่กำหนดสองจุด ถือเป็นการประเมินสิ่งที่ดึงออกมาจากข้อเท็จจริงที่รู้จักซึ่งขยายข้อมูลในพื้นที่ที่ไม่รู้จักเพื่อให้ได้ผลลัพธ์ที่ต้องการ แนวคิดนี้สามารถนำมาประกอบกับการทำนายภาพในอนาคตโดยสมมติความจริงของแนวโน้มปัจจุบันและอดีต
วิธีการอนุมานสันนิษฐานว่าข้อมูลหรือข้อสังเกตในอนาคตจะยังคงเหมือนเดิม ดังนั้นผลลัพธ์ในอนาคตสามารถทำนายได้ มันถือได้ว่าเป็นสมมติฐานทางคณิตศาสตร์ การคาดการณ์ใช้ข้อมูลและข้อเท็จจริงของสถานการณ์เฉพาะและให้การคาดการณ์เกี่ยวกับสิ่งที่อาจเกิดขึ้นในตอนท้าย
การคาดการณ์ประวัติศาสตร์

วิธีนี้มักเรียกกันว่าการคาดการณ์ของริชาร์ดสันหรือวิธี Romberg แต่สิ่งนี้ไม่ถูกต้องอย่างสิ้นเชิงเนื่องจากมีวิธีการเชิงตัวเลขหลายวิธีในการแก้ปัญหาดังกล่าว ดังนั้น Richardson h2 ที่มีชื่อเสียง (การคาดการณ์สำหรับการแก้ปัญหาเชิงตัวเลข) จึงไม่ใช่สิ่งแรก วิธีการที่คล้ายกันมีผลบังคับใช้ในการคำนวณ Huygens เร็วเท่าที่ 1654 คำว่า "การอนุมาน" เป็นคำประกาศเกียรติคุณครั้งแรกของโธมัสดี. แคลร์สันในปี พ.ศ. 2502 ในหนังสือวิทยาศาสตร์และนิยาย
วิธีการคาดการณ์สามารถเข้าใจได้ว่าเป็นส่วนขยายของข้อมูลหรือกระบวนการแนะนำว่ากระบวนการที่คล้ายกันจะถูกนำไปใช้นอกพวกเขา การคาดการณ์เป็นแนวคิดที่สำคัญไม่เพียง แต่ใช้ในวิชาคณิตศาสตร์เท่านั้น แต่ยังรวมถึงในด้านอื่น ๆ เช่นสังคมวิทยาจิตวิทยาการพยากรณ์ ตัวอย่างเช่นคนขับมักจะคาดการณ์สภาพการขับขี่นอกวิสัยทัศน์ของเขา การอนุมานสามารถนำมาประกอบกับวิธีการที่ค่าข้อมูลจะถือว่าเป็นจุด x1, x2 ... , xn และจากนั้นค่าเข้าใกล้ขีด จำกัด ของช่วงของคะแนนที่กำหนด
ประโยชน์ของการใช้งาน:
- วิธีการพยากรณ์อย่างง่าย
- ไม่จำเป็นต้องใช้ข้อมูลมากนัก
- การวิเคราะห์ที่รวดเร็วและราคาถูก
วิธีการมีอยู่ในสถิติ หากมีการลบค่าใด ๆ เป็นระยะคำตอบจะเข้าสู่จุดข้อมูลถัดไป ตัวอย่างของวิธีการคาดการณ์คือการพยากรณ์อากาศซึ่งตรวจสอบภูมิหลังของข้อมูลและคาดการณ์รูปแบบการทำนายอนาคต ตัวอย่างที่ง่ายยิ่งขึ้นหากคุณมีข้อมูลเกี่ยวกับวันอาทิตย์วันจันทร์และวันอังคารคุณสามารถคาดการณ์วันพุธหรือวันพฤหัสบดีได้
ข้อเสียของการใช้การคาดการณ์:
- ไม่น่าเชื่อถือหากมีความผันผวนอย่างมีนัยสำคัญในข้อมูลทางประวัติศาสตร์
- การสันนิษฐานว่าแนวโน้มในอดีตจะดำเนินต่อไปในอนาคตแทบจะเป็นไปไม่ได้ในสภาพแวดล้อมทางธุรกิจที่มีการแข่งขันสูง
- ละเว้นปัจจัยด้านคุณภาพเช่นการเปลี่ยนแปลงรสนิยมและแฟชั่น
การเร่งตามลำดับ
วิธีการคาดการณ์คือการสร้างเส้นสัมผัสในตอนท้ายของข้อมูลที่รู้จักและขยายออกไปนอกพื้นที่นี้ เช่นการแก้ไขการประมาณการณ์ใช้วิธีการต่าง ๆ ที่ต้องการความรู้ก่อนกระบวนการที่สร้างจุดข้อมูลที่มีอยู่ วิธีการดังกล่าวรวมถึงการประมาณเชิงเส้นและพหุนามพหุนามรูปกรวยและการคาดการณ์ส่วนโค้งฝรั่งเศส
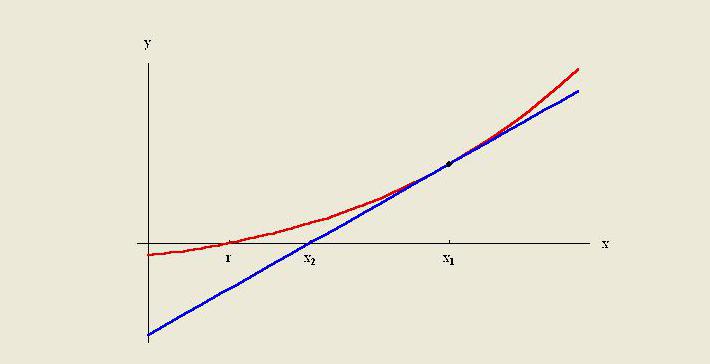
ตามกฎแล้วคุณภาพของวิธีการเฉพาะนั้น จำกัด ด้วยข้อสันนิษฐานเกี่ยวกับฟังก์ชัน ในการวิเคราะห์เชิงตัวเลขการประมาณการณ์ของริชาร์ดสันเป็นวิธีการเร่งความเร็วแบบลำดับที่ใช้เพื่อปรับปรุงอัตราการลู่เข้ามันตั้งชื่อตาม Lewis Fry Richardson เขาแนะนำเทคนิคการคำนวณในตอนต้นของศตวรรษที่ 20 ประโยชน์ของการคำนวณเชิงปฏิบัตินั้นแทบจะไม่สามารถประเมินได้เลย
การใช้งานจริงของการคาดการณ์ของริชาร์ดสันรวมถึงการรวม Romberg ซึ่งใช้กับกฎสี่เหลี่ยมคางหมูและอัลกอริทึม Bulliers-Stoehr เพื่อแก้สมการเชิงอนุพันธ์สามัญ
วิธีการเชิงเส้น
วิธีการอนุมานเชิงเส้นมีประโยชน์เมื่อระบุฟังก์ชันเชิงเส้น สิ่งนี้ทำได้โดยการวาดเส้นสัมผัสที่จุดสิ้นสุดของกราฟที่กำหนดและขยายมันเกิน วิธีการประมาณค่าในการคาดการณ์นี้ให้ผลลัพธ์ที่ดีเมื่อจุดที่คาดการณ์นั้นอยู่ไม่ไกลจากข้อมูล การแก้ไขเชิงเส้นมีประโยชน์ในการค้นหาค่าระหว่างจุดที่กำหนด มันถือได้ว่าเป็น "การเติมช่องว่าง" ของตารางข้อมูล
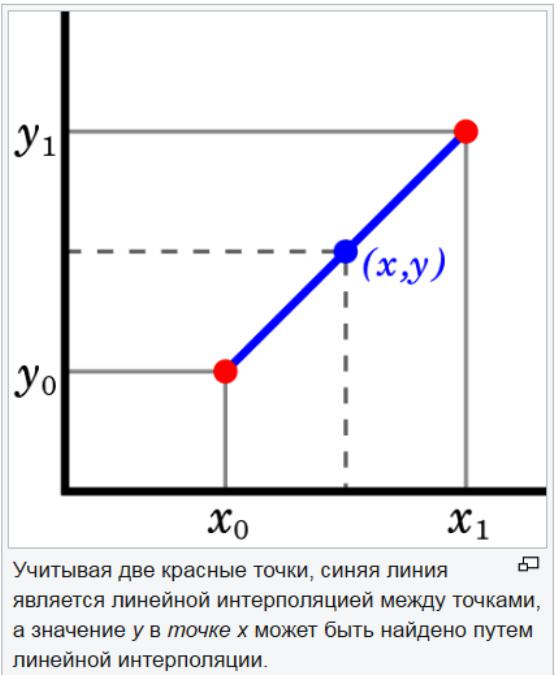
กลยุทธ์การแก้ไขเชิงเส้นคือการใช้เส้นตรงเพื่อเชื่อมต่อจุดที่ทราบค่าของทั้งสองด้านของที่ไม่รู้จัก การประมาณค่าเชิงเส้นไม่แม่นยำสำหรับพารามิเตอร์ที่ไม่ใช่เชิงเส้น หากคะแนนในชุดข้อมูลเปลี่ยนแปลงไปเป็นจำนวนมากการประมาณค่าเชิงเส้นอาจให้ค่าประมาณที่ไม่ถูกต้อง
การประมาณค่าแบบเส้นตรงสามารถช่วยประมาณค่าที่สูงกว่าหรือต่ำกว่าค่าในชุดข้อมูล กลยุทธ์ของมันคือการใช้ชุดย่อยของข้อมูลแทนชุดทั้งหมด สำหรับค่าประเภทนี้จะมีประโยชน์ในการใช้วิธีการคาดการณ์ในการคาดการณ์โดยใช้สองหรือสามจุดสุดท้ายเพื่อประเมินค่าที่เกินช่วงข้อมูล
การประมาณพหุนามและรูปกรวย
มันเป็นที่รู้จักกันว่าสามคะแนนให้พหุนามที่ไม่ซ้ำกัน เส้นโค้งพหุนามสามารถดำเนินการต่อหลังจากสิ้นสุดข้อมูลดังกล่าว มันมักจะดำเนินการโดยวิธีการของนิวตันที่มีความแตกต่างแน่นอนหรือใช้สูตรการแก้ไขลากรองจ์ พหุนามอันดับสูงควรคาดการณ์ด้วยความระมัดระวังเนื่องจากมีโอกาสผิดพลาดในการคาดคะเนกับพหุนามพหุนาม หากสิ่งนี้เกิดขึ้นการประมาณข้อผิดพลาดจะเพิ่มขึ้นแบบเอกซ์โปเนนเชียลโดยมีระดับของพหุนาม
ในวิชาคณิตศาสตร์การประมาณค่าพหุนามน้อยที่สุดเป็นการแปลงแบบลำดับที่ใช้เพื่อเร่งการลู่เข้า แม้ว่าวิธีการของ Aitken จะเป็นที่รู้จักกันดี แต่ก็มักจะล้มเหลวโดยเฉพาะอย่างยิ่งสำหรับลำดับของเวกเตอร์ ในกรณีนี้การทำซ้ำจะดำเนินการที่สร้างเมทริกซ์ คอลัมน์มีความแตกต่าง

ตัวอย่างเช่นวิธีการประมาณค่าสำหรับส่วนรูปกรวยสามารถทำได้โดยใช้ 5 คะแนนที่ระบุใกล้กับจุดสิ้นสุดของข้อมูล ในกรณีที่ส่วนรูปกรวยเป็นวงกลมหรือวงรีก็จะวนกลับและรวมตัวกับตัวเอง Parabola หรือไฮเปอร์โบลาไม่เคยตัดกัน แต่พวกมันสามารถงอกลับได้เกี่ยวกับแกน X การคาดการณ์ของกรวยสามารถทำได้บนกระดาษที่มีส่วนรูปกรวยหรือใช้คอมพิวเตอร์
วิธีการประเมินผลทางคณิตศาสตร์
ในวิธีการประมาณค่านี้จะทำนายค่าสำหรับช่วงเวลาพื้นฐาน การดำเนินการที่อธิบายไว้ด้านล่างนี้ดำเนินการโดยระบบโดยอัตโนมัติและผู้ใช้จะมองไม่เห็น คำอธิบายมีวัตถุประสงค์เพื่อปรับแต่งอัลกอริทึมซึ่งแสดงค่าที่คาดหวังจากจำนวนที่เก็บไว้ในระบบและคาดการณ์ผลลัพธ์ของการวัดมิเตอร์
การคาดการณ์โดยใช้คำจำกัดความของจำนวนขั้นตอนจะดำเนินการโดยใช้ฟังก์ชั่น: Yt = f (yi, t, aj)
เป็นพื้นฐานสำหรับการอนุมานข้อมูลที่ถูกปัดเศษของระยะเวลาพื้นฐานทั่วไปที่เก็บไว้ในผลการอ่านจะถูกเพิ่ม ระบบจะกำหนดน้ำหนัก Yt ของข้อมูลอนุกรมเวลาเป็น t (เวลาของรอบระยะเวลาคาดการณ์) เพื่อขอรับโซลูชันที่ถูกต้องโดยการคาดการณ์ โดยที่จุดอ้างอิงถูกถ่าย yi - ระดับของซีรีย์และ aj - พารามิเตอร์ของสมการแนวโน้ม
การทำนายคุณสมบัติ
วิธีการแก้ไขเส้นโค้งทางสถิติใช้กับการทำนายหน้าที่การใช้งานขั้นตอนทางสถิติสอดคล้องกับข้อมูลในอดีตของฟังก์ชันทางคณิตศาสตร์หนึ่งฟังก์ชันขึ้นไปเช่นเชิงเส้นลอการิทึมฟูริเยร์หรือเลขชี้กำลัง ที่ดีที่สุดจะถูกเลือกโดยการทดสอบทางสถิติ จากนั้นการคาดการณ์นี้ถูกคาดการณ์จากการเชื่อมต่อทางคณิตศาสตร์นี้โดยวิธีการประมาณทางคณิตศาสตร์ หนึ่งในวิธีที่ง่ายที่สุดในการรับประมาณการคร่าวๆเกี่ยวกับเงื่อนไขในอนาคต (หรือในอดีต) คือการคาดการณ์ข้อมูลที่เปลี่ยนแปลงตลอดเวลา
ตัวอย่างเช่นหากคุณจำเป็นต้องประเมินระดับมลพิษในน้ำดื่มในอนาคตเป็นเวลา 20 ปีล่วงหน้าคุณสามารถคาดการณ์แนวโน้มนี้จาก 20 ปีที่ผ่านมา เช่นเดียวกันหากคุณต้องการประเมินความชุกของการสูบบุหรี่หรือมะเร็งปอดในพื้นหลังในอนาคต การคาดการณ์สามารถทำได้โดยการคำนวณแนวโน้มในช่วงหลายปีที่ผ่านมา การคาดการณ์ประเภทนี้สามารถทำได้โดยใช้วิธีการที่ซับซ้อนน้อยกว่า ในหลายกรณี (โดยเฉพาะอย่างยิ่งในด้านการตลาดและการจัดการธุรกิจ) วิธีการอนุมานนั้นใช้แบบดั้งเดิมเช่นโดยการดูข้อมูลล่าสุดและการประเมินอย่างสังหรณ์ใจว่าอะไรจะเกิดขึ้นในอนาคต
วิธีการตามกฎสามารถใช้โดยการใช้ชุดของหลักการที่กำหนดไว้ล่วงหน้าหรือความคาดหวังตามความเข้าใจเบื้องต้นของระบบและคำนึงถึงข้อมูลล่าสุดเพื่อตีความเหตุการณ์ในอนาคต
สำหรับวิธีการประมาณค่าใด ๆ ข้อควรระวังมีความสำคัญเนื่องจากมีความไม่แน่นอนมากมาย ขั้นตอนการอนุมานใด ๆ จะขึ้นอยู่กับสมมติฐานที่ว่าข้อมูลที่เชื่อถือได้มีอยู่ในข้อมูลและความรู้ที่ผ่านมา ดังนั้นอนาคตจะถูกกำหนดโดยปัจจัยเดียวกับที่กระทำก่อนหน้านี้
การพยากรณ์ข้อผิดพลาด
การเข้าใจผิดของการคาดการณ์ (แม่นยำกว่าการเข้าใจผิดของการคาดการณ์ที่ไม่ยุติธรรม) เกิดขึ้นเมื่อปรากฏการณ์ที่รับผิดชอบเกี่ยวกับผลกระทบในท้องถิ่นจำนวนเล็กน้อยนั้นถูกอ่านว่าเป็นปรากฏการณ์ระดับโลกที่ยิ่งใหญ่ อีกเหตุผลหนึ่งที่ทำให้เกิดข้อผิดพลาดก็คือบางครั้งกฎทั่วไปถูกอนุมานจากข้อเท็จจริงที่น้อยเกินไป ดังนั้นทฤษฎีวิวัฒนาการของดาร์วินจึงเป็นตัวอย่างที่ยอดเยี่ยมของการประยุกต์ใช้วิธีการคาดการณ์ซึ่งมีการประกาศกลไกการเปลี่ยนแปลงแบบสุ่มและการคัดเลือกโดยธรรมชาติเพื่อพิจารณาการพัฒนาโครงสร้างที่ซับซ้อนเช่นวิสัยทัศน์ของสัตว์เลี้ยงลูกด้วยนมหรือระบบภูมิคุ้มกันของสิ่งมีชีวิต
เมื่อพยายามตีความผลการวิจัยนักวิทยาศาสตร์ควรหลีกเลี่ยงการคาดการณ์นอกช่วงข้อมูลและตระหนักถึงสมมติฐานที่ตั้งไว้เพื่อหลีกเลี่ยงการยอมรับข้อสรุปที่ไม่ถูกต้อง โดยทั่วไปการคาดการณ์เป็นเครื่องมือทางวิทยาศาสตร์ที่ถูกต้องตามกฎหมาย มีสองด้านที่ช่วยแยกความแตกต่างระหว่างการคาดการณ์ที่ถูกต้องและผิดพลาด ความน่าจะเป็นของการคาดการณ์ที่ผิดพลาดจะสูงขึ้นเมื่อได้รับข้อมูลที่ไม่เพียงพอสำหรับการก่อสร้าง
เครื่องมือทางสถิติของ Excel
ในการค้นหาความสัมพันธ์ระหว่างปีกับผลลัพธ์ (ตัวอย่างเช่นในธุรกิจ) คุณสามารถใช้ Excel
สำหรับงานเหล่านี้มีการใช้เครื่องมือทางสถิติสำหรับการสร้างแบบจำลองการคาดการณ์ที่ใช้กับ Excel ทุกรุ่นเริ่มต้นด้วย 97
- ป้อนค่าที่ทราบเช่นยอดขายรวมสำหรับปี 2559-2560 ถ้าคุณต้องการกำหนดยอดขายสำหรับปี 2561-2563
- ติดตั้งการวิเคราะห์ซึ่งเป็นคุณลักษณะที่ต้องใช้ Add-in
- หากต้องการติดตั้งให้ดึงข้อมูลจากเมนู "เครื่องมือ", "โปรแกรมเสริม"
- ตรวจสอบหน้าต่างยูทิลิตีการวิเคราะห์และยืนยันด้วย“ ตกลง”
- วัดความสัมพันธ์ระหว่างสองชุด
- การคาดการณ์ที่จำเป็นต้องทำนั้นสมเหตุสมผลถ้ามีแนวโน้มชัดเจน (สหสัมพันธ์) ระหว่างตัวเลขสองชุด (ปีกับยอดขาย) โดยวิธีการประมาณแนวโน้ม
- หากต้องการวัดความสัมพันธ์นี้ให้ใช้เมนู "เครื่องมือ", "เครื่องมือวิเคราะห์"
- ในรายการ“ เครื่องมือวิเคราะห์” เลือก“ การวิเคราะห์สหสัมพันธ์” และคลิก“ ตกลง”
- ในฟิลด์ Input Range ป้อนช่วงที่วิเคราะห์ตัวอย่างเช่น A6: B18, Excel จะเพิ่มสัญลักษณ์ "$"
- ในพื้นที่ "ตัวเลือกเอาต์พุต" ให้ตรวจสอบช่วงเอาต์พุตและป้อนในฟิลด์ที่อยู่ติดกัน
- ยืนยันด้วยตกลง
- Excel สร้างอาร์เรย์สองแถวในสองคอลัมน์ ค้นหาค่าที่คำนวณได้ (เช่น 0.981) เนื่องจากค่านี้ใกล้เคียงกับ 1 จึงหมายความว่ามีความสัมพันธ์ที่ดีระหว่างปีกับตัวเลขยอดขาย หากผู้ใช้ได้รับค่าใกล้ศูนย์หมายความว่าแนวโน้มไม่เกิดขึ้น ในกรณีนี้การคาดการณ์ไม่สมเหตุสมผล
- การประเมินค่าในอนาคตเริ่มต้นขึ้น
- เลือกช่วงที่ต้องการแล้วคลิกปุ่ม "ตัวช่วยสร้างแผนภูมิ"
- เลือกแผนภูมิ (ตัวอย่างเช่นชี้กลุ่มเมฆ) และคลิกเสร็จสิ้น
การใช้ค่าเฉลี่ยเคลื่อนที่
วิธีการคาดการณ์ทั้งสองนี้เกี่ยวข้องกับการใช้ข้อมูลการขายอย่างกว้างขวางเพื่อทำนายอนาคต ค่าเฉลี่ยเคลื่อนที่จะใช้ชุดข้อมูลและความผันผวนของ "ราบรื่น" เป้าหมายคือการสกัดข้อมูลส่วนเกินจากช่วงเวลาหนึ่งไปยังอีกช่วงเวลาหนึ่ง ค่าเฉลี่ยเคลื่อนที่มักคำนวณเป็นรายไตรมาสหรือรายสัปดาห์ ในการทำนายค่าในอนาคตการคาดการณ์เกี่ยวข้องกับการใช้แนวโน้มที่กำหนดโดยข้อมูลในอดีต สมมติฐานหลักของการคาดการณ์คือตัวอย่างจะยังคงดำเนินต่อไปในอนาคตเว้นแต่หลักฐานที่แท้จริงจะระบุเป็นอย่างอื่น เพื่อให้เข้าใจถึงวิธีการเหล่านี้อย่างละเอียดยิ่งขึ้นคุณสามารถพิจารณาแผนภูมิที่แสดงยอดขายของแกดเจ็ตสำหรับธุรกิจขนาดใหญ่ตั้งแต่ 2012 ถึง 2015
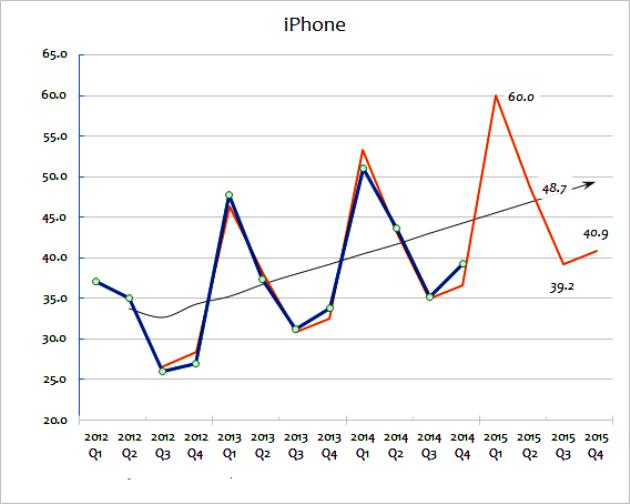
วิธีการอนุมานการคำนวณนี้แสดงตัวเลขยอดขายตามจริง อย่างที่คุณเห็นยอดขายรวมจะแตกต่างกันไปในแต่ละปีถึงแม้ว่าคุณสามารถคาดเดาได้ (ดูข้อมูล) ว่ามีแนวโน้มทั่วไปสำหรับการเติบโตของยอดขาย เส้นสีดำแสดงค่าเฉลี่ยเคลื่อนที่ สิ่งนี้คำนวณโดยการเพิ่มปีสุดท้ายของการขาย (เช่น Q1 + Q2 + Q3 + Q4) จากนั้นหารด้วยสี่
วิธีนี้ทำให้การเปลี่ยนแปลงรายปีราบรื่นและให้ความคิดที่ดีเกี่ยวกับแนวโน้มทั่วไปในการขายประจำปี ค่าเฉลี่ยเคลื่อนที่ช่วยระบุแนวโน้มการเติบโตซึ่งแสดงเป็นเปอร์เซ็นต์ นี่เป็นการคาดการณ์ที่จะใช้ก่อนเพื่อทำนายเส้นทางของยอดขายในอนาคต สามารถทำได้ทางคณิตศาสตร์โดยใช้สเปรดชีต อีกวิธีหนึ่งคือแนวโน้มที่สามารถอนุมานได้ง่าย ๆ บนแผนภูมิเป็นการประมาณคร่าวๆ
แนวโน้มความสัมพันธ์
เทคโนโลยีหนึ่งเสมอคือบรรพบุรุษของเทคโนโลยีอื่น สิ่งนี้จะเกิดขึ้นเมื่อเทคโนโลยีลูกศิษย์สามารถนำไปใช้กับเทคโนโลยีที่ก้าวหน้าได้ เมื่อความสัมพันธ์ดังกล่าวมีอยู่ความรู้เกี่ยวกับการเปลี่ยนแปลงในเทคโนโลยีของรุ่นก่อนสามารถนำมาใช้ในการทำนายความคืบหน้าของผู้ติดตามเทคโนโลยีในอนาคต นอกจากนี้การคาดการณ์ของสารตั้งต้นช่วยให้การทำนายความต่อเนื่องของการติดตามเกินระยะเวลาที่ล่าช้า
ในกรณีนี้มีการใช้วิธีการประมาณค่าของแนวโน้มซึ่งในตัวอย่างนี้มีการเปรียบเทียบแนวโน้มของความเร็วของเครื่องบินทหารและเครื่องบินขนส่ง อีกตัวอย่างหนึ่งของการพยากรณ์ความสัมพันธ์ของแนวโน้มคือการทำนายขนาดและพลังของคอมพิวเตอร์ในอนาคตบนพื้นฐานของความก้าวหน้าทางเทคโนโลยีไมโครอิเล็กทรอนิกส์ บางครั้งเทคโนโลยีของผู้ติดตามขึ้นอยู่กับเทคโนโลยีของผู้นำหลายคน แต่ไม่ใช่ในรุ่นก่อน
การรวมกันของรุ่นก่อนคงที่สามารถส่งผลกระทบต่อการเปลี่ยนแปลงในลำดับ แต่บ่อยครั้งที่ชุดค่าผสมไม่คงที่และอินพุตของรุ่นก่อนจะแตกต่างกันทั้งในชุดค่าผสมและค่าความแข็งแรง ตัวอย่างเช่นการเพิ่มขึ้นของความเร็วเครื่องบินสามารถเกิดขึ้นได้เนื่องจากการปรับปรุงเครื่องยนต์วัสดุการควบคุมเชื้อเพลิงอากาศพลศาสตร์และปัจจัยต่าง ๆ เหล่านี้
ตัวอย่างของการคาดการณ์สหสัมพันธ์ที่ได้รับจากการคาดการณ์แนวโน้ม: ไมล์ผู้โดยสารรวมไมล์ทางภูมิศาสตร์ทั้งหมดและกำลังลงจอดเฉลี่ยการคาดการณ์แนวโน้มที่กำหนดทางสถิติช่วยให้การคาดการณ์มีวัตถุประสงค์ อย่างไรก็ตามวิธีนี้มีข้อ จำกัด และข้อผิดพลาดร้ายแรง ข้อผิดพลาดหรือตัวเลือกที่ไม่ถูกต้องที่เกิดขึ้นในการพิจารณาข้อมูลประวัติจะสะท้อนให้เห็นในการคาดการณ์ซึ่งจะช่วยลดมูลค่า
แอปพลิเคชั่นคุณสมบัติและข้อ จำกัด
วิธีการคาดการณ์เป็นของเขตการพยากรณ์ เขาชี้ให้เห็นว่ารูปแบบที่มีอยู่ในอดีตจะดำเนินต่อไปในอนาคตและรูปแบบเหล่านี้เป็นปกติและสามารถวัดได้ กล่าวอีกนัยหนึ่งอดีตที่ผ่านมาเป็นตัวบ่งชี้ที่ดีสำหรับอนาคต แอปพลิเคชันมีประโยชน์สำหรับการพัฒนาข้อมูลพื้นฐาน
คุณสมบัติและข้อ จำกัด เป็นเครื่องมือคำนวณที่เรียบง่ายและราคาถูกรวมถึงแบบจำลองเชิงทฤษฎีที่ซับซ้อน
- ข้อมูลกระบวนการ - กราฟและการสังเกต
- กุญแจสำคัญคือการมีฐานข้อมูลที่ดีและเข้าใจโครงสร้างภายใน
- เทคนิคเป็นแบบที่ดีที่สุดอัตราส่วนและอื่น ๆ
ขั้นตอนทางสถิติมาตรฐานชั่วคราวไม่ได้นำไปสู่การเลือกแนวโน้มที่แม่นยำซึ่งผู้คาดการณ์สามารถคาดการณ์ได้อย่างสะดวกสบายโดยทำการคาดการณ์ด้วยการคาดการณ์ ในกรณีเช่นนี้ผู้พยากรณ์สามารถ "ปรับ" ผลลัพธ์ทางสถิติโดยใช้วิจารณญาณ นอกจากนี้ยังสามารถเพิกเฉยต่อสถิติอย่างสมบูรณ์และคาดการณ์แนวโน้มทั้งหมดตามการตัดสินใจ
การคาดการณ์ที่สร้างในลักษณะนี้มีความแม่นยำน้อยกว่าการคาดการณ์ทางสถิติ แต่ไม่จำเป็นต้องเป็นที่น่าพอใจ ตัวอย่างหนึ่งของการคาดการณ์แนวโน้มคุณภาพคือการทำนายความซับซ้อนของเครื่องบิน ความพยายามในการหาจำนวนแนวโน้มนี้ยังไม่ประสบความสำเร็จ แต่ร้อยละของชิ้นส่วนที่เคลื่อนย้ายหรือปรับได้ของเครื่องบินถูกคาดการณ์ด้วยความถี่ที่องค์ประกอบดังกล่าวได้รับการแนะนำในอดีต การคาดการณ์เหล่านี้ค่อนข้างแม่นยำ
การเปลี่ยนแปลงทางเทคนิคที่เฉพาะเจาะจงไม่สามารถคาดการณ์ได้ด้วยวิธีนี้ แต่ระดับการเปลี่ยนแปลงสามารถทำได้ สิ่งนี้นำเสนอวัสดุการวางแผนที่มีประโยชน์ซึ่งระบุถึงแนวโน้มในพฤติกรรมที่ผ่านมา
