Korrelasjons- og regresjonsanalyse: eksempel, oppgaver, anvendelse. Metode for korrelasjon og regresjonsanalyse

Korrelasjonsregresjonsanalyse - Dette er en av de vanligste metodene for å studere forholdet mellom tallverdier. Hovedmålet er å finne forholdet mellom de to parameterne og graden av den etterfølgende avledningen av ligningen. For eksempel har vi studenter som har bestått matte- og engelskeksamen. Vi kan bruke korrelasjon for å bestemme om suksessen til en test påvirker resultatene i et annet fag. Når det gjelder regresjonsanalyse, hjelper det å forutsi matematikkarakterer basert på poengene som er oppnådd i en engelsk eksamen, og omvendt.

Hva er et korrelasjonsskjema?

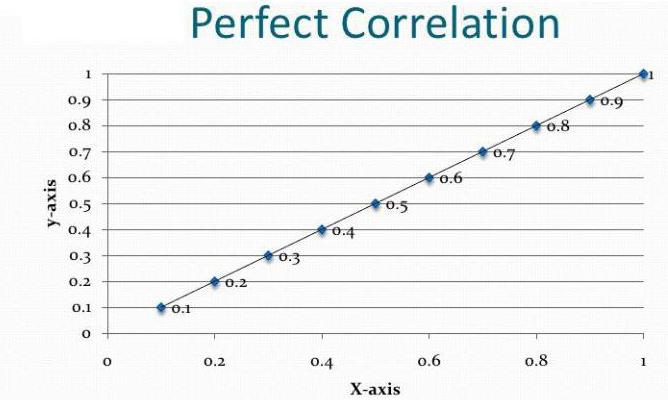
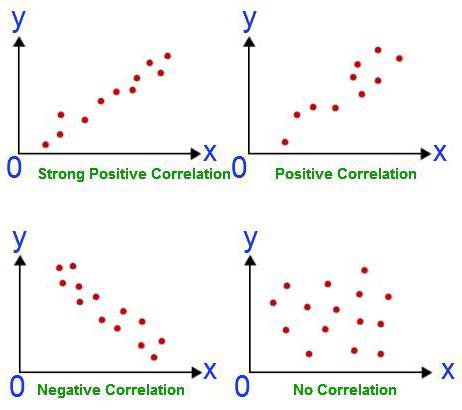
Enhver analyse begynner med innsamling av informasjon. Jo mer det er, desto mer nøyaktig oppnås resultatet til slutt. I eksemplet over har vi to fagfelt der studentene trenger å bestå en eksamen. Deres suksessrate er et anslag. Korrelasjons-regresjonsanalyse viser om resultatet av ett fag påvirker poengene som ble scoret i den andre eksamen. For å svare på dette spørsmålet er det nødvendig å analysere rangeringene til alle studentene parallelt. Men først må du bestemme deg for den avhengige variabelen. I dette tilfellet er det ikke så viktig. Anta at en matteeksamen fant sted tidligere. Poeng på den er en uavhengig variabel (de blir utsatt langs abscissen). Engelsk er på timeplanen senere. Derfor er estimater basert på den en avhengig variabel (plottes langs ordinaten). Jo mer grafen som oppnås slik ser ut som en rett linje, jo sterkere blir den lineære korrelasjonen mellom de to valgte verdiene. Dette betyr at studenter i matematikk har større sannsynlighet for å få femmere i engelskeksamen.

Antagelser og forenklinger

Metoden for korrelasjon og regresjonsanalyse innebærer å finne en årsakssammenheng. Imidlertid må du på det første stadiet forstå at endringer i begge mengder kan skyldes en tredjedel, som forskeren ennå ikke har vurdert. Det kan også være ikke-lineære forhold mellom variablene, og det å oppnå en koeffisient lik null er ikke slutten på eksperimentet.

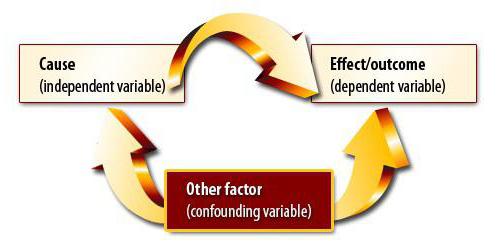
Pearson lineær korrelasjon

Denne koeffisienten kan brukes under to betingelser. Den første - alle verdiene for variablene er rasjonelle tall, den andre - det forventes at verdiene endres proporsjonalt. Denne koeffisienten er alltid mellom -1 og 1. Hvis den er større enn null, er det en direkte proporsjonal avhengighet, mindre - omvendt, lik - disse verdiene påvirker ikke hverandre på noen måte. Evnen til å beregne denne indikatoren er grunnlaget for korrelasjons- og regresjonsanalyse. For første gang ble denne koeffisienten utviklet av Karl Pearson basert på ideen om Francis Galton.

Egenskaper og forsiktighetsregler

Pearsons korrelasjonskoeffisient er et kraftig verktøy, men den bør også brukes med forsiktighet. Følgende advarsler er i bruk:

1. Pearson-koeffisienten indikerer tilstedeværelsen eller fraværet av et lineært forhold. Korrelasjons-regresjonsanalyse slutter ikke der, det kan vise seg at variablene likevel henger sammen.
2. Man må være forsiktig med å tolke koeffisientverdien. En sammenheng kan finnes mellom benstørrelse og IQ-nivå.Men dette betyr ikke at en indikator bestemmer en annen.
3. Pearson-koeffisienten sier ikke noe om årsakssammenhengen mellom indikatorene.

Spearmans rangskorrelasjonskoeffisient

Hvis en endring i verdien til en indikator fører til en økning eller reduksjon i verdien til en annen, betyr dette at de er relatert. Korrelasjons-regresjonsanalyse, hvor et eksempel vil bli gitt nedenfor, er nøyaktig forbundet med slike parametere. Rangeringskoeffisient lar deg forenkle beregningene.

Korrelasjons- og regresjonsanalyse: et eksempel

Anta at det er en vurdering av effektiviteten til ti virksomheter. Vi har to dommere som gir dem poeng. Korrelasjons- og regresjonsanalyse av foretaket i dette tilfellet kan ikke utføres på grunnlag av den lineære Pearson-koeffisienten. Vi er ikke interessert i forholdet mellom dommeres rangeringer. Bedriftenes rekker ifølge dommere er viktige.

Denne typen analyse har følgende fordeler:

• Ikke-parametrisk form for relasjoner mellom de undersøkte mengdene.
• Brukervennlighet, fordi gradene kan tilskrives både i stigende rekkefølge av verdi og synkende rekkefølge.

Det eneste kravet til denne typen analyser er behovet for å konvertere kildedataene.

Problemer med applikasjonen

Korrelasjons- og regresjonsanalysen er basert på følgende forutsetninger:

• Observasjoner blir ansett som uavhengige (et femdoblet tap av "ørnen" påvirker ikke resultatet av neste myntvending).
• I korrelasjonsanalysen blir begge variablene ansett som tilfeldige. I regresjon - bare en (avhengig).
• Når du tester en hypotese, må en normal distribusjon observeres. Endringen i den avhengige variabelen skal være den samme for hver verdi på abscissen.
• Korrelasjonsdiagrammet er bare den første testen av hypotesen om forholdet mellom de to parametrene, og ikke det endelige resultatet av analysen.

Avhengighet og årsakssammenheng

Anta at vi har beregnet korrelasjonskoeffisienten for eksportvolum og BNP. Det viste seg å være lik enhetsmodulo. Har vi gjort korrelasjons- og regresjonsanalyse til slutt? Selvfølgelig ikke. Resultatet oppnår ikke i det hele tatt at BNP kan uttrykkes gjennom eksport. Vi har foreløpig ikke bevist en årsakssammenheng mellom indikatorer. Korrelasjons-regresjonsanalyse - prognoser verdiene til en variabel basert på en annen. Imidlertid må du forstå at ofte mange faktorer påvirker parameteren. Eksport bestemmer BNP, men ikke bare det. Det er andre faktorer. Her er det en sammenheng, og en årsakssammenheng, om enn justert for andre komponenter i bruttonasjonalproduktet.

En annen situasjon er mye farligere. I Storbritannia ble det gjennomført en undersøkelse som viste at barn hvis foreldre røykte, oftere var lovbrytere. Denne konklusjonen er basert på en sterk sammenheng mellom indikatoren. Men har han rett? For det første kan avhengigheten være omvendt. Foreldre kan begynne å røyke på grunn av stress fra det faktum at barna hele tiden får endringer og bryter loven. For det andre kan begge parametrene skyldes den tredje. Slike familier tilhører lave sosiale klasser, som er preget av begge problemer. Basert på korrelasjonen kan det derfor ikke konkluderes med at det er en årsakssammenheng.

Hvorfor bruke regresjonsanalyse?

Korrelasjonsavhengighet innebærer å finne sammenhenger mellom mengder. Årsaksforholdet i dette tilfellet forblir bak kulissene. Oppgavene til korrelasjon og regresjonsanalyse sammenfaller bare når det gjelder å bekrefte eksistensen av et forhold mellom verdiene til to mengder. Til å begynne med legger forskeren imidlertid ikke merke til muligheten for en årsakssammenheng. Regresjonsanalyse har alltid to variabler, hvorav den ene er avhengig. Det foregår i flere trinn:

1. Velge riktig modell ved bruk av metoden med minste kvadrat.
2. Avledning av en ligning som beskriver effekten av en endring i en uavhengig variabel på en annen.

Hvis vi for eksempel studerer effekten av alder på menneskelig vekst, kan en regresjonsanalyse bidra til å forutsi endringer gjennom årene.

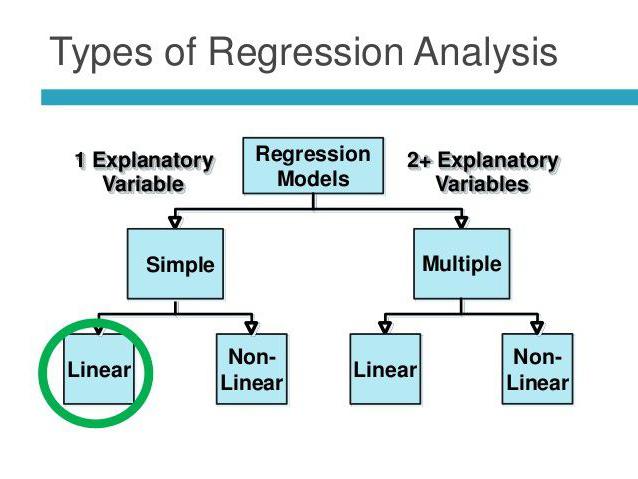
Lineær og multippel regresjon

Anta at X og Y er to relaterte variabler. Regresjonsanalyse lar oss forutsi størrelsen på den ene av dem basert på verdiene til den andre. For eksempel er modenhet og alder avhengige symptomer. Forholdet mellom dem reflekteres ved bruk av lineær regresjon. Faktisk kan du uttrykke X til og med Y eller omvendt. Men ofte er bare en av regresjonslinjene riktig. Suksessen til analysen avhenger i stor grad av riktig bestemmelse av den uavhengige variabelen. For eksempel har vi to indikatorer: utbytte og nedbør. Fra hverdagserfaring blir det tydelig at den første avhenger av den andre, og ikke omvendt.

Flere regresjoner lar deg beregne en ukjent verdi basert på verdiene til tre eller flere variabler. For eksempel er risutbyttet per dekar av land avhengig av kornkvalitet, jordens fruktbarhet, gjødsel, temperatur og nedbør. Alle disse parametrene påvirker det totale resultatet. Følgende forutsetninger brukes for å forenkle modellen:

• Forholdet mellom uavhengige og påvirkende egenskaper er lineært.
• Multikollinearitet er ekskludert. Dette betyr at avhengige variabler ikke henger sammen.
• Homoskedasticitet og normalitet i serien med tall.

Bruken av korrelasjons- og regresjonsanalyse

Det er tre hovedtilfeller ved bruk av denne metoden:

1. Test tilfeldige forhold mellom mengder. I dette tilfellet bestemmer forskeren verdiene til variabelen og finner ut om de påvirker endringen i den avhengige variabelen. For eksempel kan du gi folk forskjellige doser alkohol og måle blodtrykket. I dette tilfellet vet forskeren med sikkerhet at den første er årsaken til den andre, og ikke omvendt. Korrelasjons-regresjonsanalyse lar deg oppdage et direkte proporsjonalt lineært forhold mellom disse to variablene og utlede en formel som beskriver den. I dette tilfellet kan verdier uttrykt i helt forskjellige måleenheter sammenlignes.
2. Å finne et forhold mellom to variabler uten å utvide en årsakssammenheng til dem. I dette tilfellet er det ingen forskjell hvilken størrelse forskeren kaller avhengig av. I virkeligheten kan det dessuten vise seg at begge er påvirket av den tredje variabelen, derfor endres de proporsjonalt.
3. Beregning av verdiene for en mengde basert på en annen. Det er basert på en ligning der kjente tall er erstattet.

Korrelasjonsanalyse innebærer således å finne en sammenheng (ikke årsakssammenheng) mellom variabler, og regresjonsanalyse forklarer den, ofte ved bruk av en matematisk funksjon.