Zložené slovo „extrapolácia“ sa skladá z dvoch jednoduchých slov. Prvý v latinčine znie navyše a znamená „zvonku“, „pre“, „vonku“. Druhý v tej istej latinčine znie polire a znamená „zmena“, „narovnať“, „hladký“. Extrapoláciu možno vo všeobecnosti definovať ako hodnotu mimo dvoch daných bodov. Posudzuje sa, čo sa získava zo známych skutočností, ktoré rozširujú údaje v neznámej oblasti, aby sa dosiahol zamýšľaný výsledok. Túto koncepciu možno pripísať aj predpovedi obrazu budúcnosti, pričom sa vychádza z pravdy o súčasných a minulých trendoch.
Metóda extrapolácie predpokladá, že v budúcnosti budú údaje alebo pozorovania podobné. Takto možno predpovedať budúce výsledky. Možno to považovať za matematickú hypotézu. Extrapolácia využíva údaje a fakty konkrétnej situácie a poskytuje predpovede o tom, čo sa nakoniec môže stať.
História extrapolácie

Táto metóda sa často označuje ako Richardsonova extrapolácia alebo Rombergova metóda. To však nie je úplne správne, pretože už celé storočia existujú podobné numerické metódy na riešenie takýchto problémov. Slávny Richardson h2 (extrapolácia pre číselné riešenie) preto nie je prvý. Podobná metóda bola použiteľná pri výpočtoch Huygensa už v roku 1654. Samotný pojem „extrapolácia“ prvýkrát vytvoril Thomas D. Clareson v roku 1959 v knihe o vede a fikcii.
Metódy extrapolácie sa dajú chápať ako rozšírenie údajov alebo procesov, čo naznačuje, že podobný proces sa bude uplatňovať mimo nich. Extrapolácia je dôležitý pojem používaný nielen v matematike, ale aj v iných oblastiach, ako je sociológia, psychológia, predpovedanie. Napríklad vodič obvykle extrapoluje jazdné podmienky mimo svojho zraku. Extrapoláciu možno pripísať metóde, pri ktorej sa hodnoty údajov považujú za body x1, x2 ..., xn a potom sa hodnota priblíži k limitu daného rozsahu bodov.
Výhody použitia:
- Jednoduchá metóda predpovedania.
- Nie je potrebné veľa údajov.
- Rýchla a lacná analytika.
Metóda existuje v štatistike. Ak sú niektoré hodnoty pravidelne odstraňované, odpoveď sa priblíži k nasledujúcemu údajovému bodu. Príkladom metódy extrapolácie je predpoveď počasia, ktorá berie do úvahy históriu údajov a extrapoluje predpovedaný model budúcnosti. Ešte jednoduchší príklad, ak máte informácie o nedeľu, pondelok a utorok, môžete extrapolovať stredu alebo štvrtok.
Nevýhody použitia extrapolácie:
- Nespoľahlivosť, ak existujú významné výkyvy v historických údajoch.
- Predpoklad, že minulý trend bude pokračovať aj v budúcnosti, je v mnohých konkurenčných podnikateľských prostrediach sotva možný.
- Ignoruje faktory kvality, ako sú zmeny vkusu a módy.
Zrýchlenie sekvencie
Metódou extrapolácie je vytvorenie dotykovej čiary na konci známych údajov a jej rozšírenie za túto oblasť. Podobne ako interpolácia, aj pri extrapolácii sa používa veľa metód, ktoré si vyžadujú predchádzajúcu znalosť procesu, ktorý vytvára existujúce údajové body. Metóda zahŕňa lineárnu a polynómovú extrapoláciu, kužeľovitosť a extrapoláciu francúzskej krivky.
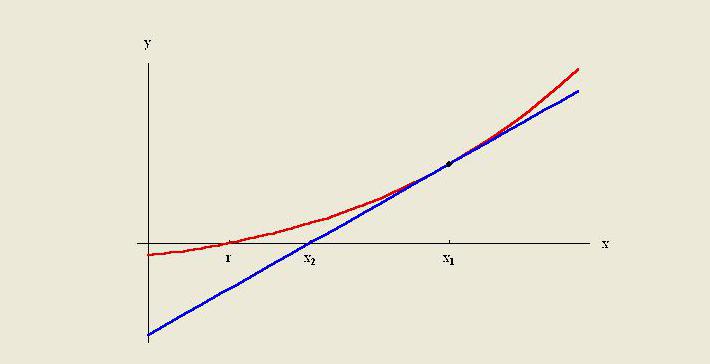
Kvalita konkrétnej metódy je spravidla obmedzená predpokladmi o funkcii. V numerickej analýze je Richardsonova extrapolácia metódou postupného zrýchlenia používaného na zlepšenie rýchlosti konvergencie.Je pomenovaná po Lewisovi Fry Richardsonovi. Na začiatku 20. storočia predstavil výpočtovú techniku, ktorej užitočnosť pre praktické výpočty sa dá len ťažko preceňovať.
Medzi praktické aplikácie Richardsonovej extrapolácie patrí Rombergova integrácia, ktorá ju aplikuje na lichobežníkové pravidlo a Bulliersov-Stoehrov algoritmus na riešenie bežných diferenciálnych rovníc.
Lineárna metóda
Metóda lineárnej extrapolácie je užitočná, keď je špecifikovaná lineárna funkcia. To sa dosiahne nakreslením dotyčnice v koncovom bode daného grafu a jej rozšírením ďalej. Táto metóda extrapolácie pri predpovedaní poskytuje dobré výsledky, keď bod, ktorý sa má predpovedať, nie je príliš vzdialený od údajov. Lineárna interpolácia je užitočná pri zisťovaní hodnôt medzi danými bodmi. Môže sa to považovať za „vyplnenie medzier“ v tabuľke údajov.
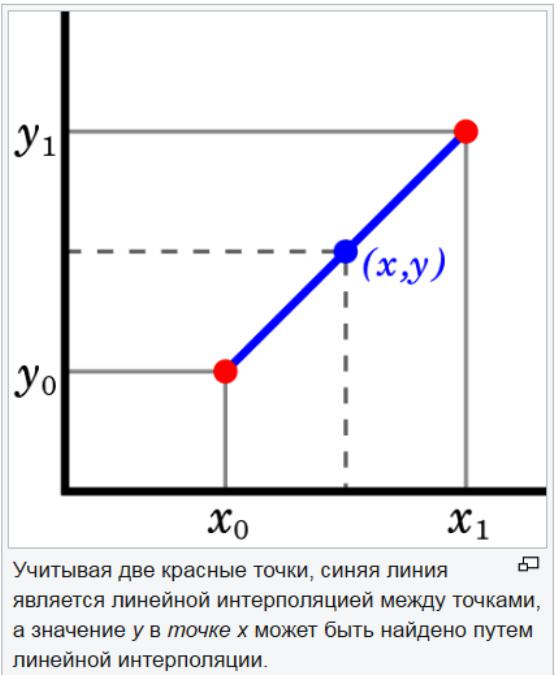
Stratégiou lineárnej interpolácie je použitie priamky na spojenie známych bodov hodnôt na oboch stranách neznáma. Lineárna interpolácia nie je pre nelineárne parametre presná. Ak sa body v súbore údajov zmenia o veľké množstvo, lineárna interpolácia môže poskytnúť nesprávny odhad.
Lineárna extrapolácia môže pomôcť odhadnúť hodnoty, ktoré sú vyššie alebo nižšie ako hodnoty v súbore údajov. Jeho stratégiou je použitie podskupiny údajov namiesto celej sady. Pre tento typ hodnoty je užitočné použiť metódu extrapolácie pri prognózovaní pomocou posledných dvoch alebo troch bodov na odhad hodnoty, ktorá presahuje rozsah údajov.
Polynomické a kónické extrapolácie
Je známe, že tri body poskytujú jedinečný polynóm. Po ukončení takýchto údajov môže polynomická krivka pokračovať. Zvyčajne sa uskutočňuje Newtonovou metódou s konečným rozdielom alebo pomocou Lagrangeovho interpolačného vzorca. Polynóm vyššieho poriadku by sa mal extrapolovať s náležitou starostlivosťou, pretože existuje veľká pravdepodobnosť chyby pri polynómovej extrapolácii. Ak sa tak stane, odhad chyby sa zvýši exponenciálne so stupňom polynómu.
V matematike je minimálna polynomická extrapolácia sekvenčná transformácia používaná na urýchlenie konvergencie. Aj keď je Aitkenova metóda najznámejšia, často zlyháva, najmä pri vektorových sekvenciách. V tomto prípade sa uskutoční iterácia, ktorá vytvára maticu. Jeho stĺpce sú rozdiely.

Napríklad extrapolačnú metódu kužeľovej sekcie je možné vykonať pomocou 5 bodov označených na konci údajov. V prípade, že kužeľovitá časť je kruh alebo elipsa, bude sa slučka pohybovať späť a znova sa spájať so sebou. Parabola alebo hyperbola sa nikdy nepretínajú. Môžu sa však ohnúť späť okolo osi X. Extrapoláciu kužeľa je možné vykonať na papieri s kužeľovou sekciou alebo pomocou počítača.
Metóda matematického hodnotenia
Pri tejto extrapolácii sa predpovedá hodnota pre základné obdobie. Akcie opísané nižšie sú automaticky vykonávané systémom a nie sú pre používateľa viditeľné. Opis je určený na upresnenie algoritmu, ktorý zobrazuje očakávané hodnoty z množstva uloženého v systéme a predpovedá výsledok merania vodomeru.
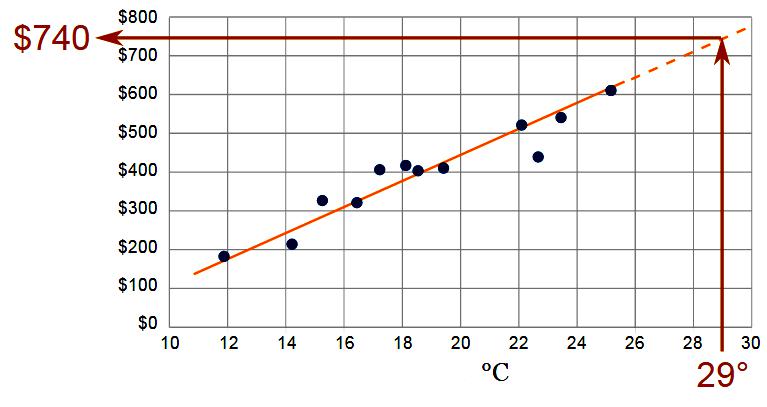
Extrapolácia pomocou definície množstva postupu sa vykonáva pomocou funkcie: Yt = f (yi, t, aj).
Ako základ pre extrapoláciu sa pridajú zaokrúhlené údaje typickej základnej periódy uložené vo výsledkoch čítania. Systém stanoví váhu Yt údajov časových radov vt (čas predpokladaného obdobia), aby sa získalo správne riešenie extrapoláciou. Ak sa berú v referenčnom bode yi - úroveň série a aj - parameter rovnice trendu.
Predpoveď funkcie
Metóda stanovenia štatistickej krivky je použiteľná na predpovedanie funkčnosti.Štatistické postupy zodpovedajú predchádzajúcim údajom jednej alebo viacerých matematických funkcií, ako napríklad lineárnych, logaritmických, Fourierových alebo exponenciálnych. Najlepšie sa vyberajú štatistickým testom. Táto prognóza sa potom extrapoluje z tohto matematického spojenia metódou matematickej extrapolácie. Jedným z najjednoduchších spôsobov, ako získať hrubé odhady budúcich (alebo minulých) podmienok, je extrapolovať údaje, ktoré sa časom menia.
Napríklad, ak potrebujete urobiť hrubé hodnotenie budúcich úrovní znečisťujúcich látok v pitnej vode na 20 rokov vopred, môžete tento trend extrapolovať z posledných 20 rokov. To isté sa pozoruje, ak potrebujete odhadnúť výskyt fajčenia alebo rakoviny pľúc v pozadí v budúcnosti. Prognózu je možné urobiť výpočtom trendov za posledné roky. Extrapolácie tohto typu sa môžu uskutočňovať použitím menej zložitých metód. V mnohých prípadoch (najmä v oblasti marketingu a riadenia podniku) sa metóda extrapolácie tradične používa napríklad prehliadaním najnovších údajov a intuitívnym vyhodnotením toho, čo sa má v budúcnosti myslieť.
Metódy založené na pravidlách môžu byť tiež použité uplatnením súboru preddefinovaných princípov alebo očakávaní založených na predbežnom porozumení systému a pri zohľadnení najnovších údajov pri interpretácii budúcich udalostí.
Pri akejkoľvek metóde extrapolácie je opatrnosť dôležitá z dôvodu výskytu mnohých neistôt. Akýkoľvek postup extrapolácie je založený na predpoklade, že spoľahlivé informácie sú dostupné v minulých údajoch a znalostiach. Budúcnosť je teda určovaná rovnakými faktormi, ktoré konali predtým.
Chyby prognózovania
Klam k extrapolácii (presnejšie klam k neodôvodnenej extrapolácii) sa vyskytuje, keď sa fenomén zodpovedný za množstvo triviálnych lokálnych efektov považuje za veľký globálny fenomén. Ďalším dôvodom chyby je skutočnosť, že niekedy sú všeobecné pravidlá odvodené z príliš malého počtu faktov. Darwinova evolučná teória je teda fantastickým príkladom použitia metódy extrapolácie, pri ktorej sa oznamujú mechanizmy náhodných zmien a prirodzeného výberu, aby sa zohľadnil vývoj takých zložitých štruktúr, ako je videnie cicavcov alebo imunitný systém živých organizmov.
Pri pokusoch o interpretáciu výsledkov výskumu by sa mal vedec vyhnúť extrapolácii mimo rozsahu údajov a mal by si byť vedomý základných predpokladov, aby nedošlo k akceptovaniu neplatných záverov. Extrapolácia je vo všeobecnosti legitímnym vedeckým nástrojom. Existujú dva aspekty, ktoré pomáhajú rozlišovať medzi platnou a chybnou extrapoláciou. Pravdepodobnosť chybnej extrapolácie je vyššia, keď sa pre jej konštrukciu získali body za nedostatočné údaje.
Štatistické nástroje programu Excel
Ak chcete nájsť koreláciu medzi rokmi a výsledkami (napríklad v podnikaní), môžete použiť Excel.
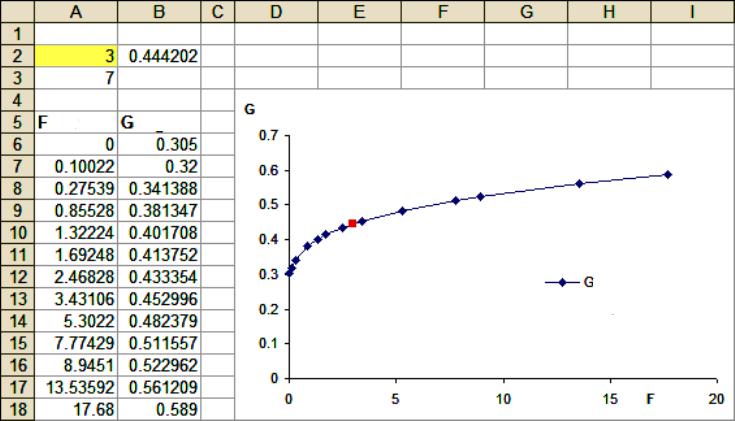
Pre tieto úlohy sa používajú štatistické nástroje na modelovanie extrapolácie, ktoré sú zabudované do všetkých verzií programu Excel, počnúc 97. Postup:
- Zadajte známe hodnoty, napríklad celkový predaj na roky 2016 - 2017, ak ich potrebujete určiť na roky 2018 a 2020.
- Inštalácia analýzy - funkcia, ktorá vyžaduje použitie doplnku.
- Ak ju chcete nainštalovať, vyberte z ponuky „Nástroje“, „Doplnky“.
- Skontrolujte okno pomocného programu pre analýzu a potvrďte tlačidlom „OK“.
- Zmerajte korelácie medzi dvoma sériami.
- Extrapolácia, ktorá sa musí vykonať, má zmysel iba vtedy, ak existuje jasný trend (korelácia) medzi dvoma množinami čísel (roky a tržby) metódou extrapolácie trendov.
- Na meranie tejto korelácie použite ponuku „Nástroje“, „Nástroje na analýzu“.
- V zozname „Analytické nástroje“ vyberte „Korelačná analýza“ a kliknite na „OK“.
- Do poľa Input Range zadajte analyzovaný rozsah, napríklad A6: B18, Excel pridá symbol „$“.
- V oblasti „Možnosti výstupu“ skontrolujte výstupný rozsah a zadajte ho do susedného poľa.
- Potvrďte tlačidlom OK.
- Excel vytvorí pole dvoch riadkov v dvoch stĺpcoch. Nájdite vypočítanú hodnotu (napríklad 0,981). Keďže táto hodnota je blízko 1, znamená to, že existuje silná korelácia medzi rokmi a údajmi o predaji. Ak užívateľ dostane hodnotu blízku nule, bude to znamenať, že trend nenastane. V tomto prípade nemá extrapolácia zmysel.
- Začína sa vyhodnocovanie budúcich hodnôt.
- Vyberte požadovaný rozsah a kliknite na tlačidlo „Sprievodca grafom“.
- Vyberte graf (napríklad bodové oblaky) a kliknite na tlačidlo Dokončiť.
Použitie kĺzavých priemerov
Tieto dve metódy extrapolácie zahŕňajú rozsiahle používanie údajov o predaji na predpovedanie budúcnosti. Hodnota kĺzavého priemeru zaberá sériu údajov a „vyhladzuje“ ich výkyvy. Cieľom je extrahovať extrémy údajov z obdobia na obdobie. Kĺzavé priemery sa často počítajú štvrťročne alebo týždenne. Na predpovedanie budúcich hodnôt zahŕňa extrapolácia použitie trendov stanovených na základe historických údajov. Hlavným predpokladom extrapolácie je, že vzorka bude pokračovať aj v budúcnosti, pokiaľ skutočné dôkazy neuvádzajú inak. Ak chcete podrobnejšie porozumieť týmto metódam, môžete zvážiť graf znázorňujúci predaj miniaplikácií pre veľké podniky od roku 2012 do roku 2015.
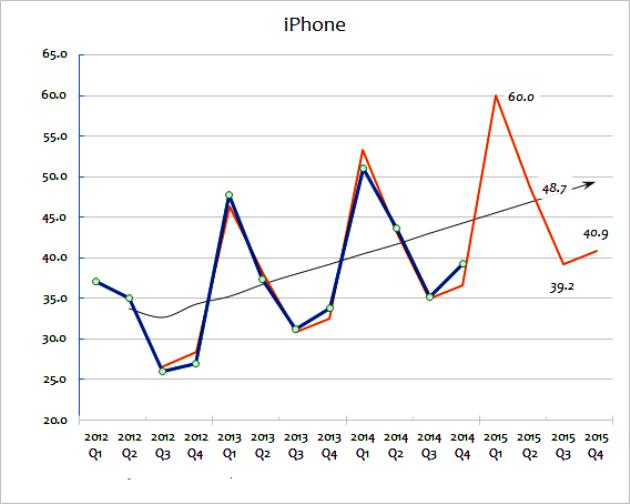
Táto metóda výpočtu extrapolácie ukazuje skutočnú hodnotu predaja. Ako vidíte, celková výška predaja sa z roka na rok líši, aj keď môžete (pri pohľade na údaje) predpokladať, že existuje všeobecný trend rastu predaja. Čierna čiara zobrazuje kĺzavý priemer. Vypočíta sa spočítaním posledných rokov predaja (napr. Q1 + Q2 + Q3 + Q4) a potom vydelením štyrmi.
Táto metóda vyhladzuje ročné zmeny a poskytuje dobrú predstavu o všeobecnom trende ročného predaja. Kĺzavý priemer pomáha naznačovať trend rastu vyjadrený v percentách. Je to táto extrapolácia, ktorá sa použije ako prvá na predpovedanie cesty budúceho predaja. To je možné urobiť matematicky pomocou tabuľky. Alternatívne možno extrapolovaný trend jednoducho vykresliť do grafu ako hrubý odhad.
Korelačná tendencia
Jedna technológia je vždy jej predchodcom. Stáva sa to, keď pokrok dosiahnutý v technológii prekurzorov môže byť prijatý technológiou nasledovníka. Ak takéto vzťahy existujú, znalosť zmien v technológii predchodcov sa môže použiť na predpovedanie pokroku technologických stúpencov v budúcnosti. Extrapolácia prekurzora okrem toho umožňuje predpovedať pokračovanie sledovania po časovom oneskorení.
V tomto prípade sa používa metóda extrapolácie trendov, pri ktorej sa porovnávajú napríklad trendy rýchlosti vojenských a dopravných lietadiel. Ďalším príkladom predikcie korelácie trendov je predpovedanie veľkosti a sily budúcich počítačov na základe pokroku v mikroelektronickej technológii. Technológia nasledovníkov niekedy závisí od viacerých technológií prekurzorov, ale nie od jedného predchodcu.
Pevné kombinácie predchodcov môžu ovplyvniť zmenu v postupnosti, ale častejšie nie sú kombinácie fixné a vstupy predchodcov sa líšia kombináciou aj silou. Napríklad môže dôjsť k zvýšeniu rýchlosti lietadla v dôsledku zlepšenia motorov, materiálov, ovládacích prvkov, paliva, aerodynamiky a rôznych kombinácií týchto faktorov.
Príklad prognózy korelácie získanej extrapoláciou trendov: celkový počet kilometrov cestujúcich, celkový počet geografických kilometrov a priemerný pristávací výkon.Extrapolácia štatisticky určených trendov umožňuje objektívny prístup k predpovedaniu. Tento prístup má však vážne obmedzenia a úskalia. Akékoľvek chyby alebo nesprávne rozhodnutia pri určovaní historických údajov sa odrazia v prognóze, čo znižuje jej hodnotu.
Aplikácie, atribúty a limity
Metóda extrapolácie patrí do oblasti predpovedania. Navrhuje, aby vzorce, ktoré existovali v minulosti, pokračovali aj v budúcnosti a aby boli pravidelne a merateľné. Inými slovami, minulosť je dobrým ukazovateľom budúcnosti. Aplikácie sú užitočné na vývoj základných údajov.
Atribúty a limity sú jednoduché a lacné výpočtové nástroje, ako aj komplexné teoretické modely.
- Procesné dáta - grafy a pozorovania.
- Kľúčom je dobrá databáza a pochopenie štruktúry v nej.
- Technika je najvhodnejšia, pomer a tak ďalej.
Dočasné štandardné štatistické postupy nevedú k presnému výberu trendov, ktoré môže Forecaster pohodlne extrapolovať, pričom prognózu vykonávajú extrapoláciou. V takýchto prípadoch môže Forecaster štatistické výsledky „upraviť“ pomocou úsudku. Môže tiež úplne ignorovať štatistiku a extrapolovať celý trend na základe úsudku.
Prognózy generované týmto spôsobom sú menej presné ako štatistické prognózy, ale nie nevyhnutne neuspokojivé. Jedným z príkladov takejto extrapolácie trendu kvality je predpovedanie zložitosti lietadla. Pokusy kvantifikovať tento trend neboli úspešné. Percento pohyblivých alebo nastaviteľných častí lietadla sa však extrapolovalo frekvenciou, s akou sa tieto prvky v minulosti zavádzali. Tieto predpovede boli pomerne presné.
Týmto spôsobom nie je možné predvídať konkrétne technické zmeny, ale miera zmeny môže byť. Poskytujú užitočné plánovacie materiály, ktoré naznačujú trend v minulosti.
