Det sammensatte ordet "ekstrapolering" er sammensatt av to enkle ord. Den første på latin høres ekstra ut og betyr "utenfor", "for", "utenfor". Den andre i samme latin høres polire ut og betyr "endre", "rette", "glatt". Generelt kan ekstrapolering defineres som en verdi utenfor to gitte punkter. Det anses som en vurdering av hva som er hentet fra kjente fakta som utvider data i et ukjent område for å komme frem til det tiltenkte resultatet. Dette konseptet kan også tilskrives prediksjonen av fremtidens bilde, forutsatt sannheten om nåtidens og fortidens trender.
Ekstrapolasjonsmetoden forutsetter at data eller observasjoner i fremtiden fortsatt vil være like. Dermed kan fremtidige resultater spås. Det kan betraktes som en matematisk hypotese. Ekstrapolering bruker dataene og fakta om en spesifikk situasjon og gir spådommer om hva som kan skje til slutt.
Ekstrapolasjonshistorie

Denne metoden blir ofte referert til som Richardson-ekstrapolering eller Romberg-metoden. Men dette er ikke helt riktig, siden det i århundrer har vært lignende numeriske metoder for å løse slike problemer. Derfor er den berømte Richardson h2 (ekstrapolering for en numerisk løsning) ikke den første. En lignende metode gjaldt i Huygens beregninger allerede i 1654. Selve uttrykket "ekstrapolering" ble først myntet av Thomas D. Clareson i 1959 i en bok om vitenskap og skjønnlitteratur.
Ekstrapoleringsmetoder kan forstås som utvidelsen av data eller prosesser, noe som antyder at en lignende prosess vil bli brukt utenfor dem. Ekstrapolering er et viktig begrep som ikke bare brukes i matematikk, men også på andre områder, som sosiologi, psykologi, prognoser. For eksempel ekstrapolerer en sjåfør kjøreforhold utenfor synet. Ekstrapolering kan tilskrives en metode der dataværdier blir betraktet som punkter x1, x2 ..., xn, og deretter nærmer verdien seg grensen for et gitt poengområde.
Fordeler med bruk:
- En enkel prognosemetode.
- Det kreves ikke mye data.
- Rask og billig analyse.
Metoden finnes i statistikk. Hvis noen verdier blir fjernet med jevne mellomrom, nærmer svaret seg det neste datapunktet. Et eksempel på en ekstrapolasjonsmetode er en værvarsel, som tar hensyn til datahistorikken og ekstrapolerer en forutsagt framtidsmodell. Et enda enklere eksempel, hvis du har informasjon om søndager, mandager og tirsdager, kan du ekstrapolere onsdag eller torsdag.
Ulemper ved bruk av ekstrapolering:
- Upålitelighet, hvis det er betydelige svingninger i historiske data.
- Antagelsen om at den siste trenden vil fortsette i fremtiden er knapt mulig i mange konkurrerende forretningsmiljøer.
- Ignorerer kvalitetsfaktorer, for eksempel forandringer i smak og mote.
Sekvensakselerasjon
Metoder for ekstrapolering er å lage en tangentlinje på slutten av kjente data og utvide den utover dette området. I likhet med interpolering bruker ekstrapolering mange metoder som krever forkunnskaper om prosessen som skaper de eksisterende datapunktene. Metoden inkluderer lineær og polynom ekstrapolasjon, kjegler og fransk kurveekstrapolasjon.
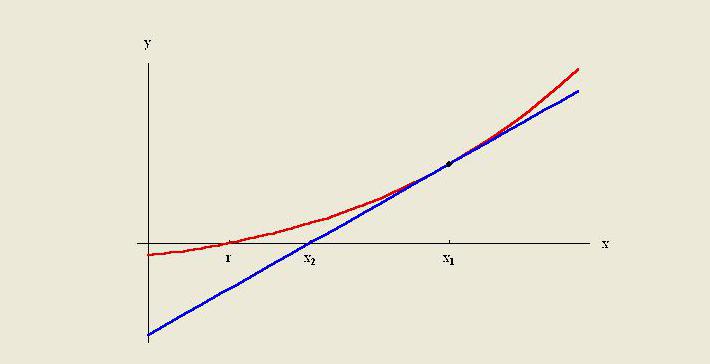
Som regel er kvaliteten på en bestemt metode begrenset av antakelser om funksjonen. I numerisk analyse er Richardson-ekstrapolering en sekvensakselerasjonsmetode som brukes for å forbedre konvergenshastigheten.Den er oppkalt etter Lewis Fry Richardson. Han introduserte beregningsteknikken på begynnelsen av 1900-tallet, og nytten av disse for praktiske beregninger kan vanskelig overvurderes.
Praktiske anvendelser av Richardson-ekstrapolering inkluderer Romberg-integrasjonen, som bruker den på trapesformeregelen og Bulliers-Stoehr-algoritmen for å løse ordinære differensialligninger.
Lineær metode
Den lineære ekstrapolasjonsmetoden er nyttig når en lineær funksjon er spesifisert. Dette gjøres ved å tegne en tangentlinje i sluttpunktet for en gitt graf og utvide den utover. Denne metoden for ekstrapolering i prognoser gir gode resultater når punktet som skal forutsettes ikke er så langt fra dataene. Lineær interpolasjon er nyttig for å finne verdier mellom gitte punkter. Det kan betraktes som "å fylle ut hullene" i datatabellen.
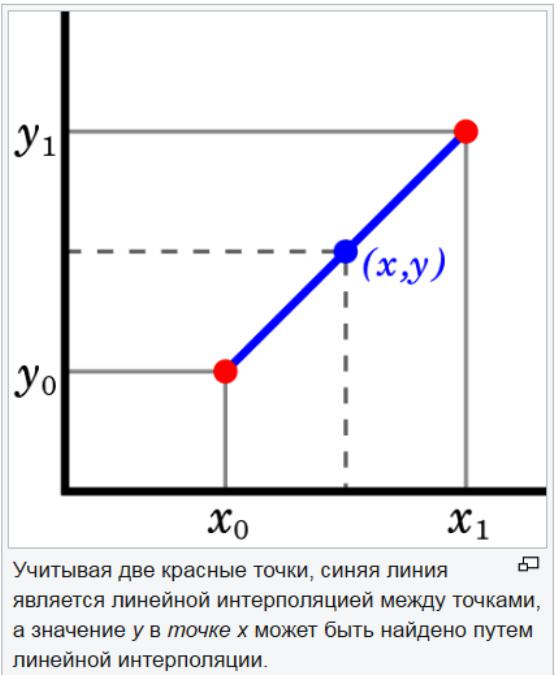
En lineær interpolasjonsstrategi er å bruke en rett linje for å koble sammen kjente verdipunkt på hver side av det ukjente. Lineær interpolasjon er ikke nøyaktig for ikke-lineære parametere. Hvis punktene i datasettet endres med et stort beløp, kan lineær interpolering gi et feil estimat.
Lineær ekstrapolering kan bidra til å estimere verdier som er høyere eller lavere enn verdiene i datasettet. Strategien er å bruke et undersett med data i stedet for hele settet. For denne typen verdi er det nyttig å bruke ekstrapolasjonsmetoden i prognoser ved å bruke de to eller tre siste punktene for å estimere en verdi som overskrider datoperioden.
Polynomiske og koniske ekstrapolasjoner
Det er kjent at tre punkter gir et unikt polynom. En polynomisk kurve kan videreføres etter slutten av slike data. Det utføres vanligvis ved Newton-metoden med en endelig forskjell eller ved bruk av Lagrange-interpolasjonsformelen. Et polynom av høyere orden bør ekstrapoleres med forsiktighet, fordi det er en god sjanse for feil med polynom ekstrapolering. Hvis dette skjer, vil feilestimatet øke eksponentielt med graden av polynomet.
I matematikk er minimal polynom ekstrapolasjon en sekvenstransformasjon som brukes for å akselerere konvergens. Selv om Aitkens metode er mest kjent, mislykkes den ofte, spesielt for vektorsekvenser. I dette tilfellet utføres en iterasjon som konstruerer matrisen. Kolonnene er forskjeller.

For eksempel kan en ekstrapolasjonsmetode for en konisk seksjon lages ved å bruke 5 punkter indikert nær slutten av dataene. I tilfelle den koniske delen er en sirkel eller en ellipse, vil den sløyfe tilbake og gjenforene seg med seg selv. Parabola eller hyperbola krysser aldri hverandre. Men de kan bøyes bak X-aksen. Ekstrapolering av kjeglen kan gjøres på papir med en konisk seksjon eller ved hjelp av en datamaskin.
Matematisk evalueringsmetode
I denne ekstrapolasjonsmetoden er verdien for basisperioden spådd. Handlingene beskrevet nedenfor utføres automatisk av systemet og er ikke synlige for brukeren. Beskrivelsen er ment å avgrense algoritmen, som viser de forventede verdiene fra mengden som er lagret i systemet, og spår resultatet av måleren.
Ekstrapolering ved bruk av definisjonen av mengden av prosedyren utføres ved hjelp av funksjonen: Yt = f (yi, t, aj).
Som et grunnlag for ekstrapolering blir de avrundede dataene fra en typisk basisperiode lagret i leseresultatene lagt til. Systemet bestemmer vekten Yt av tidsseriedata i t (tidspunkt for prognoseperioden) for å oppnå riktig løsning ved ekstrapolering. Hvor på referansepunktet tas yi - nivået på serien og aj - parameteren for trendligningen.
Feature Prediction
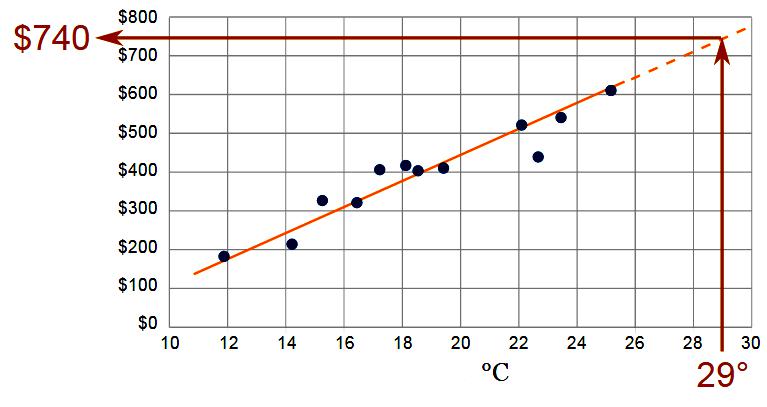
Metoden for å fikse en statistisk kurve kan brukes til å forutsi funksjonalitet.Statistiske prosedyrer samsvarer med tidligere data for en eller flere matematiske funksjoner, for eksempel lineær, logaritmisk, Fourier eller eksponentiell. De beste velges av en statistisk test. Da blir denne prognosen ekstrapolert fra denne matematiske forbindelsen ved hjelp av metoden for matematisk ekstrapolering. En av de enkleste måtene å få grove estimater for fremtidige (eller tidligere) forhold er å ekstrapolere data som endres over tid.
Hvis du for eksempel trenger å gjøre en grov vurdering av fremtidige nivåer av miljøgifter i drikkevann i 20 år på forhånd, kan du ekstrapolere denne trenden fra de siste 20 årene. Det samme observeres hvis du må estimere forekomsten av røyking eller lungekreft i bakgrunnen i fremtiden. En prognose kan gjøres ved å beregne trender de siste årene. Ekstrapoleringer av denne typen kan gjøres ved bruk av mindre komplekse metoder. I mange tilfeller (spesielt innen markedsføring og virksomhetsstyring) brukes ekstrapolasjonsmetoden tradisjonelt, for eksempel ved å se på de nyeste dataene og intuitivt evaluere hva som er ment i fremtiden.
Regelbaserte metoder kan også brukes ved å anvende et sett med forhåndsdefinerte prinsipper eller forventninger basert på en foreløpig forståelse av systemet og ta hensyn til de siste dataene for å tolke fremtidige hendelser.
Med hvilken som helst ekstrapolasjonsmetode er forsiktighet viktig på grunn av tilstedeværelsen av mange usikkerheter. Enhver ekstrapolasjonsprosedyre er basert på antagelsen om at pålitelig informasjon er tilgjengelig i tidligere data og kunnskap. Følgelig bestemmes fremtiden av de samme faktorene som handlet tidligere.
Prognosefeil
Feiligheten i ekstrapolering (mer presist, feilen av uberettiget ekstrapolering) oppstår når fenomenet som er ansvarlig for en rekke trivielle lokale effekter blir lest som store globale fenomener. En annen årsak til feilen er at noen ganger generaliserte regler trekkes fra for få fakta. Dermed er Darwins evolusjonsteori et fantastisk eksempel på anvendelsen av ekstrapolasjonsmetoden, der mekanismene for tilfeldige forandringer og naturlig seleksjon blir kunngjort for å ta hensyn til utviklingen av så komplekse strukturer som pattedyrssyn eller immunsystemet til levende organismer.
Når forskeren prøver å tolke forskningsresultater, bør forskeren unngå ekstrapolering utenfor dataområdet og være klar over de underliggende forutsetningene for å unngå å akseptere ugyldige konklusjoner. Generelt er ekstrapolering et legitimt vitenskapelig verktøy. Det er to aspekter som hjelper til å skille mellom gyldig og feilaktig ekstrapolering. Sannsynligheten for feilaktig ekstrapolering er høyere når poeng for utilstrekkelige data ble oppnådd for konstruksjonen.
Statistiske verktøy for Excel
For å finne en sammenheng mellom år og resultater (for eksempel i en bedrift), kan du bruke Excel.
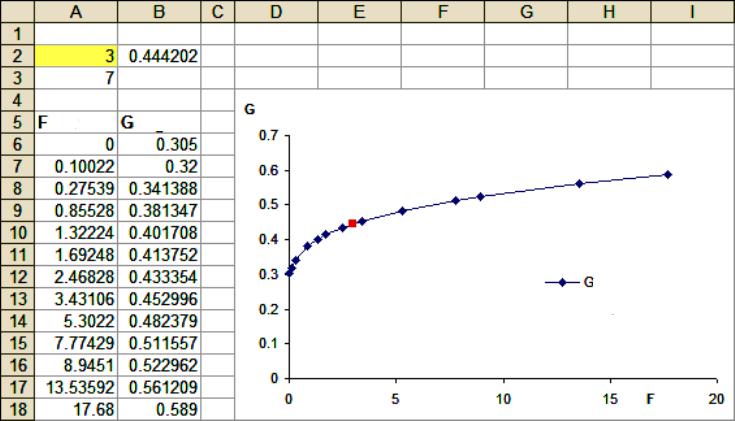
For disse oppgavene brukes statistiske verktøy for ekstrapolasjonsmodellering som er innebygd i alle versjoner av Excel, starter med 97. Prosedyre:
- Angi kjente verdier, for eksempel totalsalg for 2016-2017, hvis du trenger å bestemme dem for 2018 og 2020.
- Installer analyse, en funksjon som krever bruk av et tillegg.
- For å installere det, pakke ut fra menyen "Verktøy", "Tillegg".
- Sjekk analyseverktøyvinduet og bekreft med “OK”.
- Mål korrelasjoner mellom to serier.
- Ekstrapolasjonen som må gjøres gir bare mening hvis det er en klar trend (korrelasjon) mellom de to settene med antall (år og salg) etter metoden for å ekstrapolere trender.
- For å måle denne korrelasjonen, bruk menyen "Verktøy", "Analyseverktøy".
- I listen "Analyseverktøy" velger du "Korrelasjonsanalyse" og klikker "OK".
- Skriv inn det analyserte området i feltet Input Range, for eksempel A6: B18, Excel vil legge til symbolet "$".
- I området "Output Options", sjekk utdataområdet og skriv det inn i det tilstøtende feltet.
- Bekreft med OK.
- Excel oppretter en rekke to rader i to kolonner. Finn den beregnede verdien (for eksempel 0,981). Siden denne verdien er nær 1, betyr det at det er en sterk sammenheng mellom år og salgstall. Hvis brukeren mottar en verdi nær null, vil dette bety at trenden ikke forekommer. I dette tilfellet gir ikke ekstrapolering mening.
- En evaluering av fremtidige verdier starter.
- Velg ønsket område og klikk på "Chart Wizard" -knappen.
- Velg et diagram (for eksempel pekeskyer) og klikk Fullfør.
Bruken av bevegelige gjennomsnitt
Disse to ekstrapolasjonsmetodene innebærer en utbredt bruk av salgsdata for å forutsi fremtiden. Den bevegelige gjennomsnittsverdien tar en serie data og "jevner ut" svingninger i dem. Målet er å trekke ut ekstrem av data fra periode til periode. Rørende gjennomsnitt beregnes ofte kvartalsvis eller ukentlig. For å forutsi fremtidige verdier innebærer ekstrapolering bruk av trender som er etablert av historiske data. Hovedforutsetningen for ekstrapolering er at utvalget vil fortsette i fremtiden, med mindre faktisk bevis tyder på noe annet. For å forstå disse metodene mer detaljert, kan du vurdere et diagram som viser salget av dingser for store bedrifter fra 2012 til 2015.
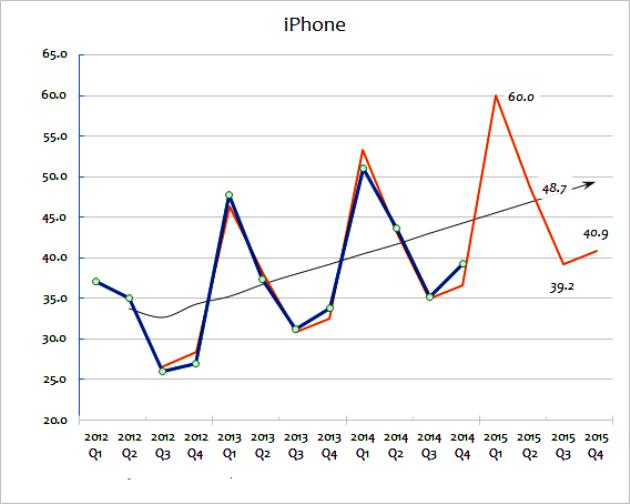
Denne beregningsekstrapolasjonsmetoden viser det faktiske salgstall. Som du ser, varierer den totale mengden salg fra år til år, selv om du kan gjette (se på dataene) at det er en generell trend for salgsvekst. Den svarte streken viser det glidende gjennomsnittet. Dette beregnes ved å legge til de siste årene med salg (f.eks. Q1 + Q2 + Q3 + Q4) og deretter dele med fire.
Denne metoden jevner ut årlige endringer og gir en god ide om den generelle trenden i årssalg. Et glidende gjennomsnitt er med på å indikere en veksttrend, uttrykt i prosent. Det er denne ekstrapolasjonen som først skal brukes til å forutsi banen for fremtidig salg. Dette kan gjøres matematisk ved hjelp av et regneark. Alternativt kan en ekstrapolert trend ganske enkelt tegnes på et diagram som et grovt estimat.
Trendkorrelasjon
Alltid en teknologi er forløperen til en annen. Dette skjer når fremskrittene som gjøres i forløpsteknologi kan bli adoptert av følgeteknologi. Når slike forhold eksisterer, kan kunnskap om forandringer i teknologi til forgjengerne brukes til å forutsi fremgangen til teknologifølgere i fremtiden. I tillegg tillater ekstrapolering av forløperen å forutsi fortsettelsen av følget utover tidsforsinkelsen.
I dette tilfellet brukes metoden for ekstrapolering av trender, der for eksempel trendene i hastigheten til militære og transportfly blir sammenlignet. Et annet eksempel på trendkorrelasjonsvarsling er å forutsi størrelsen og kraften til fremtidige datamaskiner basert på fremskritt innen mikroelektronisk teknologi. Noen ganger er teknologien til følgere avhengig av flere teknologier fra forgjengerne, men ikke av en forgjenger.
Faste kombinasjoner av forgjengerne kan påvirke endringen i sekvensen, men oftere er ikke kombinasjonene faste, og innspillene til forgjengerne skiller seg både i kombinasjon og styrke. For eksempel kan en økning i flyets hastighet oppstå på grunn av forbedring av motorer, materialer, kontroller, drivstoff, aerodynamikk og forskjellige kombinasjoner av disse faktorene.
Et eksempel på en korrelasjonsprognose oppnådd ved ekstrapolering av trender: total passasjermil, total geografisk mil og gjennomsnittlig landingsstyrke.Ekstrapolering av statistisk bestemte trender tillater en objektiv tilnærming til prognoser. Imidlertid har denne tilnærmingen alvorlige begrensninger og fallgruver. Eventuelle feil eller uriktige valg som er gjort i bestemmelsen av historiske data, vil gjenspeiles i prognosen, noe som reduserer deres verdi.
Bruksområder, attributter og grenser
Ekstrapolasjonsmetoden hører til feltet for prognoser. Han antyder at mønstre som eksisterte i fortiden vil fortsette inn i fremtiden, og at disse mønstrene er regelmessige og kan måles. Med andre ord er fortiden en god indikator på fremtiden. Applikasjoner er nyttige for å utvikle basisdata.
Attributter og grenser er enkle og billige beregningsverktøy, så vel som komplekse teoretiske modeller.
- Prosessdata - grafer og observasjoner.
- Nøkkelen er å ha en god database og forstå strukturen i den.
- Teknikk er best passform, forhold og så videre.
Midlertidige statistiske standardprosedyrer fører ikke til nøyaktig utvalg av trender som prognoser kan ekstrapolere med komfort, og utføre prognosen ved ekstrapolering. I slike tilfeller kan prognosemakeren "justere" de statistiske resultatene ved bruk av skjønn. Det kan også ignorere statistikk fullstendig og ekstrapolere hele trenden basert på dømmekraft.
Prognoser generert på denne måten er mindre nøyaktige enn statistiske prognoser, men ikke nødvendigvis utilfredsstillende. Et eksempel på en slik ekstrapolering av en kvalitetstrend er å forutsi flykompleksitet. Forsøk på å tallfeste denne trenden har ikke vært vellykket. Men prosentandelen av bevegelige eller justerbare deler av flyet ble ekstrapolert med frekvensen som slike elementer ble introdusert i fortiden. Disse prognosene var ganske nøyaktige.
Spesifikke tekniske endringer kan ikke forutsies på denne måten, men graden av endring kan. Dette gir nyttige planleggingsmateriell, som indikerer en trend i tidligere oppførsel.
