Složena riječ "ekstrapolacija" sastoji se od dvije jednostavne riječi. Prvo na latinskom jeziku zvuči dodatno i znači "vani", "za", "vani". Drugi na istoj latino zvuči polire i znači "promijeniti", "ispraviti", "glatko". Općenito, ekstrapolacija se može definirati kao vrijednost izvan dvije dane točke. Smatra se procjenom onoga što je izvađeno iz poznatih činjenica koje proširuju podatke u nepoznato područje kako bi se postigao željeni rezultat. Ovaj se koncept može pripisati i predviđanju slike budućnosti, pretpostavljajući istinitost sadašnjih i prošlih trendova.
Metoda ekstrapolacije pretpostavlja da će podaci ili promatranja u budućnosti i dalje biti slični. Tako se mogu predvidjeti budući rezultati. Može se smatrati matematičkom hipotezom. Ekstrapolacija koristi podatke i činjenice o konkretnoj situaciji i daje predviđanja o tome što bi se na kraju moglo dogoditi.
Povijest ekstrapolacije

Ovu se metodu često naziva Richardson-ovom ekstrapolacijom ili Rombergovom metodom. Ali to nije sasvim ispravno, jer stoljećima postoje slične numeričke metode za rješavanje takvih problema. Stoga, poznati Richardson h2 (ekstrapolacija za numeričko rješenje) nije prvi. Slična metoda bila je primjenjiva u Huygensovim proračunima već 1654. Sam izraz "ekstrapolacija" prvi je put skovao Thomas D. Clareson 1959. godine u knjizi o znanosti i fantastici.
Metode ekstrapolacije mogu se shvatiti kao proširenje podataka ili procesa koji sugeriraju da će se sličan postupak primijeniti i izvan njih. Ekstrapolacija je važan pojam koji se koristi ne samo u matematici, već iu drugim područjima, poput sociologije, psihologije, predviđanja. Na primjer, vozač obično ekstrapolira uvjete vožnje izvan svog vida. Ekstrapolacija se može pripisati metodi u kojoj se vrijednosti podataka tretiraju kao točke x1, x2 ..., xn, a zatim se vrijednost približava granici određenog raspona točaka.
Prednosti upotrebe:
- Jednostavna metoda predviđanja.
- Nije potrebno mnogo podataka.
- Brza i jeftina analitika.
Metoda postoji u statistici. Ako se bilo koje vrijednosti povremeno uklanjaju, odgovor se približava sljedećoj točki podataka. Primjer ekstrapolacijske metode je vremenska prognoza koja ispituje pozadinu podataka i ekstrapolira predviđeni model budućnosti. Još jednostavniji primjer, ako imate informacije o nedjeljom, ponedjeljkom i utorkom, možete ekstrapolirati srijedu ili četvrtak.
Nedostaci upotrebe ekstrapolacije:
- Nepouzdanost, ako postoje značajna kolebanja povijesnih podataka.
- Pretpostavka da će se prošli trend nastaviti u budućnosti teško je moguća u mnogim konkurentnim poslovnim okruženjima.
- Zanemaruje čimbenike kvalitete, poput promjena ukusa i mode.
Ubrzanje slijeda
Metode ekstrapolacije je stvoriti tangencijalnu liniju na kraju poznatih podataka i proširiti je izvan ovog područja. Kao i interpolacija, ekstrapolacija koristi mnoge metode za koje je potrebno prethodno znanje o procesu koji stvara postojeće podatkovne točke. Metoda uključuje linearnu i polinomnu ekstrapolaciju, konike i ekstrapolaciju francuske krivulje.
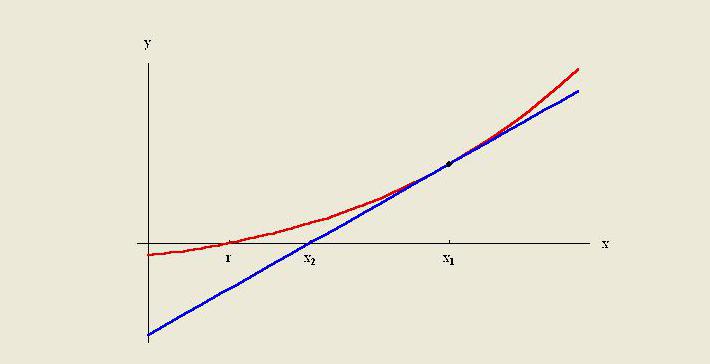
U pravilu je kvaliteta određene metode ograničena pretpostavkama o funkciji. U numeričkoj analizi, Richardson ekstrapolacija je metoda ubrzanja sekvence koja se koristi za poboljšanje brzine konvergencije.Ime je dobio po Lewisu Fry Richardsonu. On je uveo tehniku izračuna početkom 20. stoljeća, čija se korisnost za praktične proračune teško može precijeniti.
Praktične primjene Richardsonove ekstrapolacije uključuju Rombergovu integraciju, koja se primjenjuje na trapezoidno pravilo i algoritam Bulliers-Stoehr za rješavanje običnih diferencijalnih jednadžbi.
Linearna metoda
Metoda linearne ekstrapolacije korisna je kada je navedena linearna funkcija. To se postiže izvlačenjem tangencijalne crte na krajnjoj točki određenog grafa i širenjem izvan njega. Ova metoda ekstrapolacije u prognoziranju daje dobre rezultate kada točka koju treba predvidjeti nije predaleko od podataka. Linearna interpolacija korisna je u pronalaženju vrijednosti između danih točaka. Može se smatrati "popunjavanjem praznina" tablice podataka.
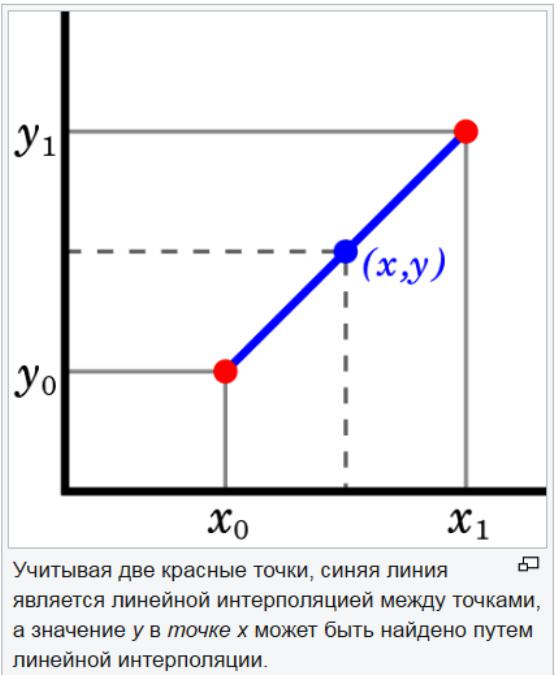
Strategija linearne interpolacije je korištenje ravne linije za povezivanje poznatih točaka vrijednosti s obje strane nepoznatog. Linearna interpolacija nije točna za nelinearne parametre. Ako se točke u skupu podataka promijene za veliku količinu, linearna interpolacija može dati pogrešnu procjenu.
Linearna ekstrapolacija može pomoći u procjeni vrijednosti koje su veće ili niže od vrijednosti u skupu podataka. Njegova je strategija koristiti podskup podataka umjesto čitavog skupa. Za ovu vrstu vrijednosti korisno je primijeniti metodu ekstrapolacije u predviđanju pomoću posljednje dvije ili tri točke za procjenu vrijednosti koja prelazi raspon podataka.
Polinomne i konične ekstrapolacije
Poznato je da tri točke daju jedinstveni polinom. Polinomna krivulja se može nastaviti nakon završetka takvih podataka. Obično se provodi Newtonovom metodom s konačnom razlikom ili korištenjem Lagrangeove interpolacijske formule. Polinom višeg reda treba ekstrapolirati s pažnjom, jer postoji velika mogućnost pogreške s polinomnom ekstrapolacijom. Ako se to dogodi, procjena pogreške povećava se eksponencijalno sa stupnjem polinoma.
U matematici, minimalna polinomna ekstrapolacija je transformacija slijeda koja se koristi za ubrzavanje konvergencije. Iako je Aitkenova metoda najpoznatija, ona često uspijeva, posebno za vektorske sekvence. U ovom se slučaju izvodi iteracija koja konstruira matricu. Njegovi su stupci razlike.

Primjerice, metoda ekstrapolacije koničnog presjeka može se izvesti pomoću 5 točaka označenih na kraju podataka. U slučaju da je stožasti presjek krug ili elipsa, tada će se petljati natrag i ponovno se ujediniti sa sobom. Parabola ili hiperbola se nikad ne sijeku. Ali mogu se saviti unatrag oko osi X. Ekstrapolacija konusa može se obaviti na papiru sa stožastim presjekom ili pomoću računala.
Metoda matematičke evaluacije
U ovoj metodi ekstrapolacije predviđa se vrijednost za bazno razdoblje. Dolje opisane radnje sustav automatski provodi i nisu vidljive korisniku. Ovaj je opis namijenjen pročišćavanju algoritma koji prikazuje očekivane vrijednosti iz količine pohranjene u sustavu i predviđa rezultat mjerenja brojila.
Ekstrapolacija pomoću definicije količine postupka izvodi se funkcijom: Yt = f (yi, t, aj).
Kao osnova za ekstrapolaciju dodaju se zaokruženi podaci tipičnog osnovnog razdoblja pohranjeni u rezultatima očitanja. Sustav određuje težinu Yt podataka vremenskih serija u t (vrijeme predviđenog razdoblja) kako bi se dobilo ispravno rješenje ekstrapolacijom. Tamo gdje su referentne točke uzete yi - razina niza i aj - parametar jednadžbe trenda.
Predviđanje značajki
Metoda fiksiranja statističke krivulje primjenjiva je na predviđanje funkcionalnosti.Statistički postupci odgovaraju prošlim podacima jedne ili više matematičkih funkcija, poput linearne, logaritamske, Fourijeve ili eksponencijalne. Najbolji su odabrani statističkim testom. Tada se ta prognoza ekstrapolira iz te matematičke veze metodom matematičke ekstrapolacije. Jedan od najjednostavnijih načina dobivanja grubih procjena budućih (ili prošlih) uvjeta je ekstrapoliranje podataka koji se s vremenom mijenjaju.
Na primjer, ako trebate napraviti grubu procjenu budućih razina onečišćujućih tvari u pitkoj vodi za 20 godina unaprijed, možete ekstrapolirati taj trend u posljednjih 20 godina. Isto se primjećuje ako u budućnosti trebate procijeniti učestalost pušenja ili raka pluća u pozadini. Prognoza se može izračunati trendovima posljednjih godina. Ekstrapolacija ove vrste može se izvesti manje složenim metodama. U mnogim se slučajevima (posebno u područjima marketinga i upravljanja poslovanjem) metoda ekstrapolacije tradicionalno koristi, na primjer, pregledom najnovijih podataka i intuitivnim procjenom onoga što se misli u budućnosti.
Metode utemeljene na pravilima također se mogu koristiti primjenom skupa unaprijed definiranih načela ili očekivanja koja se temelje na preliminarnom razumijevanju sustava i uzimanjem u obzir najnovijih podataka za tumačenje budućih događaja.
Uz bilo koju ekstrapolacijsku metodu, oprez je važan zbog prisutnosti brojnih nesigurnosti. Svaki postupak ekstrapolacije temelji se na pretpostavci da su dostupni pouzdani podaci o prošlim podacima i znanju. Slijedom toga, budućnost je određena istim faktorima koji su djelovali ranije.
Pogreške predviđanja
Zabluda ekstrapolacije (točnije pogrešna neopravdana ekstrapolacija) događa se kada se fenomen odgovoran za brojne trivijalne lokalne efekte čita kao velike globalne pojave. Drugi je razlog pogreške to što se ponekad generalizirana pravila izvode iz premalo činjenica. Dakle, Darwinova teorija evolucije fantastičan je primjer primjene metode ekstrapolacije u kojoj se objavljuju mehanizmi slučajnih promjena i prirodne selekcije da bi se uzeo u obzir razvoj tako složenih struktura poput sisavca ili imunološkog sustava živih organizama.
Pri pokušaju tumačenja rezultata istraživanja, znanstvenik treba izbjegavati ekstrapolaciju izvan raspona podataka i biti svjestan osnovnih pretpostavki kako bi izbjegao prihvaćanje nevaljanih zaključaka. Općenito, ekstrapolacija je legitimno znanstveno sredstvo. Dva su aspekta koja pomažu razlikovati valjanu i pogrešnu ekstrapolaciju. Vjerojatnost pogrešne ekstrapolacije veća je kada su za njenu konstrukciju dobiveni nedostatni podaci.
Statistički alati Excel
Da biste pronašli povezanost između godina i rezultata (na primjer, u poduzeću), možete koristiti Excel.
Za ove zadatke koriste se statistički alati za ekstrapolacijsko modeliranje koji su ugrađeni u sve verzije Excela, počevši od 97. Postupak:
- Unesite poznate vrijednosti, na primjer, ukupnu prodaju za 2016-2017, ako ih trebate odrediti za 2018. i 2020. godinu.
- Instalirajte analizu, značajku koja zahtijeva upotrebu dodatka.
- Da biste ga instalirali, izdvojite iz izbornika "Alati", "Dodaci".
- Provjerite prozor uslužnog programa za analizu i potvrdite sa "OK".
- Izmjerite korelacije između dviju serija.
- Ekstrapolacija koju je potrebno obaviti ima smisla samo ako postoji jasan trend (povezanost) između dva skupa brojeva (godina i prodaja) metodom ekstrapoliranja trendova.
- Za mjerenje ove korelacije koristite izbornik "Alati", "Alat za analizu".
- Na popisu "Alati za analizu" odaberite "Analiza korelacije" i kliknite "U redu".
- U polje Ulazni raspon unesite analizirani raspon, na primjer A6: B18, Excel će dodati simbol "$".
- U području "Izlazne mogućnosti" provjerite raspon izlaza i unesite ga u susjedno polje.
- Potvrdite s OK.
- Excel stvara niz od dva reda u dva stupca. Pronađite izračunatu vrijednost (na primjer, 0,981). Budući da je ta vrijednost blizu 1, to znači da postoji jaka povezanost između godina i podataka o prodaji. Ako korisnik primi vrijednost blizu nule, to će značiti da se trend ne pojavljuje. U ovom slučaju ekstrapolacija nema smisla.
- Započinje evaluacija budućih vrijednosti.
- Odaberite željeni raspon i kliknite gumb "Čarobnjak za grafikone".
- Odaberite grafikon (na primjer, oblaci točaka) i kliknite Finish.
Upotreba pokretnih prosjeka
Ove dvije ekstrapolacijske metode uključuju široku upotrebu podataka o prodaji kako bi se predviđala budućnost. Pomična prosječna vrijednost uzima niz podataka i "izglađuje" fluktuacije u njima. Cilj je izvući ekstremnost podataka iz razdoblja u razdoblje. Pomični prosjeci često se izračunavaju kvartalno ili tjedno. Za predviđanje budućih vrijednosti ekstrapolacija uključuje korištenje trendova utvrđenih povijesnim podacima. Glavna pretpostavka ekstrapolacije je da će se uzorak nastaviti u budućnosti, osim ako stvarni dokazi ne pokazuju drugačije. Da biste detaljnije razumjeli ove metode, možete razmotriti grafikon koji prikazuje prodaju gadgeta za velike tvrtke od 2012. do 2015. godine.
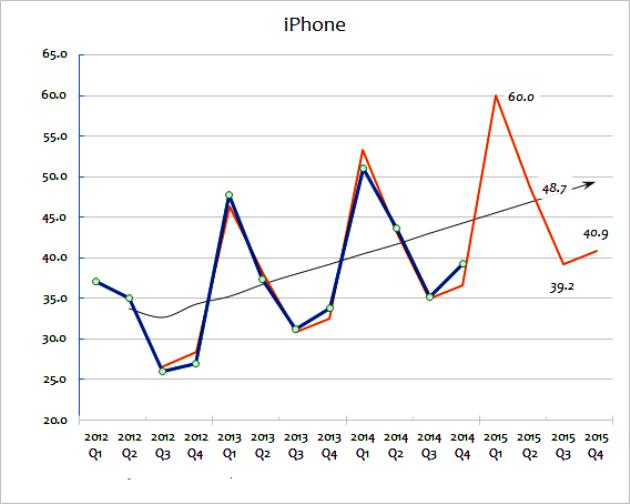
Ova metoda ekstrapolacije proračuna pokazuje stvarni iznos prodaje. Kao što vidite, ukupna količina prodaje varira iz godine u godinu, iako možete pretpostaviti (gledajući podatke) da postoji opći trend rasta prodaje. Crna crta pokazuje pomični prosjek. To se izračunava zbrajanjem posljednjih godina prodaje (npr. Q1 + Q2 + Q3 + Q4), a zatim dijeljenjem s četiri.
Ova metoda izglađuje godišnje promjene i daje dobru predstavu o općem trendu u godišnjoj prodaji. Pomični prosjek pomaže ukazivanju na trend rasta, izražen u postocima. Upravo će se ta ekstrapolacija prvi upotrijebiti za predviđanje buduće prodaje. To se matematički može učiniti pomoću proračunske tablice. Alternativno, ekstrapolirani trend jednostavno se može nacrtati na grafikonu kao gruba procjena.
Korelacija trendova
Uvijek je jedna tehnologija preteča druge. To se događa kada napredak u tehnologiji prekursora može biti usvojen sljedbenom tehnologijom. Kad postoje takvi odnosi, znanje o promjenama u tehnologiji prethodnika može se upotrijebiti za predviđanje napretka sljedbenika u budućnosti. Osim toga, ekstrapolacija prekursora omogućava predviđanje nastavka slijeđenja izvan vremenskog odgađanja.
U ovom se slučaju koristi metoda ekstrapolacije trendova u kojoj se, primjerice, uspoređuju trendovi u brzini vojnih i transportnih zrakoplova. Drugi primjer predviđanja korelacije trendova je predviđanje veličine i snage budućih računala na temelju napretka u mikroelektronskoj tehnologiji. Ponekad tehnologija sljedbenika ovisi o nekoliko tehnologija prethodnika, ali ne i o jednom prethodniku.
Fiksne kombinacije prethodnika mogu utjecati na promjenu niza, ali češće kombinacije nisu fiksne, a ulazi prethodnika razlikuju se i u kombinaciji i u snazi. Na primjer, može doći do povećanja brzine zrakoplova zbog poboljšanja motora, materijala, kontrola, goriva, aerodinamike i različitih kombinacija ovih faktora.
Primjer korelacijske prognoze dobiven ekstrapoliranjem trendova: ukupni putnički kilometri, ukupne zemljopisne milje i prosječna snaga slijetanja.Ekstrapolacija statistički utvrđenih trendova omogućava objektivan pristup prognoziranju. Međutim, ovaj pristup ima ozbiljna ograničenja i zamke. Bilo kakve pogreške ili pogrešni odabiri prilikom određivanja povijesnih podataka odrazit će se u prognozi, što smanjuje njezinu vrijednost.
Aplikacije, atributi i ograničenja
Metoda ekstrapolacije pripada području predviđanja. Predlaže da se obrasci koji su postojali u prošlosti nastave i u budućnosti, te da su ti obrasci pravilni i mogu se mjeriti. Drugim riječima, prošlost je dobar pokazatelj budućnosti. Aplikacije su korisne za razvijanje osnovnih podataka.
Atributi i ograničenja su jednostavni i jeftini alati za proračun, kao i složeni teorijski modeli.
- Procesni podaci - grafikoni i promatranja.
- Ključno je imati dobru bazu podataka i razumijevanje strukture unutar nje.
- Tehnika je najbolje uklapanje, omjer i tako dalje.
Privremeni standardni statistički postupci ne dovode do točnog odabira trendova koje prognostičar može udobno ekstrapolirati, izvodeći prognozu ekstrapolacijom. U takvim slučajevima prognostičar može prilagoditi statističke rezultate koristeći prosudbu. Također može u potpunosti zanemariti statistiku i ekstrapolirati čitav trend na temelju prosudbe.
Ovako stvorena predviđanja manje su točna od statističkih predviđanja, ali nisu nužno i nezadovoljavajuća. Jedan primjer takve ekstrapolacije trenda kvalitete je predviđanje složenosti zrakoplova. Pokušaji kvantificiranja ovog trenda nisu bili uspješni. Ali postotak pomičnih ili podesivih dijelova zrakoplova ekstrapoliran je frekvencijom s kojom su takvi elementi uvedeni u prošlosti. Te su prognoze bile prilično točne.
Specifične tehničke promjene se ne mogu predvidjeti na taj način, ali stupanj promjene mogu. Ovo pruža korisne materijale za planiranje, što ukazuje na trend u prošlom ponašanju.
