"Stohastička" je riječ koju fizičari, matematičari i drugi znanstvenici koriste kako bi opisali procese koji imaju element slučajnosti. Podrijetlo mu je starogrčki. Prevedeno, znači "u stanju pogoditi".
Značenje riječi "stohastički"

"Stohastički" je pojam koji se koristi u mnogim različitim područjima znanosti. Znači slučajnost, slučajnost, nesigurnost nečega. U etici Aristotela (njegov skulpturalni portret predstavljen je gore) koncept „stohastičkog“ je definicija koja se odnosi na sposobnost pogađanja. Očigledno, matematičari su ga koristili na osnovu toga što se element slučajnosti pojavljuje baš kad je potrebno pogoditi. Riječ "stohastički" pojam je koji se u Novom međunarodnom rječniku definira kao "pretpostavljen".
Dakle, može se primijetiti da tehničko značenje ovog pojma ne odgovara točno njegovom rječničkom (leksičkom) značenju. Neki autori koriste izraz "stohastički proces" kao sinonim za pojam "slučajni proces".
Stohastičnost u matematici

Upotreba ovog izraza u matematici trenutno je rasprostranjena. Na primjer, postoji takav koncept u teoriji vjerojatnosti kao stohastički proces. Njegov se rezultat ne može odrediti početnim stanjem ovog sustava.
Upotreba matematike u konceptu "stohastičnosti" pripisuje se djelima Vladislava Bortskevicha. On je taj izraz upotrijebio u značenju "iznio hipoteze". U matematici, posebno u takvom dijelu ove znanosti kao što je teorija vjerojatnosti, polje slučajnih istraživanja igra važnu ulogu. Na primjer, postoji takva stvar kao stohastička matrica. Stupci ili redovi ove matrice zbrajaju jedan.
Stohastička matematika (financijska)
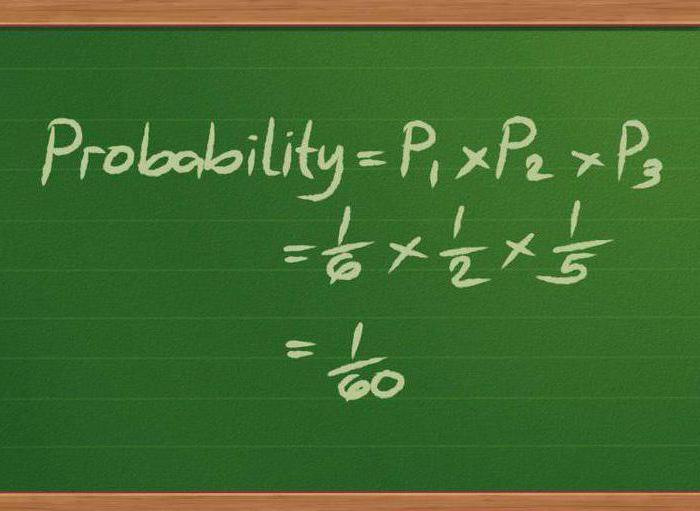
Ovaj odjeljak matematike analizira financijske strukture koje djeluju u uvjetima nesigurnosti. Osmišljen je da pronađe najracionalnije metode upravljanja financijskom imovinom i strukturama, uzimajući u obzir čimbenike poput stohastičke evolucije, rizika, vremena itd.
U znanosti je uobičajeno razlikovati sljedeće strukture i predmete koji se koriste u financijskoj matematici u cjelini:
- tvrtke (na primjer, tvrtke);
- pojedinci;
- posredničke strukture (mirovinski fondovi, banke);
- financijska tržišta.
Glavni predmet proučavanja stohastičke financijske matematike je upravo posljednji od njih. Ovaj se odjeljak temelji na disciplinama kao što su statistika slučajnih procesa, teorija slučajnih procesa itd.
Trenutno, čak i ljudima daleko od znanosti, iz brojnih vijesti i publikacija u medijima dobro je poznato da se vrijednosti takozvanih globalnih financijskih indeksa (na primjer, Dow Jones indeks) cijene dionica mijenjaju nasumično. L. Bachelier je prvi pokušao opisati pomoću matematike razvoj cijena dionica. Njegova stohastička metoda temelji se na teoriji vjerojatnosti. Disertacija L. Bacheliera koja predstavlja ovaj pokušaj objavljena je 1900. godine. Znanstvenik je dokazao formulu koja je trenutno poznata kao formula fer vrijednosti za opcije poziva. Odraz je stohastičke vjerojatnosti.
Važne ideje koje su nakon toga dovele do nastanka učinkovite tržišne teorije predstavljene su u radu M. Kendall, objavljenom 1953. Ovaj rad bavi se dinamikom cijena dionica. Istraživač to opisuje koristeći stohastičke procese.
Stohastičnost u fizici
Zahvaljujući fizičarima E. Fermiju, S. Ulamu, N. Metropolisu i D.Neumann se široko koristi Monte Carlo metoda. Ime joj dolazi od kazina smještenog u istom gradu u zemlji poput Monaka. Ovdje je stric Ulam posudio novac za igru. Korištenje prirode ponavljanja i šansi za proučavanje procesa slično je onome što se događa u kasinu.

Kod primjene ove metode modeliranja prvo se traži vjerojatni analog. Prije toga modeliranje je provedeno u suprotnom smjeru: korišteno je za provjeru rezultata ranije dobijenih determiniranih problema. Iako su slični pristupi postojali i prije otkrića metode Monte Carlo, oni nisu bili popularni i općeniti.
Enrico Fermi 1930. primijenio je stohastičke tehnike za izračunavanje svojstava neutrona, koja su tek otkrivena u to vrijeme. Monte Carlo metode kasnije su korištene tijekom rada na projektu Manhattan, iako su u to vrijeme mogućnosti računala bile značajno ograničene. Iz tog razloga, oni su postali rašireni tek nakon što su se pojavila računala.
Stohastički signali
Redoviti i stohastički signali imaju različite valne oblike. Ako ponovno izmjerimo potonje, dobivamo oscilacije koje imaju novi oblik, različit od prethodnog, ali pokazuju određenu sličnost u bitnim značajkama. Primjer stohastičkog signala je snimanje oscilacija morskih valova.
Zašto je potrebno razgovarati o tim prilično neobičnim signalima? Činjenica je da su u istraživanju automatskih sustava oni čak i češći nego što se predviđalo.
Stohastičnost i umjetna inteligencija
Programi stohastičke umjetne inteligencije djeluju pomoću vjerojatnih metoda. Algoritmi poput stohastičke optimizacije ili neuronske mreže mogu se navesti kao primjer. Isto se odnosi na simulirane algoritme žarenja i genetičke algoritme. U svim tim slučajevima stohastičnost može biti sadržana u problemu kao takvom ili u planiranju nečega pod uvjetom neizvjesnosti. Determinističko okruženje za sredstvo za modeliranje je jednostavnije od stohastičkog.

Dakle, kao što vidimo, pojam koji nas zanima koristi se u mnogim područjima znanosti. Naveli smo i okarakterizirali samo glavna područja njegove primjene. Studija svih tih procesa, vidite, vrlo je važna i relevantna. Zato će se pojam koji nas zanima vjerojatno još dugo koristiti u znanosti.








