Rahankertoja: määritelmä, ominaisuudet, olemus ja tyypit

Rahan tarjonnan määrään vaikuttavat aina monet tekijät. Ensimmäinen on ei-pankki- ja kotitaloussektorilla toimivien yritysten käyttäytyminen. Toiseksi kaupalliset pankit, jotka kykenevät käyttämään luottorahoja ei täysin, toisin sanoen eivät anna niitä lainoina, vaan jättävät syntyneet ylimääräiset varaukset kotona. Tällöin talletusten määrän muutokseen liittyy kertoimen vaikutus. Yritetään laskea rahakerroin.

Peruskäsitteet

Jotta ymmärrät mitä käsitteen "rahakertoja" ydin koostuu, sinulla on oltava käsitys kahdesta normista: varaus ja talletus.

Varanto-osuus osoittaa varantojen määrän suhteen pankkiin talletettujen talletusten osuuteen varantojen määränä tai talletusten arvosta:

rr = R / D.

Talletusaste määritellään käteissuhteena talletuksiin:

cr = C / D.

Se osoittaa, mihin väestö on taipuvaisempi: pitämään säästönsä käteisellä tai talletuksilla.

Tästä seuraa, että rahakerroin, tai kuten taloustieteilijät kutsuvat sitä, rahapohjakerroin on kerroin, joka ilmaisee kuinka monta kertaa rahan määrää kasvatetaan (vähennetään), kun rahamäärää kasvatetaan (vähennetään) yhdellä.

Kuten kaikki taloudelliset kertoimet, raha voi toimia myös molempiin suuntiin. Jos maan keskuspankki aikoo kasvattaa rahamäärää, se kasvattaa rahapohjaa, muuten se vähenee.

Rahan tarjonnan kertoin on riippuvainen yllä kuvatuista normeista. Jos talletusaste nousee, niin kertoin pienenee vastaavasti. Toisaalta varantoprosentin nousu (ts. Pankkitalletuksen osuuden kasvu varannon muodossa) vähentää kertoimen arvoa.

teoriassa,

Taloudellisessa teoriassa määrätään, että rahakerroin on yhtä suuri kuin kaupallisten luottolaitosten varantojen käänteiskurssin arvo, joka on pakollista varastointia keskuspankissa. Käytännössä se lasketaan raha-aggregaatin M osamääränä₂ rahapohjaan. Rahan määrän kertoimen dynamiikkaa on tutkittava maan rahan tarjonnan ja inflaatioprosessien hallitsemiseksi. Rahankertoja pystyy osoittamaan rahan tarjonnan mahdollisen kasvun ilman negatiivisia seurauksia nousevien kuluttajahintojen ja inflaation muodossa. Rahankertoimen laskentakaava on yksinkertainen, se on aina enemmän kuin yksi.

käytännössä

Lauseke kertoimen laskentaan voidaan johtaa käyttämällä varausastetta: rr = R / D ja talletuskorkoa: cr = C / D.

Koska C = cr x D ja R = rr x D, saamme yhtälöt:

M = C + D = cr x D + D = (cr + 1) x D

ja

H = C + R = cr x D + rr x D = (cr + rr) x D.

Jaa nyt ensimmäinen tasa-arvo toiseksi:

M / H = ((cr + 1) x D (cr + 1)) / (cr + rr) x D (cr + rr) = (cr + 1) / (cr + rr)

Saadaan yhtälö: M = ((cr + 1) / (cr + rr)) x H,

täältä:

M = mult_den x H mult_den = (cr + 1) / (cr + rr).

Rahankertoja on lauseke (cr + 1) / (cr + rr).

Jos oletetaan, että C = 0 (eli ei ole rahaa), ja poistumatta pankkijärjestelmästä rahan tarjonta pyörii, kertoja muuttuu pankiksi: mult_D = 1 / rr. Ehkä siksi pankkikertojaa kutsuttiin yksinkertaiseksi rahankertoimeksi.

Rahan kertoimen ydin

Se koostuu mekanismista, jolla kasvatetaan rahamäärää pankkien asiakkaiden avaamien talletusten takia, siirtämällä ei-käteisvarojen liikkumista valtioista riippumattomien pankkien järjestelmän kautta.

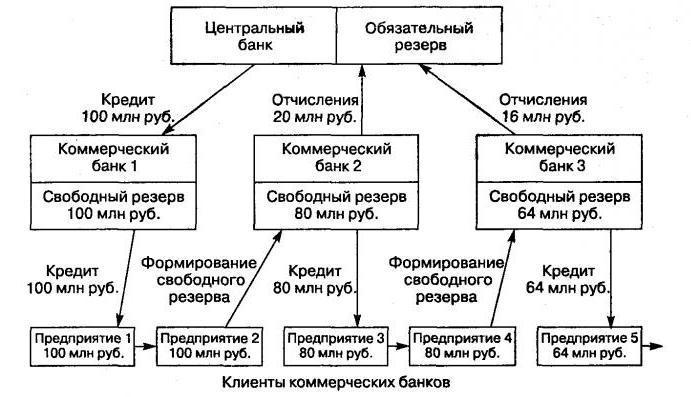
Tämä mekanismi luodaan edellyttäen, että on olemassa kahden tason pankkijärjestelmä. Päästöprosessi tapahtuu tässä tapauksessa keskuspankin (käteisvarojen liikkeeseenlasku) ja liikepankkijärjestelmän (käteisvarojen liikkeeseenlasku) välillä.

Pankkienvälisessä liikkeessä olevan rahan määrän kasvu (rahan kertomisprosessi) johtuu pankkien myöntämistä lainoista, jotka houkutellaan asiakkaiden varojen talletustilille, joita ne käyttävät suorittaessaan erilaisia ​​maksuja ja maksutapahtumia. Toisaalta lainanottavien pankkien asiakkaat voivat avata talletuksia kolmansien osapuolien pankeissa. Näin ollen talletusten kokonaismäärä koko pankkijärjestelmässä ylittää melkein aina alun perin luodun talletuksen määrän.

Animaation periaate

Jokaisella maalla on omat erityispiirteensä jakelupankkijärjestelmissä. Esimerkiksi valtioissa, joissa komento- ja jakelutalous tapahtuu, päästöt suoritetaan ylhäältä alemman direktiivin mukaisesti. Maissa, joissa markkinat ovat normaalit, pankkijärjestelmä toimii kahdella tasolla: keskuspankilla ja liikepankkikerroksella. Siksi päästöillä sellaisessa järjestelmässä on animaatio.

Hallitsemalla tätä mekanismia asianmukaisesti, keskuspankilla on mahdollisuus laajentaa tai kaventaa koko liikepankkien laitoksen päästöprosesseja. Taloudellisesta teoriasta käy selvästi ilmi, että kokonaistuotannon kasvukerroin (lasku) rahamäärän (tarkemmin sen yksikön) saamiseksi on kerroin. Tämä arvo osoittaa, kuinka monta kertaa tarjonta voi muuttua (kasvaa tai vähentyä) talletusten määrän lisääntymisen tai vähentymisen jälkeen rahoitus- ja luottosektorilla.

Rahapohja ei ole muuta kuin kaupallisten pankkien suorittamat pakolliset varaukset ja käteisellä liikkeessä olevat käteisvarat, jotka ovat keskuspankin valvonnan ulkopuolella. Kun otetaan huomioon rahankertoimen kerroin kuvatuissa näkökohdissa, voimme johtaa kaavan:

M - 1 / r

M = (1 + c) / (r + e + c).

Tässä ”c” tarkoittaa käteissuhdetta kaikissa maan pankkijärjestelmässä olevissa talletuksissa, “r” tarkoittaa pakollista varantoa ja “e” osoittaa käytettävissä olevien pankkivarantojen suhdetta talletuksiin.

Indikaattorin arvo

Keskuspankki säätelee mekanismia rahan määrän lisäämiseksi (vähentämiseksi) pakollisilla varannonkeruuilla kussakin liikepankissa. Rahankertoimen arvo ei ole paikallaan. Se vaihtelee paitsi tilassa ja ajassa, myös maasta toiseen. Maissa, joissa taloudet ovat kehittyneet, tämä arvo voi olla yli kaksi kertaa suurempi kuin ensimmäisen liikkeeseenlaskun arvo.

Johdanna kaava

Rahankertoja (kaava kuvataan alla) on helppo laskea:

m = rahan tarjonta / rahapohja = M / B.

Prosessissa, jossa keskuspankki säätelee rahankertoimen (k) arvoa, syntyy rahapohjan käsite. Se perustuu keskuspankin hallussa oleviin liikepankkien talletuksiin, ja likvidein raha on käteistä.

Rahatalli = M₀ + vaadittavien varantojen rahatarjonta (CB) + rahoitustarve kirjeenvaihtotileille kaupallisten rahoituslaitosten verkoston keskuspankissa.

Rahatarjonta osoittaa rahan määrän, jota maan keskuspankki voi käyttää:

Rahan tarjonta = perusta • kerroin.

Tämän kaavan perusteella voimme määrittää rahankertoimen: tämä on rahan tarjonnan suhde (M₂) rahapohjaan.

Keskuspankin tileillä olevien kaupallisten finanssilaitosten varantojen määrän ja rahankertoimen arvon välillä on kääntäen verrannollinen suhde. Ja jos rahakerroin laskee, liikepankkien vakuuttamien varantojen määrä nousee. Jos rahakerroin kasvaa, ei-käteisvarojen liikevaihto kasvaa (verrattuna käteiseen), koska rahapohjakertoimen kasvu liittyy suoraan käteisvarojen ja kirjeenvaihtajatilien saldon kasvuun keskuspankissa.

Rahankertoimen riippuvuus

Kuten jo mainittiin, rahankertoimen koko riippuu varaus- ja talletusnormeista. Mitä korkeammat ne ovat, sitä suurempi vahingoittumattomien varastojen määrä. Mitä suurempi käteissuhde massissa on, että väestö ei kiirehti sijoittamaan talletuksiin, sitä alhaisempi on kertoimen arvo. Tämä on selvästi näkyvissä kaaviossa.

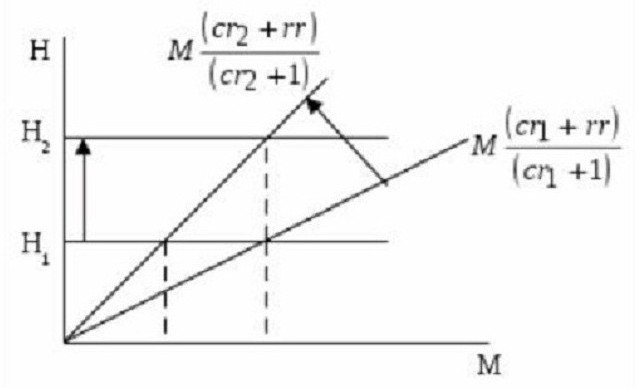
Se heijastaa rahapohjan (N) suhdetta rahasumman (M) ja kertoimen kautta, joka on yhtäsuuri (cr + 1) / (cr + rr). Tämä osoittaa, että kallistuskulman tangentti on yhtä suuri kuin suhde (cr + rr) / (cr + 1).

Jos H₁ (rahapohjan arvo) ei muutu, niin talletusnopeuden kasvu r: stä₁ cr₂ vähentää rahankertoimen määrää ja lisää samalla käyrän kaltevuutta heijastaen rahan tarjontaa (tai rahan tarjontaa). Seurauksena on, että juuri tämä lause vähennetään arvosta M₁ M: lle₂. Jos on tarpeen, että rahan tarjonta (tai tarjonta) ei muutu rahankertoimen laskiessa, vaan on vakaa tilassa M₁, Keskuspankin tulisi nostaa rahapohja arvoon N₂.

Edellä esitetystä on selvää: talletuskoron nousu vähentää rahan kertoimen arvoa. Toisaalta voidaan todeta, että varantoprosenttimäärä nousee (varantoina pidettyjen talletuksien osuus kasvaa). Toisin sanoen, kun pankkien ylimääräiset varannot (joita ei myönnetä lainaksi asiakkaille) lisääntyvät, rahakertoimen arvo laskee.

Rahankertoja

Tämä on taloudellinen kerroin, joka kuvaa pankkien varantojen ylittymistä (tai vähennyksiä). Se muodostuu uusien talletusten (käteisvarojen) luomisen seurauksena. Ne ilmenevät myöntäessään lainoja asiakkaille lisävapaista varauksista, jotka pankki on vastaanottanut ulkopuolelta.

Tästä käy selväksi: luottolähteet, jotka jättivät yhden liikepankin liikkeeseen lasketuina lainoina, muuttuvat toisen pankin omaisuudeksi. Ja hän puolestaan ​​tarjoaa asiakkailleen tämän rahan, vain käteisellä. Toisin sanoen yhden kaupallisen rahoitus- ja luottolaitoksen liikkeeseen laskema rahayksikkö luo luottovarannon toiselle pankille.

Liikepankkien varanormit

Pankin kykyä luoda ylimääräisiä varantoja rajoittaa toiminto muodostaa vaadittavat varannot liikepankkien rakenteella. Niiden määrät määräytyy varannonormilla, jonka säännöt määritetään lailla. Keskuspankki laskee ne prosentteina pankkien veloista. Nämä varannot auttavat maan pankkijärjestelmää tarjoamaan likviditeettiä epäsuotuisina ajanjaksoina ja säätelemään liikkeessä olevan rahan tarjontaa:

M = 1 / Rn, missä Rn on varanormi.

Lasketaan rahakerroin, jotta voidaan laskea koko rahasumma, joka voidaan luoda yhdellä ylimääräisen varannon rahayksiköllä tietyllä varantokurssilla:

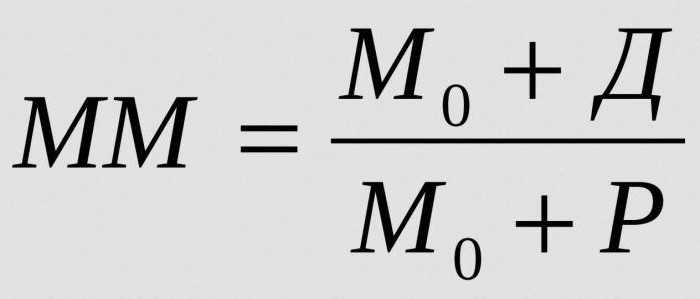
missä:

• MM - rahakerroin tietyllä ajanjaksolla;
• M₀ - rahan tarjonta pankkikierroksen ulkopuolella
• D - liikepankkien talletuksiin tallennetut rahamäärät;
• R - kirjeenvaihtotileillä ja kassalla olevat kaupallisten pankkien varannot.

Rahamarkkinoiden vakaa tasapaino voidaan ravistaa lisääntyneellä rahakertoimella. Ja jopa provosoida inflaatiota.

Mistä pankkikertoja riippuu?

Rahakertoimen suuruus riippuu seuraavista tekijöistä:

• varantovelvoite kaupallisille pankeille;
• väestön ja yritysten lainakysynnän vähentyminen ja lainakorkojen samanaikainen nousu, mikä yleensä tarkoittaa lainojen myöntämisen ja talletusten määrän vähentymistä;
• Pankkien käyttämien varojen käyttö kolmansien osapuolten käteismaksutapahtumiin, mikä aiheuttaa animaatioprosessin keskeyttämisen ja vähentää sen arvoa.
• Asiakastilille saatujen kassavarojen lisääntyminen tai varojen osuuden myynti pankkienvälisillä markkinoilla luo yleensä olosuhteet kertoimen kasvulle.