L’essència i els mètodes d’extrapolació

La paraula composta "extrapolació" està composta per dues paraules simples. La primera en llatí sona extra i significa "fora", "per", "fora". El segon del mateix llatí sona polire i significa "canviar", "endreçar", "suau". En general, l'extrapolació es pot definir com un valor fora de dos punts donats. Es considera una valoració del que s’extreu de fets coneguts que amplien dades en una zona desconeguda per arribar al resultat previst. Aquest concepte també es pot atribuir a la predicció de la imatge del futur, assumint la veritat de les tendències presents i passades.

El mètode d'extrapolació suposa que les dades o observacions en el futur continuaran sent similars. Així, es poden predir resultats futurs. Es pot considerar com una hipòtesi matemàtica. L’extrapolació utilitza dades i fets d’una situació concreta i proporciona prediccions sobre què pot passar al final.

Historial d’extrapolació

Aquest mètode s’anomena sovint com a extrapolació de Richardson o el mètode de Romberg. Però això no és del tot correcte, ja que durant segles hi ha hagut mètodes numèrics similars per resoldre aquests problemes. Per tant, la famosa Richardson h2 (extrapolació per a una solució numèrica) no és la primera. Un mètode similar es va aplicar en els càlculs de Huygens ja des del 1654. El mateix terme "extrapolació" va ser inventat per Thomas D. Clareson per primera vegada el 1959 en un llibre sobre ciència i ficció.

Els mètodes d'extrapolació es poden entendre com a extensió de dades o processos, cosa que suggereix que un procés similar s'aplicarà fora d'ells. L’extrapolació és un concepte important emprat no només en matemàtiques, sinó també en altres àrees, com la sociologia, la psicologia, la predicció. Per exemple, un conductor sol extrapolar les condicions de conducció fora de la seva visió. L'extrapolació es pot atribuir a un mètode en què els valors de les dades es tracten com a punts x1, x2 ..., xn, i el valor s'aproxima al límit d'un rang de punts determinat.

Beneficis d'ús:

1. Un mètode de predicció senzill.
2. No es requereixen moltes dades.
3. Analítiques ràpides i econòmiques.

El mètode existeix en estadístiques. Si s'eliminen periòdicament qualsevol valor, la resposta s'aproxima al següent punt de dades. Un exemple de mètode d'extrapolació és una previsió meteorològica, que examina el rerefons de les dades i extrapola el model previst del futur. Un exemple encara més senzill, si teniu informació sobre diumenges, dilluns i dimarts, podeu extrapolar dimecres o dijous.

Desavantatges d'utilitzar l'extrapolació:

1. Fiabilitat, si hi ha fluctuacions significatives en les dades històriques.
2. El supòsit que la tendència passada continuarà en el futur difícilment és possible en molts entorns empresarials competitius.
3. Ignora factors de qualitat, com ara canvis en els gustos i la moda.

Acceleració de seqüències

Els mètodes d'extrapolació són crear una línia tangent al final de les dades conegudes i expandir-la més enllà d'aquesta àrea. Igual que la interpolació, l'extrapolació utilitza molts mètodes que requereixen un coneixement previ del procés que crea els punts de dades existents. El mètode inclou extrapolació lineal i polinòmica, extremació cònica i corba francesa.

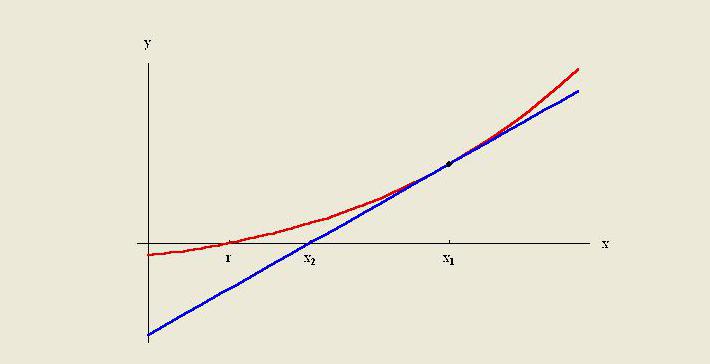
Per regla general, la qualitat d’un determinat mètode està limitada per supòsits sobre la funció. En anàlisi numèrica, l'extrapolació de Richardson és un mètode d'acceleració de seqüència utilitzat per millorar la taxa de convergència.Porta el nom de Lewis Fry Richardson. Va introduir la tècnica de càlcul a principis del segle XX, la utilitat dels quals per als càlculs pràctics difícilment es pot sobreestimar.

Les aplicacions pràctiques de l'extrapolació de Richardson inclouen la integració de Romberg, que s'aplica a la regla del trapezi i a l'algorisme de Bulliers-Stoehr per resoldre equacions diferencials ordinàries.

Mètode lineal

El mètode d'extrapolació lineal és útil quan s'especifica una funció lineal. Això es fa dibuixant una línia tangent al punt final d’un gràfic determinat i ampliant-la més enllà. Aquest mètode d'extrapolació en la previsió dóna bons resultats quan el punt a preveure no es troba massa lluny de les dades. La interpolació lineal és útil per trobar valors entre punts donats. Es pot considerar com "omplir els buits" de la taula de dades.

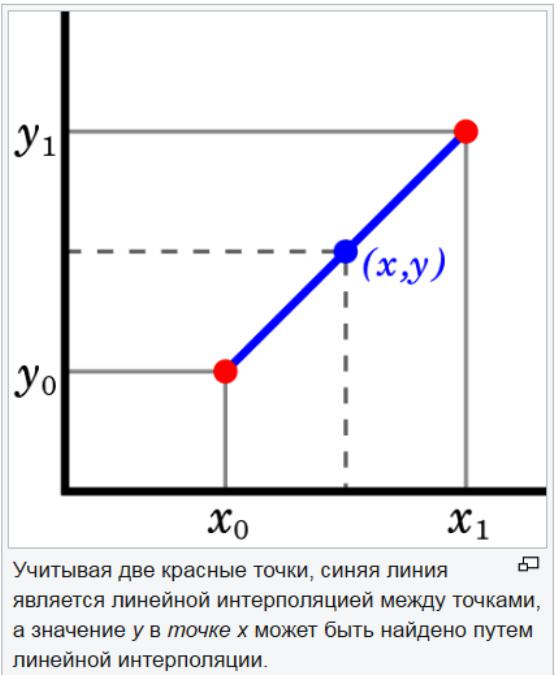
Una estratègia d'interpolació lineal és utilitzar una línia recta per connectar punts de valors coneguts a banda i banda de la incògnita. La interpolació lineal no és precisa per a paràmetres no lineals. Si els punts del conjunt de dades canvien en gran quantitat, la interpolació lineal pot donar una estimació incorrecta.

L’extrapolació lineal pot ajudar a estimar valors superiors o inferiors als valors del conjunt de dades. La seva estratègia és utilitzar un subconjunt de dades en lloc de tot el conjunt. Per a aquest tipus de valor, és útil aplicar el mètode d'extrapolació en la previsió utilitzant els dos o tres últims punts per estimar un valor superior a l'interval de dades.

Extrapolacions polinòmiques i còniques

Se sap que tres punts donen un polinomi únic. Es pot continuar amb una corba polinòmica després de la finalització d'aquestes dades. Generalment es porta a terme pel mètode de Newton amb una diferència finita o mitjançant la fórmula d'interpolació Lagrange. Un polinomi d’ordre superior s’hauria d’extrapolar amb la deguda cura, perquè hi ha una probabilitat d’error amb l’extrapolació polinòmica. Si això succeeix, l’estimació d’error augmentarà exponencialment amb el grau del polinomi.

En matemàtiques, l'extrapolació polinòmica mínima és una transformació de seqüència utilitzada per accelerar la convergència. Tot i que el mètode d’Aitken és més conegut, sovint falla, sobretot per a seqüències vectorials. En aquest cas, es realitza una iteració que construeix la matriu. Les seves columnes són diferències.

Per exemple, es pot fer un mètode d'extrapolació per a una secció cònica utilitzant 5 punts indicats prop del final de les dades. En cas que la secció cònica sigui un cercle o una el·lipse, es tornarà a fer un llaç enrere i es reunirà amb ella mateixa. La paràbola o la hipèrbola no s’entrellacen mai Però es poden doblar sobre l’eix X. L’extrapolació del con es pot fer sobre paper amb una secció cònica o mitjançant un ordinador.

Mètode d’avaluació matemàtica

En aquest mètode d'extrapolació, es preveu el valor del període base. Les accions descrites a continuació són realitzades automàticament pel sistema i no són visibles per a l'usuari. La descripció està destinada a perfeccionar l'algoritme, que mostra els valors esperats de la quantitat emmagatzemada al sistema i prediu el resultat de la mesura del mesurador.

L’extrapolació mitjançant la definició de la quantitat del procediment es realitza mitjançant la funció: Yt = f (yi, t, aj).

Com a base per a l'extrapolació, s'afegeixen les dades arrodonides d'un període base típic emmagatzemat als resultats de lectura. El sistema determina el pes Yt de les dades de sèries horàries en t (temps del període previst) per obtenir la solució correcta per extrapolació. Quan en el punt de referència es pren yi - el nivell de la sèrie i aj - el paràmetre de l'equació de tendència.

Predicció de funcions

El mètode de fixació d'una corba estadística és aplicable a la predicció de la funcionalitat.Els procediments estadístics corresponen a dades anteriors d’una o més funcions matemàtiques, com ara lineals, logarítmiques, de Fourier o exponencials. Els millors es seleccionen mitjançant un test estadístic. Llavors, aquesta previsió és extrapolada a partir d'aquesta connexió matemàtica pel mètode d'extrapolació matemàtica. Una de les maneres més fàcils d’obtenir estimacions aproximades de condicions futures (o passades) és extrapolar dades que canvien amb el pas del temps.

Per exemple, si necessiteu fer una avaluació aproximada dels nivells futurs de contaminants en aigua potable amb 20 anys d’antelació, podeu extrapolar aquesta tendència dels darrers 20 anys. El mateix s’observa si cal estimar la prevalença de fumar o càncer de pulmó en segon pla en un futur. Es pot fer una previsió calculant les tendències dels darrers anys. Les extrapolacions d’aquest tipus es poden fer mitjançant mètodes menys complexos. En molts casos (especialment en les àrees de màrqueting i gestió empresarial), el mètode d’extrapolació s’utilitza tradicionalment, per exemple, mitjançant la visualització de les darreres dades i l’avaluació intuïtiva del que s’entén en el futur.

Els mètodes basats en regles també es poden utilitzar aplicant un conjunt de principis o expectatives predefinits basats en una comprensió preliminar del sistema i tenint en compte les darreres dades per interpretar esdeveniments futurs.

Amb qualsevol mètode d’extrapolació, la precaució és important a causa de la presència de nombroses incerteses. Qualsevol procediment d'extrapolació es basa en el supòsit que hi ha informació fiable disponible en dades i coneixements anteriors. En conseqüència, el futur està determinat pels mateixos factors que van actuar anteriorment.

Errors de previsió

La fal·làcia de l'extrapolació (més precisament, la fal·làcia de l'extrapolació injustificada) es produeix quan el fenomen responsable d'una sèrie d'efectes locals trivials es llegeix com a grans fenòmens globals. Un altre motiu de l’error és que, de vegades, les regles generalitzades es dedueixen de massa pocs fets. Així, la teoria de l’evolució de Darwin és un exemple fantàstic de l’aplicació del mètode d’extrapolació, en què s’anuncien els mecanismes de canvis aleatoris i de selecció natural per tenir en compte el desenvolupament d’estructures tan complexes com la visió de mamífers o el sistema immune dels organismes vius.

Quan s’intenta interpretar els resultats de la investigació, el científic hauria d’evitar l’extrapolació fora del rang de dades i ha de ser conscient de les hipòtesis subjacents per evitar acceptar conclusions no vàlides. En general, l'extrapolació és una eina científica legítima. Hi ha dos aspectes que ajuden a distingir entre extrapolació vàlida i errònia. La probabilitat d'extrapolació errònia és més alta quan es van obtenir punts per a dades insuficients per a la seva construcció.

Eines estadístiques de l'Excel

Per trobar una correlació entre anys i resultats (per exemple, en una empresa), podeu utilitzar Excel.

Per a aquestes tasques, s’utilitzen eines estadístiques per al modelat d’extrapolació integrades a totes les versions d’Excel, a partir del 97. Procediment:

1. Introduïu els valors coneguts, per exemple, el total de vendes del curs 2016-2017, si voleu determinar-los per al 2018 i el 2020.
2. Install Analysis, una característica que requereix l’ús d’un complement.
3. Per instal·lar-lo, extreu del menú "Eines", "Complements".
4. Comproveu la finestra d’utilitat d’anàlisi i confirmeu amb “OK”.
5. Mesura correlacions entre dues sèries.
6. L’extrapolació que cal fer només té sentit si hi ha una clara tendència (correlació) entre els dos conjunts de nombres (anys i vendes) pel mètode d’extrapolar tendències.
7. Per mesurar aquesta correlació, utilitzeu el menú "Eines", "Utilitats d'anàlisi".
8. A la llista "Eines d'anàlisi", seleccioneu "Anàlisi de correlació" i feu clic a "D'acord".
9. Al camp d’entrada, introduïu l’interval analitzat, per exemple A6: B18, Excel afegirà el símbol "$".
10. A l’àrea “Opcions de sortida”, comproveu l’interval de sortida i introduïu-lo al camp contigu.
11. Confirmeu-ho amb D'acord.
12. Excel crea una matriu de dues files en dues columnes. Cerqueu el valor calculat (per exemple, 0.981). Com que aquest valor s’aproxima a 1, això vol dir que hi ha una forta correlació entre anys i xifres de vendes. Si l’usuari rep un valor proper a zero, això significarà que la tendència no es produeix. En aquest cas, l’extrapolació no té sentit.
13. S'inicia una avaluació de valors futurs.
14. Seleccioneu l’interval necessari i feu clic al botó “Assistent de gràfics”.
15. Seleccioneu un gràfic (per exemple, núvols de punts) i feu clic a Finalitzar.

L’ús de mitjanes mòbils

Aquests dos mètodes d'extrapolació impliquen l'ús generalitzat de dades de vendes per predir el futur. El valor mitjà mòbil pren una sèrie de dades i "suavitza" les fluctuacions en elles. L’objectiu és extreure l’extrema de dades de període en període. Les mitjanes mòbils sovint es calculen trimestralment o setmanalment. Per predir valors futurs, l'extrapolació implica l'ús de tendències establertes per dades històriques. El principal supòsit d'extrapolació és que la mostra continuarà en el futur, tret que l'evidència real indiqui el contrari. Per comprendre aquests mètodes amb més detall, podeu considerar un gràfic que mostra les vendes d’aparells per a grans empreses des del 2012 fins al 2015.

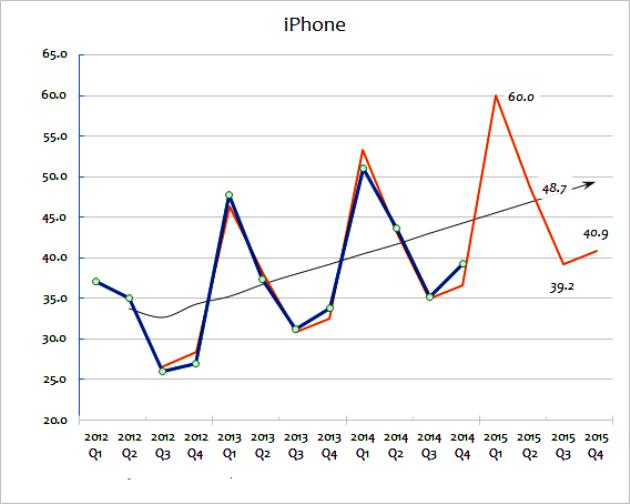
Aquest mètode d'extrapolació de càlcul mostra la xifra de vendes reals. Com podeu veure, la quantitat total de vendes varia d’any en any, tot i que es pot endevinar (mirant les dades) que hi ha una tendència general de creixement de vendes. La línia negra mostra la mitjana mòbil. Això es calcula afegint els darrers anys de vendes (per exemple, Q1 + Q2 + Q3 + Q4) i després dividint per quatre.

Aquest mètode suavitza els canvis anuals i dóna una bona idea de la tendència general de les vendes anuals. Una mitjana mòbil ajuda a indicar una tendència de creixement, expressada en percentatge. Aquesta extrapolació s’utilitzarà primer per predir el camí de les vendes futures. Es pot fer matemàticament mitjançant un full de càlcul. De forma alternativa, es pot simplement dibuixar una tendència extrapolada en un gràfic com a estimació aproximada.

Correlació de tendències

Sempre una tecnologia és la precursora d’una altra. Això succeeix quan els avenços aconseguits en tecnologia de precursors poden adoptar-los per part de la tecnologia seguidora. Quan existeixen aquestes relacions, el coneixement dels canvis en la tecnologia dels predecessors es pot utilitzar per predir el futur dels seguidors de la tecnologia en el futur. A més, l'extrapolació del precursor permet predir la continuació del seguiment més enllà del retard.

En aquest cas s’utilitza el mètode d’extrapolació de tendències, en el qual, per exemple, es comparen les tendències en la velocitat dels avions militars i de transport. Un altre exemple de previsió de correlació de tendències és predir la mida i la potència dels futurs ordinadors basats en els avenços de la tecnologia microelectrònica. De vegades, la tecnologia dels seguidors depèn de diverses tecnologies de precursors, però no d’un predecessor.

Les combinacions fixes de predecessors poden afectar el canvi de la seqüència, però més sovint les combinacions no són fixes i les entrades dels predecessors difereixen tant en combinació com en força. Per exemple, es pot produir un augment de la velocitat dels avions degut a la millora de motors, materials, controls, combustible, aerodinàmica i diverses combinacions d’aquests factors.

Un exemple de previsió de correlació obtinguda per l'extrapolació de les tendències: milles de passatgers totals, milles geogràfiques totals i potència d'aterratge mitjana.L’extrapolació de tendències estadísticament determinades permet un enfocament objectiu de la previsió. No obstant això, aquest enfocament té greus limitacions i entrebancs. Qualsevol error o elecció incorrecta que es faci en la determinació de dades històriques es reflectirà en la previsió, fet que redueix el seu valor.

Aplicacions, atributs i límits

El mètode d'extrapolació pertany al camp de la predicció. Suggereix que els patrons existents en el passat continuaran en el futur i que aquests patrons són regulars i es poden mesurar. En altres paraules, el passat és un bon indicador de futur. Les aplicacions són útils per desenvolupar dades de referència.

Els atributs i els límits són eines de càlcul senzilles i econòmiques, i també models teòrics complexos.

1. Processar dades: gràfics i observacions.
2. La clau és tenir una bona base de dades i comprendre l'estructura que hi ha dins.
3. La tècnica és la millor adequació, relació i així successivament.

Els procediments estadístics estàndard temporals no condueixen a una selecció precisa de les tendències que el pronòstic pot extrapolar amb comoditat, realitzant la previsió per extrapolació. En aquests casos, el pronòstic pot "ajustar" els resultats estadístics mitjançant judici. També pot ignorar per complet les estadístiques i extrapolar tota la tendència basada en el judici.

Les previsions generades d'aquesta manera són menys exactes que les previsions estadístiques, però no necessàriament insatisfactòries. Un exemple d'aquesta extrapolació d'una tendència de qualitat és predir la complexitat dels avions. Els intents de quantificar aquesta tendència no han tingut èxit. Però el percentatge de parts mòbils o ajustables de l'aeronau es va extrapolar amb la freqüència amb què es van introduir aquests elements en el passat. Aquestes previsions eren força exactes.

No es poden preveure canvis tècnics específics d'aquesta manera, però sí el grau de canvi. Això proporciona materials de planificació útils, cosa que indica una tendència del comportament passat.